Biot-Savart law

In physics, more particularly in electrodynamics, the law first formulated by Jean-Baptiste Biot and Félix Savart describes the magnetic induction B (proportional to the magnetic field H) caused by a direct electric current in a wire. Biot and Savart interpreted their measurements by an integral relation. Laplace gave a differential form of their result, which now often is also referred to as the Biot-Savart law, or sometimes as the Biot-Savart-Laplace law. By integrating Laplace's equation over an infinitely long wire, the original integral form of Biot and Savart is obtained.

Ørsted's discovery

Ørsted's experiment: A bar magnet is hung above a wire carrying the direct current i. The magnetic field B is in the direction of the turn of a screw driven into the direction of i. The magnet experiences a torque, the south pole moves toward the reader, the north pole away from the reader. See Ampere's rule.

Electricity and magnetism have been known since Antiquity. Rubbed amber was known to attract light objects, and lodestone (loadstone, magnetite) needles have been used as magnetic compasses since ca 1300 AD. However, the two phenomena, electricity and magnetism, were seen as unrelated. It required Alessandro Volta's invention of the battery ("Voltaic pile") before sustained electric currents of non-negligible strength could be generated. Soon after Volta's invention (during the spring of 1800), the Danish physicist Ørsted noticed in April 1820, while experimenting with the Voltaic pile, an effect of an electric current on a permanent magnet. He wrote a (Latin) publication which he sent round Europe. François Arago demonstrated the discovery at the French Académie des Sciences (11 September 1820), which inspired Jean-Baptiste Biot and André-Marie Ampère to investigate the effect further. At a meeting of the Académie des Sciences on 30 October 1820, Biot and Savart announced that the magnetic force exerted by a long conductor on a magnetic pole falls off with the reciprocal of the distance and is orientated perpendicular to the wire. Simultaneously they published this in a short note. Laplace generalized their result mathematically. Ampère also wrote about the effect in the very same year.

Although Ørsted himself could not have foreseen this, his very fundamental discovery led soon to the invention of the dynamo and the electric motor. The importance of these inventions cannot be exaggerated. To mention just one aspect: every western household today has a couple of dozen electromotors in and around the house.

Laplace's formula

Magnetic induction dB at point r due to infinitesimal piece ds (red) of wire (blue) transporting electric current i.

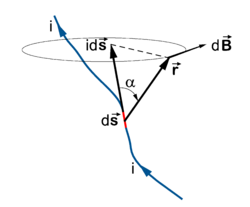
The infinitesimal magnetic induction $\scriptstyle d{\vec {\mathbf {B} }}$ at point $\scriptstyle {\vec {\mathbf {r} }}$ (see figure on the right) is given by the following formula due to Laplace,

$d{\vec {\mathbf {B} }}=k{\frac {id{\vec {\mathbf {s} }}\times {\vec {\mathbf {r} }}}{|{\vec {\mathbf {r} }}|^{3}}},$

where the magnetic induction is given as a vector product, i.e., is perpendicular to the plane spanned by $\scriptstyle d{\vec {\mathbf {s} }}$ and $\scriptstyle {\vec {\mathbf {r} }}$. The electric current i is constant in time. The piece of the wire contributing to the magnetic induction can be seen as a vector of infinitesimal length ds and with direction tangent to the wire. The constant k depends on the units chosen. In rationalized SI units k is the magnetic constant (vacuum permeability) divided by 4π. The magnetic constant μ₀ = 4π ×10⁻⁷ N/A² (newton divided by ampere squared). In Gaussian units k = 1 / c (one over the velocity of light).

If we remember the fact that the vector $\scriptstyle {\vec {\mathbf {r} }}$ has dimension length, we see that this equation is an inverse distance squared law.

Formula of Biot and Savart

Field B due to current i in infinitely long straight wire.

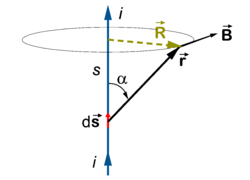
Take a straight infinitely long wire transporting the current i. Write, using R = rsinα (see the figure),

$d{\vec {\mathbf {s} }}\times {\vec {\mathbf {r} }}={\hat {\mathbf {e} }}\,r\sin \alpha \,ds={\hat {\mathbf {e} }}\,R\,ds,$

where $\scriptstyle {\hat {\mathbf {e} }}$ is a unit vector perpendicular to the plane spanned by the wire and the vector $\scriptstyle {\vec {\mathbf {R} }}$ perpendicular to the wire. Note that if $\scriptstyle d{\vec {\mathbf {s} }}$ is moved along the wire, all contributions from the segments to the magnetic induction are along this unit vector. Hence, if we integrate over the wire we add up all these contributions, so that

${\vec {\mathbf {B} }}={\hat {\mathbf {e} }}\,iRk\int _{-\infty }^{\infty }{\frac {ds}{(s^{2}+R^{2})^{3/2}}}$

where, by the Pythagorean theorem,

$|{\vec {\mathbf {r} }}|^{2}=s^{2}+R^{2}.$

Substitution of y = s / R and y = cotφ = cosφ / sinφ, successively, gives

$|{\vec {\mathbf {B} }}|={\frac {ik}{R}}\int _{-\infty }^{\infty }{\frac {dy}{(y^{2}+1)^{3/2}}}={\frac {ik}{R}}\int _{0}^{\pi }\sin \phi \,d\phi ={\frac {2ik}{R}},$

where i is the current and R the distance of the point of observation of the magnetic induction to the wire. The constant k depends on the choice of electromagnetic units and is 10⁻⁷ henry/m [= Vs/A = N/A²] in rationalized SI units. This equation gives the original formulation of Biot and Savart. The SI dimension of B is T [tesla: 1 T = 1 N/(Am), newton divided by ampere meter]. A field of 1 T (SI) corresponds to 10000 gauss (cgs units).

Generalized Biot-Savart-Laplace law

From hereon vectors are indicated by bold letters, arrows on top are omitted.

In the above we wrote i for the current, which is equal to the current density J times the cross section A of the wire. If the current density J is not constant over the cross section, i.e., J = J(r' ), we must use a surface integral over the cross section A. Rather than introducing a surface element, we multiply immediately by ds and obtain an infinitesimal volume element $\scriptstyle d\mathbf {r} '\equiv dV$,

$id\mathbf {s} \rightarrow \iint _{A}\mathbf {J} (\mathbf {r} ')d\mathbf {r} ',$

where we made the current density J into a vector parallel to the segment ds and of magnitude J(r'). The volume element has height ds and base an infinitesimal surface element of the cross section A. The B-field at point r, due to a volume V = As of the current becomes,

$\mathbf {B} (\mathbf {r} )=k\iiint _{V}{\frac {\mathbf {J} (\mathbf {r} ')\times (\mathbf {r} -\mathbf {r'} )}{|\mathbf {r} -\mathbf {r'} |^{3}}}d\mathbf {r} '.$

Note that:

${\frac {\mathbf {r} -\mathbf {r'} }{|\mathbf {r} -\mathbf {r'} |^{3}}}={\boldsymbol {\nabla }}\left({\frac {1}{|\mathbf {r} -\mathbf {r'} |}}\right),$

where we choose the nabla operator to act on the unprimed coordinates and hence it may be moved outside the integral, giving the following generalized form of the Biot-Savart-Laplace law for the magnetic induction at point r:

$\mathbf {B} (\mathbf {r} )=k{\boldsymbol {\nabla }}\times \iiint _{V}{\frac {\mathbf {J} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r'} |}}d\mathbf {r} ',\qquad \qquad \qquad \qquad \qquad \qquad \qquad (1)$

where V is a finite volume of the current generating the B-field. The total B-field is obtained by having V encompass all current (integrating over all current).

Maxwell equations

We will show that the expression for B given in Eq. (1) satisfies the Maxwell equations. This is of interest, since the Maxwell equations can be seen as a set of postulates for classical electrodynamics. We will show that the Biot-Savart-Laplace law is a consequence of the postulates (although Biot and Savart made their discovery some forty-five years before Maxwell formulated his equations).

Since it is known from vector analysis that

${\boldsymbol {\nabla }}\cdot {\Big (}{\boldsymbol {\nabla }}\times \mathbf {V} (\mathbf {r} ){\Big )}=0$

for any vector field V(r), it is immediately clear that B satisfies the following Maxwell equation:

${\boldsymbol {\nabla }}\cdot \mathbf {B} (\mathbf {r} )=0.$

The one other Maxwell equation of interest is

${\boldsymbol {\nabla }}\times \mathbf {B} (\mathbf {r} )=4\pi k\mathbf {J} (\mathbf {r} ),$

where we assumed that there are no time-dependent electric fields present. This equation was first formulated by Ampère, as clearly recognized by Maxwell. In SI units 4πk is equal to the vacuum permeability μ₀. In the proof we will need the following results

${\begin{aligned}{\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times \mathbf {V} )&={\boldsymbol {\nabla }}({\boldsymbol {\nabla }}\cdot \mathbf {V} )-\nabla ^{2}\mathbf {V} \\{\boldsymbol {\nabla }}{\frac {1}{|\mathbf {r} -\mathbf {r'} |}}&=-{\boldsymbol {\nabla }}'{\frac {1}{|\mathbf {r} -\mathbf {r'} |}}\\\nabla ^{2}{\frac {1}{|\mathbf {r} -\mathbf {r'} |}}&=-4\pi \delta (\mathbf {r} -\mathbf {r'} )\\{\boldsymbol {\nabla }}\cdot \mathbf {J} &=0.\\\end{aligned}}$

The first equation is well-known in vector analysis, the second follows by differentiating to the components of r and r' and equating. The third equation has a Dirac delta function on the right-hand side and follows from distribution theory. The last equation follows from charge density (ρ) conservation and the continuity equation,

${\frac {\partial \rho }{\partial t}}=0\quad {\hbox{and}}\quad {\boldsymbol {\nabla }}\cdot \mathbf {J} +{\frac {\partial \rho }{\partial t}}=0,$

respectively. Now:

${\begin{aligned}{\boldsymbol {\nabla }}\times \mathbf {B} &=k{\boldsymbol {\nabla }}\times {\boldsymbol {\nabla }}\times \iiint _{V}{\frac {\mathbf {J} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r'} |}}d\mathbf {r} '\\&=k{\boldsymbol {\nabla }}\iiint \mathbf {J} (\mathbf {r} ')\cdot {\boldsymbol {\nabla }}\left({\frac {1}{|\mathbf {r} -\mathbf {r'} |}}\right)d\mathbf {r} '-k\iiint \mathbf {J} (\mathbf {r} ')\nabla ^{2}\left({\frac {1}{|\mathbf {r} -\mathbf {r'} |}}\right)d\mathbf {r} '\\&=k{\boldsymbol {\nabla }}\iiint {\Big (}{\boldsymbol {\nabla }}'\cdot \mathbf {J} (\mathbf {r} '){\Big )}\left({\frac {1}{|\mathbf {r} -\mathbf {r'} |}}\right)d\mathbf {r} '+4\pi k\iiint \mathbf {J} (\mathbf {r} ')\delta (\mathbf {r} -\mathbf {r'} )d\mathbf {r} '.\\\end{aligned}}$

In the first term of the last step we replaced the unprimed nabla by a primed one (times minus) and then applied a turn-over rule with the primed nabla. This turn-over rule can be justified by partial integration and gives a minus sign, or, in other words, nabla is an anti-hermitian operator. Using that the divergence of the current density vanishes and the defining property of the delta function, we get

${\boldsymbol {\nabla }}\times \mathbf {B} (\mathbf {r} )=4\pi k\mathbf {J} (\mathbf {r} ).$

This shows that B(r) of Eq. (1) (the generalized Biot-Savart-Laplace law) satisfies this Maxwell equation.

References

Further reading:

• J. D. Jackson, Classical Electrodynamics, 2nd edition, John Wiley, New York (1975).