Law of diminishing returns: Difference between revisions
imported>Caesar Schinas m (Bot: Update image code) |
imported>Meg Taylor No edit summary |
||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
The '''law of diminishing returns''' | The '''law of diminishing returns''' is an abstract concept in economic theory. It states that the output per input (productivity) declines if the input of a production factor is increased over a certain limit. It has two versions, one of which is a tautology and the other of which lacks empirical support. | ||
__TOC__ | __TOC__ | ||
==The classical concept== | ==The classical concept== | ||
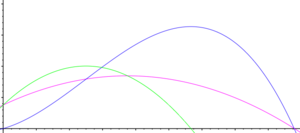
{{Image|Law of diminishing returns.png|right|300px|Production function (blue) with first rising and then diminishing marginal (green) and average (magenta) returns.}} | |||
In [[History of economic thought#Classical_Economics|classical economics]] the | In [[History of economic thought#Classical_Economics|classical economics]] the law states that the highest productivity is gained when there is an optimal proportion between the factors of production. Any divergence from that proportion will result in lower productivity. It is a tautology, being no more than a restatement of the implied definition of the term "optimum". | ||
If one production factor is fixed, the proportion between the production factors will change with rising production i.e. rising input of the variable factor. According to the classical LDR this leads to a production function that has | If one production factor is fixed, the proportion between the production factors will change with rising production i.e. rising input of the variable factor. According to the classical LDR this leads to a production function that has three phases with the following characteristics: | ||
# Rising [[marginal]] productivity, rising average productivity. | # Rising [[marginal]] productivity, rising average productivity. | ||
# Diminishing marginal productivity, rising average productivity. | # Diminishing marginal productivity, rising average productivity. | ||
# Diminishing average productivity. | # Diminishing average productivity. | ||
===History=== | ===History=== | ||
| Line 18: | Line 18: | ||
==The neoclassical concept== | ==The neoclassical concept== | ||
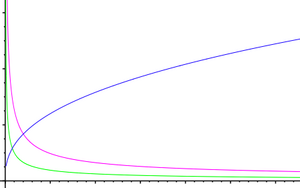
{{Image|Production function with decreasing returns to scale.png|right|300px|Production function (blue) with decreasing returns to scale (green) and therefore decreasing average returns (magenta).}} | {{Image|Production function with decreasing returns to scale.png|right|300px|Production function (blue) with decreasing returns to scale (green) and therefore decreasing average returns (magenta).}} | ||
In [[History of economic thought#Neoclassical_Economics|neoclassical economics]] the | In [[History of economic thought#Neoclassical_Economics|neoclassical economics]] the concept signifies that an increasing input of ''any'' production factor will result in diminishing marginal productivity. This leads to a production function with the following characteristics: | ||
* Zero input of a production factor results in zero output i.e. the graph starts at the [[Origin (Mathematics)|origin]]. | * Zero input of a production factor results in zero output i.e. the graph starts at the [[Origin (Mathematics)|origin]]. | ||
* Marginal productivity is highest with the lowest possible input, i.e. the point closest to an input of zero. | * Marginal productivity is highest with the lowest possible input, i.e. the point closest to an input of zero. | ||
| Line 24: | Line 24: | ||
===History=== | ===History=== | ||
The origins of the neoclassical production function i.e. the neoclassical | The origins of the neoclassical production function i.e. the neoclassical concept date back to the time of classical economics. Then the concept was used to describe the effect of an increase in wheat production where good soils were limited. To increase the production of wheat inferior soils would have to be used, which would deliver less wheat for the same amount of labour.<Ref>David Ricardo, 1772—1823, ''An Essay on Profits'', 1815</ref> | ||
Neoclassical economists extended the idea to the claim that any [[Rationality (Economics)|economically rational]] producer would use any production factor first for the most productive task, then for the next productive task, etc., and/or would use the best unit first, then the second best, etc. Thus the idea got applied to all production factors. | Neoclassical economists extended the idea to the claim that any [[Rationality (Economics)|economically rational]] producer would use any production factor first for the most productive task, then for the next productive task, etc., and/or would use the best unit first, then the second best, etc. Thus the idea got applied to all production factors. | ||
===Implications=== | ===Implications=== | ||
The | The neoclassical concept is a necessary condition for the existence of a stable [[economic equilibrium|equilibrium]] in the abstract theory of [[general equilibrium]], which assumes that the [[production function]] is convex. It has no known "real world" implications. | ||
===Critique=== | ===Critique=== | ||
In the 1920s, the economist Piero Sraffa criticised the concept for its failure to take account of competition among producers and their suppliers<ref>[http://homepage.newschool.edu/~het/texts/sraffa/sraffa26.htm Piero Sraffa: "The Laws of Return Under Competitive Conditions", ''The Economic Journal'' December 1926]</ref>, deeming it to be "so weak as to be unable to support the weight imposed upon (it)", and in the 1960s the eminent economist. Joan Robinsom has described the mathematical statement of the production function as "a powerful instrument of miseducation". | |||
<ref> Joan Robinson: ''Collected Economic Papers'', Blackwell 1960 </ref> | |||
The argumentation on which the neoclassical LDR is based assumes that there are units of a factor with different quality and/or there are fields of application of the factor with different productivity.<Ref>Felderer/Homburg, Makroökonomik und neue Makroökonomik, S. 55, Fn. 4</ref> | The argumentation on which the neoclassical LDR is based assumes that there are units of a factor with different quality and/or there are fields of application of the factor with different productivity.<Ref>Felderer/Homburg, Makroökonomik und neue Makroökonomik, S. 55, Fn. 4</ref> | ||
==Combining both concepts== | ==Combining both concepts== | ||
{{Image|Cobb-Douglas with diminishing returns to scale.png|right|300px|Cobb-Douglas production function with 2 factors and production elasticity complying to the neoclassical LDR, i.e. overall decreasing returns to scale.}} | |||
Neoclassical theory usually distinguishes between only two factors of production: capital and labour. With just two factors of production the production function can be represented by a 3-dimensional graph. | Neoclassical theory usually distinguishes between only two factors of production: capital and labour. With just two factors of production the production function can be represented by a 3-dimensional graph. | ||
| Line 50: | Line 52: | ||
==References== | ==References== | ||
{{reflist}} | |||
Latest revision as of 04:10, 12 October 2013
The law of diminishing returns is an abstract concept in economic theory. It states that the output per input (productivity) declines if the input of a production factor is increased over a certain limit. It has two versions, one of which is a tautology and the other of which lacks empirical support.
The classical concept
In classical economics the law states that the highest productivity is gained when there is an optimal proportion between the factors of production. Any divergence from that proportion will result in lower productivity. It is a tautology, being no more than a restatement of the implied definition of the term "optimum".
If one production factor is fixed, the proportion between the production factors will change with rising production i.e. rising input of the variable factor. According to the classical LDR this leads to a production function that has three phases with the following characteristics:
- Rising marginal productivity, rising average productivity.
- Diminishing marginal productivity, rising average productivity.
- Diminishing average productivity.
History
Historically the concept was first developed by Anne Robert Jacques Turgot. It was mainly related to agricultural production and the use of labour and later fertilizer in relation to a fixed amount of soil.[1]
The neoclassical concept
In neoclassical economics the concept signifies that an increasing input of any production factor will result in diminishing marginal productivity. This leads to a production function with the following characteristics:
- Zero input of a production factor results in zero output i.e. the graph starts at the origin.
- Marginal productivity is highest with the lowest possible input, i.e. the point closest to an input of zero.
- Marginal productivity decreases continuously.
History
The origins of the neoclassical production function i.e. the neoclassical concept date back to the time of classical economics. Then the concept was used to describe the effect of an increase in wheat production where good soils were limited. To increase the production of wheat inferior soils would have to be used, which would deliver less wheat for the same amount of labour.[2]
Neoclassical economists extended the idea to the claim that any economically rational producer would use any production factor first for the most productive task, then for the next productive task, etc., and/or would use the best unit first, then the second best, etc. Thus the idea got applied to all production factors.
Implications
The neoclassical concept is a necessary condition for the existence of a stable equilibrium in the abstract theory of general equilibrium, which assumes that the production function is convex. It has no known "real world" implications.
Critique
In the 1920s, the economist Piero Sraffa criticised the concept for its failure to take account of competition among producers and their suppliers[3], deeming it to be "so weak as to be unable to support the weight imposed upon (it)", and in the 1960s the eminent economist. Joan Robinsom has described the mathematical statement of the production function as "a powerful instrument of miseducation". [4] The argumentation on which the neoclassical LDR is based assumes that there are units of a factor with different quality and/or there are fields of application of the factor with different productivity.[5]
Combining both concepts
Neoclassical theory usually distinguishes between only two factors of production: capital and labour. With just two factors of production the production function can be represented by a 3-dimensional graph.
Tho most prominent production function for creating such a graph is the Cobb-Douglas production function: Y = A × Ca × Lb, where Y stands for yield, C for capital, L for labour, and A, a and b are constants that can be interpreted as A for technology level and a and b for the production elasticities of the factors. This formula can contain elements of both concepts, the classical and the neoclassical LDR.
The classical concept is represented by the fact that a combination of both factors results in a square output so that an even proportion between the factors results in higher productivity.
The neoclassical concept is represented by the fact that each factor has diminishing returns to scale as long as (a < 1) and (b < 1). Note that the combined input of both factors only results in diminishing returns as long as (a + b < 1). If both factors independently have decreasing returns to scale (a < 1, b < 1), their combination might still lead to increasing returns to scale (a + b > 1).
For an interactive demonstration of the Cobb-Douglas production function see: [1]
Naming conventions
Viewing their attributed originators the names for both concepts may seem misleading. Turgot is considered physiocrat, not classical economist, and Ricardo is considered classical, not neoclassical economist. Yet the names of both concepts reflect the eras of their further development and refinement.
References
- ↑ Turgot, Observations sur le mémoire de M. de Saint-Péravy en faveur de l’impôt indirect, 1768. In: Turgot, Anne Robert Jacques (1727—1781), Oeuvres de Turgot, 1966, pp. 418 sqq., (421), Gallica, Bibliothèque nationale de France
- ↑ David Ricardo, 1772—1823, An Essay on Profits, 1815
- ↑ Piero Sraffa: "The Laws of Return Under Competitive Conditions", The Economic Journal December 1926
- ↑ Joan Robinson: Collected Economic Papers, Blackwell 1960
- ↑ Felderer/Homburg, Makroökonomik und neue Makroökonomik, S. 55, Fn. 4