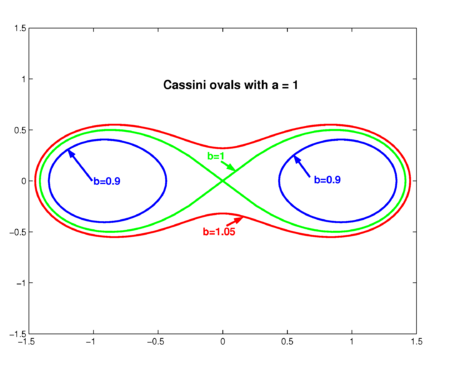
Cassini ovals
A Cassini oval is a locus of points determined by two fixed points F1 and F2 (the "foci") at a distance 2a apart (in the figure the foci are on the x-axis at F1,2 = ±1). If the distance of a certain point to F1 is r1 and the distance of the same point to F2 is r2 then the locus is defined by the product of distances r1×r2 being constant and equal to b2.
The shape of the curves depends on the ratio b : a. If b > a, the curve is a single loop (red curve in the figure)—a dog bone. The case a = b produces a lemniscate of Bernoulli (green curve). The case b < a gives two disconnected ovals (eggs).
The Cassini ovals are a family of quartic curves, also called Cassini ellipses. They are named after Jean-Dominique Cassini (1625–1712) a French-Italian astronomer.