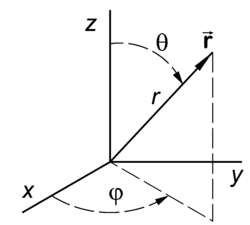
Spherical polar coordinates

Spherical polar coordinates

In mathematics and physics, spherical polar coordinates form a coordinate system for the three-dimensional real space $\scriptstyle \mathbb {R} ^{3}$.

Let x, y, z be Cartesian coordinates of a vector $\scriptstyle {\vec {\mathbf {r} }}$ in $\scriptstyle \mathbb {R} ^{3}$, that is,

${\vec {\mathbf {r} }}=({\vec {\mathbf {e} }}_{x},\,{\vec {\mathbf {e} }}_{y},\,{\vec {\mathbf {e} }}_{z}){\begin{pmatrix}x\\y\\z\\\end{pmatrix}},$

where $\scriptstyle {\vec {\mathbf {e} }}_{x},\,{\vec {\mathbf {e} }}_{y},\,{\vec {\mathbf {e} }}_{z}$ are unit vectors along the x, y, and z axis, respectively. These axes are orthogonal and so are the unit vectors along them.

The length r of the vector $\scriptstyle {\vec {\mathbf {r} }}$ is one of the three numbers necessary to give the position of the vector in three-dimensional space. By applying the theorem of Pythagoras twice it follows that r² = x² + y² + z².

Let θ be the colatitude angle (see the figure) of the vector $\scriptstyle {\vec {\mathbf {r} }}$. In the usual geographic coordinate system used to describe a position on Earth the corresponding latitute angle has its zero at the equator, while the colatitude angle, introduced here, has its zero at the "North Pole", that is, the angle θ is zero when $\scriptstyle {\vec {\mathbf {r} }}$ is along the positive z-axis. The sum of latitude and colatitude angle of a point is 90⁰, which explains the name of the latter.

The angle φ gives the angle with the x-axis of the projection $\scriptstyle {\vec {\mathbf {r} }}'$ of $\scriptstyle {\vec {\mathbf {r} }}$ on the x-y plane. The angle φ is the longitude angle (also known as the azimuthal angle).

Note that the projection $\scriptstyle {\vec {\mathbf {r} }}'$ has length rsinθ. The length of the projection of the latter vector on the x and y axis is therefore rsinθcosφ and rsinθsinφ, respectively. In summary, the spherical polar coordinates r, θ, and φ of $\scriptstyle {\vec {\mathbf {r} }}$ are related to its Cartesian coordinates by

${\begin{aligned}x&=r\sin \theta \cos \phi \\y&=r\sin \theta \sin \phi \\z&=r\cos \theta \end{aligned}}$