Archive:New Draft of the Week

The New Draft of the Week is a chance to highlight a recently created Citizendium article that has just started down the road of becoming a Citizendium masterpiece.
It is chosen each week by vote in a manner similar to that of its sister project, the Article of the Week.

Add New Nominees Here

To add a new nominee or vote for an existing nominee, click edit for this section and follow the instructions Ellesmere Chaucer manuscript Ellipse

Table of Nominees

Nominated article	Vote Score	Supporters	Specialist supporters	Date created
Ellesmere Chaucer manuscript	1	Daniel Mietchen 13:12, 1 May 2010 (UTC)		April 22, 2010

If you want to see how these nominees will look on the CZ home page (if selected as a winner), scroll down a little bit.

Recently created pages are listed on Special:NewPages. A cleaner list is available here.

Transclusion of the above nominees (to be done by an Administrator)

• Transclude each of the nominees in the above "Table of Nominee" as per the instructions at Template:Featured Article Candidate.
• Then add the transcluded article to the list in the next section below, using the {{Featured Article Candidate}} template.

View Current Transcluded Nominees (after they have been transcluded by an Administrator)

The next New Draft of the Week will be the article with the most votes at 1 AM UTC on Thursday, 10 June, 2010.

Nominated article	Supporters	Specialist supporters	Dates	Score
Ellipse: Planar curve formed by the points whose distances to two given points add up to a given number. [e] The metadata subpage is missing. You can start it via filling in this form or by following the instructions that come up after clicking on the [show] link to the right. Do you see this on PREVIEW? then SAVE! before following a link. To find out more about the use of metadata for the management of Citizendium pages, see CZ:Metadata. You may see this box for one of two reasons. Either: A - New page has been created, or subpages template was added to an existing page B - Cluster move is in progress Click either the A or B link for further instructions. [Feel free to recommend improvements to the text or links in this template] A - For a New Cluster use the following directions Subpages format requires a metadata page. Using the following instructions will complete the process of creating this article's subpages. Click the blue "metadata template" link below to create the page. On the edit page that appears paste in the article's title across from "pagename =". You might also fill out the checklist part of the form. Ignore the rest. For background, see Using the Subpages template Don't worry--you'll get the hang of it right away. Remember to hit Save! the "metadata template". However, you can create articles without subpages. Just delete the {{subpages}} template from the top of this page and this prompt will disappear. :) Don't feel obligated to use subpages, it's more important that you write sentences, which you can always do without writing fancy code. [Feel free to recommend improvements to the text or links in this template] B - For a Cluster Move use the following directions The metadata template should be moved to the new name as the first step. Please revert this move and start by using the Move Cluster link at the top left of the talk page. The name prior to this move can be found at the following link. [Feel free to recommend improvements to the text or links in this template] PD Image Fig. 1. Ellipse (black closed curve). The sum of the lengths of the two red line segments (ending in P1) is equal to the sum of the lengths of the two blue line segments (ending in P2). 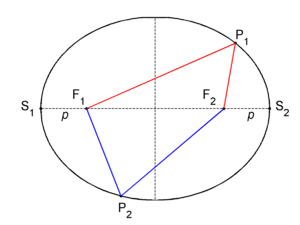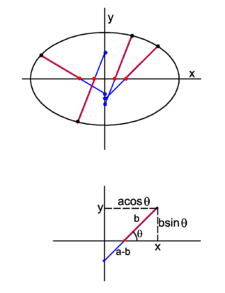In mathematics, an ellipse is a planar locus of points characterized by having a constant sum of distances to two given fixed points in the plane. In figure 1, the two fixed points are F1 and F2, these are the foci of the ellipse. Consider an arbitrary point P1 on the ellipse that has distance F1P1 to F1 and distance F2P1 to F2, and let d be the sum of distances of P1 to the foci, $d:=\mathrm {F} _{1}\mathrm {P} _{1}+\mathrm {F} _{2}\mathrm {P} _{1}\geq \mathrm {F} _{1}\mathrm {F} _{2}\,$ then for all points of the ellipse the sum of distances is also d. Thus, for another arbitrary point P2 on the ellipse with distance F1P2 to F1 and distance F2P2 to F2, by definition, the sum of distances of P2 to the foci is equal to d, $\mathrm {F} _{1}\mathrm {P} _{2}+\mathrm {F} _{2}\mathrm {P} _{2}=d.\,$ The horizontal line segment between S1 and S2 in figure 1, going through the foci, is known as the major axis of the ellipse. Traditionally, the length of the major axis is indicated by 2a. The vertical dashed line segment, drawn halfway between the foci and perpendicular to the major axis, is referred to as the minor axis of the ellipse; its length is usually indicated by 2b. The major and the minor axis are distinguished by a ≥ b. Clearly both ellipse axes are symmetry axes, reflection about either of them transforms the ellipse into itself. Basically, this is a consequence of the fact that reflection preserves (sums of) distances. The intersection of the axes is the center of the ellipse. The two foci and the points S1 and S2 are connected by reflection about the minor axis. Hence the distance S2F2 =: p is, by symmetry, equal to the distance S1F1. The distance of S2 to F1 is equal to 2a − p. By the definition of the ellipse their sum is equal to d, hence $d=(2a-p)+p=2a.\;$ The sum d of distances from any point on the ellipse to the foci is equal to the length of the major axis. Special cases. There are two extreme cases: (a) The first occurs when the two foci coincide. Then a = b and the ellipse is a circle — a special case of an ellipse — and the coinciding foci are the center of the circle. If, in addition, d = 0 then the circle degenerates to a point. (In a circle, any diameter can be chosen as the major axis or as the minor axis.) (b) The second extreme case occurs when the distance of the foci equals d. Then b = 0 and the ellipse degenerates to the line segment bounded by the foci. (Remark: Usually, in common language, these extreme cases are not referred to as an ellipse because "circle" (or "point") and "line segment" describe them better, but in mathematics they are included because they satisfy the definition.) Conic section PD Image Fig. 2. Upper shaded (green) section: ellipse; lower shaded (red) section: circle. 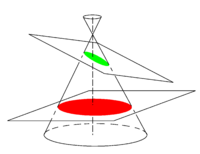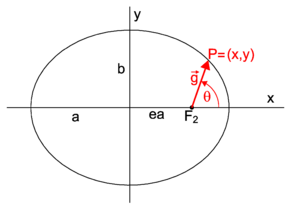In the work of the Greek mathematician Apollonius (c. 262–190 BC) the ellipse arose as the intersection of a plane with a cone. Apollonius gave the ellipse its name, though the term ἔλλειψις (elleipsis, meaning "falling short") was used earlier by Euclid (c. 300 BC) in the construction of parallelograms with areas that "fell short". Apollonius applied the word to the conic section that at present we call ellipse. See Ref. for the—in modern eyes—complicated reasoning by which Apollonius tied the shape of certain conic sections to Euclid's concept of deficient areas. In figure 2 a cone with a circular base is shown. It has a vertical symmetry axis, an axis of revolution. A cone can be generated by revolving around the axis a line that intersects the axis of rotation under an angle α (strictly between 0 and 90 degree). A horizontal plane (plane perpendicular to the axis of the cone) — that does not contain the vertex — intersects the cone in a circle (a special ellipse). A plane that intersects the axis in an angle greater than α intersects the cone in an ellipse. (Otherwise, the intersection is either a parabola or a hyperbola.) If the plane contains the vertex, the ellipse degenerates to a point; if the plane is perpendicular to the axis the ellipse is a circle. Eccentricity The eccentricity e of an ellipse (usually denoted by e or ε) is the ratio of the distance OF2 (cf. figure 3) to the length a (half the major axis), that is, e := OF2 / a. Let ${\vec {a}}$ be a vector of length a along the x-axis, then $e{\vec {a}}:={\overrightarrow {\mathrm {OF} }}_{2}.$ The following two vectors have common endpoint at P, see figure 3, ${\vec {r}}:={\overrightarrow {\mathrm {OP} }}={\begin{pmatrix}x\\y\end{pmatrix}}\quad {\hbox{and}}\quad {\vec {g}}:={\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{2}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=-e{\vec {a}}+{\vec {r}}.$ Now choose P as the intersection P1 of the positive y-axis with the ellipse; then its position vector is: ${\vec {r}}_{1}={\begin{pmatrix}0\\b\end{pmatrix}}.$ By symmetry, the distance of this point P1 to either focus is equal, thus the length of the corresponding vector ${\vec {g}}_{1}$ (with endpoint on the y-axis) is equal to the length a of the semi-major axis. For the following two inner products (indicated by a centered dot) we find, 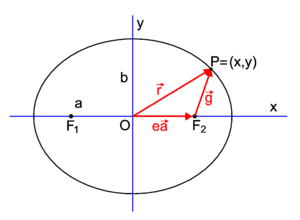${\vec {r}}_{1}\cdot (e{\vec {a}})=0\quad {\hbox{and}}\quad {\vec {r}}_{1}\cdot {\vec {r}}_{1}=b^{2}.$ PD Image Fig. 3. An ellipse situated such that the major and minor axes are along Cartesian axes. The center of the ellipse coincides with the origin O. Hence, (in fact the Pythagoras theorem applied to P1OF2), $a^{2}=|{\vec {g}}_{1}\;|^{2}=({\vec {r}}_{1}-e{\vec {a}}\;)\cdot ({\vec {r}}_{1}-e{\vec {a}}\;)={\vec {r}}_{1}\cdot {\vec {r}}_{1}-2({\vec {r}}_{1}\cdot e{\vec {a}})+e{\vec {a}}\cdot e{\vec {a}}=b^{2}+e^{2}a^{2},$ so that the eccentricity is given by $e={\sqrt {\frac {a^{2}-b^{2}}{a^{2}}}}\quad {\hbox{with}}\quad 0\leq e\leq 1.$ Remark: The two extreme values for the eccentricity correspond to the extreme forms of an ellipse: The vaule 0 corresponds to the circle, the value 1 to the line segment. Algebraic form Consider an ellipse that is located with respect to a Cartesian frame as in figure 3 (a ≥ b > 0, major axis on x-axis, minor axis on y-axis). Then: (Canonical equation of an ellipse) A point P=(x,y) is a point of the ellipse if and only if ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$ Note that for a = b this is the equation of a circle. An ellipse may be seen as a unit circle in which the x and the y coordinates are scaled independently, by 1/a and 1/b, respectively. (An ellipse degenerated to a line segment cannot be described with such an equation.) Proof Part 1: We first consider an arbitrary point P of the ellipse. Introduce the vectors ${\begin{aligned}{\overrightarrow {\mathrm {F} _{1}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{1}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=&\;e{\vec {a}}+{\vec {r}}\\{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{2}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=&-e{\vec {a}}+{\vec {r}}={\vec {g}}\\\end{aligned}}$ By definition of ellipse, the sum of the lengths is 2a $2a=|{\vec {r}}+e{\vec {a}}|+|{\vec {r}}-e{\vec {a}}|\qquad \qquad \qquad \qquad (1)$ Multiplying equation (1) by $|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|$ gives $2a\left(|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|\right)$ $=\left(|{\vec {r}}+e{\vec {a}}|+|{\vec {r}}-e{\vec {a}}|\right)\cdot \left(|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|\right)=|{\vec {r}}+e{\vec {a}}|^{2}-|{\vec {r}}-e{\vec {a}}|^{2}$ $=4e{\vec {r}}\cdot {\vec {a}}$ Hence $|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|={2e{\vec {r}}\cdot {\vec {a}} \over a}$ and since ${\frac {{\vec {r}}\cdot {\vec {a}}}{a}}=x$ (the first coordinate of the vector ${\vec {r}}$) we obtain $|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|=2ex\qquad \qquad \qquad \qquad (2)$ By adding and subtracting equations (1) and (2) we find expressions for the distance of P to the foci, ${\begin{aligned}|{\overrightarrow {\mathrm {F} _{1}\mathrm {P} }}|&=|{\vec {r}}+e{\vec {a}}|&=a+ex&\\|{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}|&=|{\vec {r}}-e{\vec {a}}|&=a-ex&\qquad \qquad \qquad \quad (3)\\\end{aligned}}$ Squaring both equations ${\begin{aligned}r^{2}+e^{2}a^{2}+2e{\vec {r}}\cdot {\vec {a}}&=a^{2}+e^{2}x^{2}+2eax\\r^{2}+e^{2}a^{2}-2e{\vec {r}}\cdot {\vec {a}}&=a^{2}+e^{2}x^{2}-2eax\\\end{aligned}}$ adding them, substituting the earlier derived value for e2, and reworking gives $r^{2}+e^{2}a^{2}=a^{2}+e^{2}x^{2}$ $\Rightarrow r^{2}+{\frac {a^{2}-b^{2}}{a^{2}}}a^{2}=a^{2}+{\frac {a^{2}-b^{2}}{a^{2}}}x^{2}$ $\Rightarrow x^{2}+y^{2}=r^{2}=a^{2}+{\frac {a^{2}-b^{2}}{a^{2}}}(x^{2}-a^{2})=b^{2}+x^{2}-x^{2}{\frac {b^{2}}{a^{2}}}$ $\Rightarrow y^{2}=b^{2}-x^{2}{\frac {b^{2}}{a^{2}}}$ Division by b2 finally gives ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$ Part 2: Conversely, for any point P whose coordinates x and y satisfy this equation, the sum of its distances from the foci $\mathrm {F} _{1}=(-f,0)\quad {\textrm {and}}\quad \mathrm {F} _{2}=(f,0)\quad {\textrm {with}}\quad f:={\sqrt {a^{2}-b^{2}}}$ is $\mathrm {P} \mathrm {F} _{1}+\mathrm {P} \mathrm {F} _{2}=2a$ To show this we calculate $\mathrm {P} \mathrm {F} _{1}^{2}=(x+f)^{2}+y^{2}=x^{2}+y^{2}+f^{2}+2fx$ and substitute for f and $y^{2}=b^{2}-{b^{2} \over a^{2}}x^{2}$ and obtain $\mathrm {P} \mathrm {F} _{1}^{2}=x^{2}+\left(b^{2}-{b^{2} \over a^{2}}x^{2}\right)+(a^{2}-b^{2})+2x{\sqrt {a^{2}-b^{2}}}=a^{2}+2x{\sqrt {a^{2}-b^{2}}}+{a^{2}-b^{2} \over a^{2}}x^{2}=\left(a+{\frac {f}{a}}x\right)^{2}$ After an analogous calculation for F2 we get (note that   $a\pm {\frac {f}{a}}x\geq 0$   because   $-a\leq x\leq a$   and   $0\leq f\leq a$) $\mathrm {P} \mathrm {F} _{1}+\mathrm {P} \mathrm {F} _{2}=(a+{\frac {f}{a}}x)+(a-{\frac {f}{a}}x)=2a$ as claimed. Second degree equation The algebraic form of the previous section describes an ellipse in a special position. Rotation and translation transforms it into an equation of second degree in x and y: $f(x,y):=Ax^{2}+2Bxy+Cy^{2}+2Dx+2Ey+F=0,\,$ (all variables are real). Such an equation always describes a conic section. 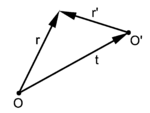It represents a non-degenerate ellipse (minor axis not 0) if and only if the following conditions are satisfied: $AC-B^{2}>0$ $(A+C)f_{t}<0\quad \mathrm {with} \quad f_{t}:=f(t_{1},t_{2})\neq 0$ or, equivalently, $\quad f_{t}>0\Rightarrow A+C<0\quad \mathrm {and} \quad f_{t}<0\Rightarrow A+C>0$ where t1 and t2 are defined as the solutions of the following system of linear equations: ${\begin{matrix}At_{1}+Bt_{2}&=-D\\Bt_{1}+Ct_{2}&=-E\end{matrix}}$ (These equations have a unique solution since, by the first condition, the determinant AC − B2 ≠ 0.) Proof We now switch to matrix-vector notation and write f(x,y) as $f(\mathbf {r} )=\mathbf {r} ^{\mathrm {T} }\mathbf {Q} \mathbf {r} +\mathbf {a} ^{\mathrm {T} }\mathbf {r} +\mathbf {r} ^{\mathrm {T} }\mathbf {a} +F,$ with $\mathbf {r} :={\begin{pmatrix}x\\y\\\end{pmatrix}},\quad \mathbf {Q} :={\begin{pmatrix}A&B\\B&C\\\end{pmatrix}},\quad \mathbf {a} :={\begin{pmatrix}D\\E\\\end{pmatrix}}.$ The superscript T stands for transposition (row vector becomes column vector and vice versa). We first show that the conditions are sufficient: Since, by assumption, the determinant det(Q) = AC−B2 ≠ 0, the matrix Q is invertible. With the help of the inverse Q−1 the equation for f can be rewritten to $f(\mathbf {r} )=\left(\mathbf {r} +\mathbf {Q} ^{-1}\mathbf {a} \right)^{\mathrm {T} }\mathbf {Q} \left(\mathbf {r} +\mathbf {Q} ^{-1}\mathbf {a} \right)-\mathbf {a} ^{\mathrm {T} }\mathbf {Q} ^{-1}\mathbf {a} +F\quad .$ Note that this uses $\mathbf {Q} ^{\mathrm {T} }=\mathbf {Q} \quad \Longrightarrow \quad \left(\mathbf {Q} ^{-1}\right)^{\mathrm {T} }=\mathbf {Q} ^{-1},$ i.e., that both the matrix Q and its inverse are symmetric. PD Image Fig. 4. r′ = r − t Define $\mathbf {t} :=-\mathbf {Q} ^{-1}\mathbf {a} \quad \Longrightarrow \quad \mathbf {Q} \mathbf {t} =-\mathbf {a} ,$ and $\mathbf {r} ':=\mathbf {r} -\mathbf {t} .$ In the definition of t the minus sign is introduced to get the translation of the origin as depicted in figure 4. Now we substitute r′ in the expression for f. (This corresponds to shifting the origin of the coordinate system to the center of the ellipse): $f(\mathbf {r} )=\left(\mathbf {r} -\mathbf {t} \right)^{\mathrm {T} }\mathbf {Q} \left(\mathbf {r} -\mathbf {t} \right)-\mathbf {a} ^{\mathrm {T} }\mathbf {Q} ^{-1}\mathbf {a} +F=\left(\mathbf {r} '\right)^{\mathrm {T} }\mathbf {Q} \mathbf {r} '+f_{t}$ with $f_{t}:=f(\mathbf {t} )=-\mathbf {a} ^{\mathrm {T} }\mathbf {Q} ^{-1}\mathbf {a} +F.$ Thus, by translation of the origin over t   the linear terms in f(r) have been eliminated, only two quadratic terms (in x′ := x−t1 and y′ := y−t2), one bilinear term, and one constant term (ft) appear in the equation for f. (The "price paid" for it is the requirement det(Q) ≠ 0.) In the next step we rotate the coordinate system (around the origin in O') such that the coordinate axes coincide with the axes of the ellipse. This will eliminate the bilinear term and "decouple" x′ and y′, the components of r′. Let us recall that any real symmetric matrix may be diagonalized by an orthogonal matrix. For the (2×2)-case: $\mathbf {R} ^{\mathrm {T} }\mathbf {Q} \mathbf {R} ={\begin{pmatrix}\alpha _{1}&0\\0&\alpha _{2}\end{pmatrix}}\quad {\hbox{with}}\quad \mathbf {R} ^{\mathrm {T} }\mathbf {R} =\mathbf {R} \mathbf {R} ^{\mathrm {T} }=\mathbf {I} ,$ where the last matrix on the right is the identity matrix I. Now $f=\left(\left(\mathbf {r} '\right)^{\mathrm {T} }\;\mathbf {R} \right)\left(\mathbf {R} ^{\mathrm {T} }\;\mathbf {Q} \;\mathbf {R} \right)\left(\mathbf {R} ^{\mathrm {T} }\;\mathbf {r} '\right)+f_{t}=\left(\mathbf {r} ''\right)^{\mathrm {T} }{\boldsymbol {\alpha }}\mathbf {r} ''+f_{t}$ with ${\boldsymbol {\alpha }}:={\begin{pmatrix}\alpha _{1}&0\\0&\alpha _{2}\end{pmatrix}},\quad {\hbox{and}}\quad \mathbf {r} '':=\mathbf {R} ^{\mathrm {T} }\mathbf {r} '.$ Switching back to a quadratic equation $\left(\mathbf {r} ''\right)^{\mathrm {T} }{\boldsymbol {\alpha }}\mathbf {r} ''+f_{t}=\alpha _{1}(x'')^{2}+\alpha _{2}(y'')^{2}+f_{t}=0$ we see that an ellipse is obtained if the parameters α1, α2, and ft are non-zero and if the signs of α1 and α2 are equal and opposite to the sign of ft. It is known that the determinant of a matrix is invariant under similarity transformations, hence $0<\det(\mathbf {Q} )=AC-B^{2}=\alpha _{1}\alpha _{2}$ and the signs of α1 and α2 are equal. The trace A+C of the matrix is also invariant under similarity transformations. Thus $\alpha _{1}+\alpha _{2}=A+C$ and we can apply the assumption ${\begin{aligned}0<\alpha _{1},\alpha _{2}&\quad {\hbox{i.e.}}\quad 0<\alpha _{1}+\alpha _{2}=A+C\quad \Rightarrow \quad f_{t}<0\\0>\alpha _{1},\alpha _{2}&\quad {\hbox{i.e.}}\quad 0>\alpha _{1}+\alpha _{2}=A+C\quad \Rightarrow \quad f_{t}>0\\\end{aligned}}$ and conclude that in both cases the second order equation represents an ellipse. This shows that the conditions given are sufficient. The conditions are also necessary: In the coordinate system determined by its axes, the equation clearly satisfies the conditions, and — since determinant and trace are preserved — they stay satisfied if the system is rotated and shifted. Thus the conditions are necessary if the determinant is not equal to 0. In fact, it is necessary without this assumption on the determinant (see second-order curve). Remark Clearly, in order to determine a priori whether the quadratic equation represents an ellipse, it is not necessary to actually perform the diagonalization of Q. It is sufficient to check the condition and determine the sign of ft = f(t) by solving the equation given for the vector t. Polar representation relative to focus PD Image Fig. 5. Polar representation The length g of a vector (cf. figure 5) from the focus F2 to an endpoint P on the ellipse ${\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}=:{\vec {g}}=(ea+g\cos \theta ,\;g\sin \theta )$ is given by the polar equation of an ellipse (with eccentricity less than 1) $g={\frac {\ell }{1+e\cos \theta }}\quad {\hbox{with}}\quad \ell :={\frac {b^{2}}{a}},$ where 2ℓ is known as the latus rectum (lit. erect side) of the ellipse; it is equal to 2g for θ = 90° (twice the length of the vector ${\vec {g}}$ when it makes a right angle with the major axis). Proof Earlier [Eq. (3)] it was derived for the distance from the right focus F2 to P that $|{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}|=|{\vec {g}}|=g=a-ex.$ Expressing x from $x=ea+g\cos \theta =ea+(a-ex)\cos \theta \,$ gives $x={\frac {ea+a\cos \theta }{1+e\cos \theta }},$ so that $g=a-ex=a-{\frac {e^{2}a+ea\cos \theta }{1+e\cos \theta }}={\frac {a(1-e^{2})}{1+e\cos \theta }}.$ Substitute $a(1-e^{2})=a\left(1-{\frac {a^{2}-b^{2}}{a^{2}}}\right)={\frac {b^{2}}{a}}=\ell$ and the polar equation for the ellipse follows. Trammel construction PD Image Fig. 6. A trammel in theory Before drafting was done almost exclusively by the aid of computers, draftsmen used a simple device for drawing ellipses, a trammel. Basically, a trammel is a rigid bar of length a (semi-major axis). In the top drawing of figure 6 the bar is shown as a blue-red line segment bounded by a black and a blue bead. On this bar a segment of length b (semi-minor axis) is marked; this is the red segment on the bar. Two beads fixed to the rigid bar move back and forth along the x-axis and y-axis, respectively. The blue bead fixed at one end of the bar moves along the y-axis, the red bead, which marks the beginning of the red segment of length b, moves along the x-axis. The endpoint of the bar (the black bead in figure 6) moves along an ellipse with semi-major axis a and semi-minor axis b and typically has a pen fixed to it. (PD)  : http://chestofbooks.com/ Fig. 7. A trammel in practice The fact that the trammel construction works is proved very easily, cf. the bottom drawing in figure 6, $x=a\;\cos \theta \quad {\hbox{and}}\quad y=b\;\sin \theta .$ Hence ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=\cos ^{2}\theta +\sin ^{2}\theta =1,$ which indeed is the equation for an ellipse. A device called a trammel point is used to guide a woodworking router in making elliptical cuts. Gardener's construction (PD)  : http://chestofbooks.com/ Fig. 8. Gardener's construction It is possible to construct an ellipse of given major and minor axes by the aid of a compass, a ruler, three thumbtacks, and a piece of string, see figure 8. First draw the major axis AB, and then obtain with the compass its perpendicular bisector intersecting AB in the midpoint E. Along the bisector one measures off the length of the minor axis CD. Given that the distances CF and CG are the semi-major axis (AB/2), one can determine the foci by drawing an arc with the compass using C as center and AB/2 as radius. One now pins the thumbtacks in the foci and the point C and fixes a piece of string around the triangle FGC (i.e, its length equals the perimeter of the triangle). Removing the thumbtack at C, and keeping the string taut, one draws the ellipse by moving the pencil from C to A, D, B, and back to C. Clearly this procedure can be used in the garden to create an elliptic lawn or flowerbed, which is why the procedure is sometimes referred to as the gardener's construction. Notes Figures 7 and 8 are from George Watson Kittredge, The New Metal Worker Pattern Book, David Williams Company, New York, (1901) Online (Read more...)	Daniel Mietchen 13:12, 1 May 2010 (UTC); Chunbum Park 00:37, 8 May 2010 (UTC)		2

Current Winner

To be selected and implemented by an Administrator. To change, click edit and follow the instructions, or see documentation at {{Featured Article}}.

The metadata subpage is missing. You can start it via filling in this form or by following the instructions that come up after clicking on the [show] link to the right.

Do you see this on PREVIEW? then SAVE! before following a link. To find out more about the use of metadata for the management of Citizendium pages, see CZ:Metadata. You may see this box for one of two reasons. Either: A - New page has been created, or subpages template was added to an existing page B - Cluster move is in progress Click either the A or B link for further instructions. [Feel free to recommend improvements to the text or links in this template] A - For a New Cluster use the following directions Subpages format requires a metadata page. Using the following instructions will complete the process of creating this article's subpages. Click the blue "metadata template" link below to create the page. On the edit page that appears paste in the article's title across from "pagename =". You might also fill out the checklist part of the form. Ignore the rest. For background, see Using the Subpages template Don't worry--you'll get the hang of it right away. Remember to hit Save! the "metadata template". However, you can create articles without subpages. Just delete the {{subpages}} template from the top of this page and this prompt will disappear. :) Don't feel obligated to use subpages, it's more important that you write sentences, which you can always do without writing fancy code. [Feel free to recommend improvements to the text or links in this template] B - For a Cluster Move use the following directions The metadata template should be moved to the new name as the first step. Please revert this move and start by using the Move Cluster link at the top left of the talk page. The name prior to this move can be found at the following link. [Feel free to recommend improvements to the text or links in this template]

---

PD Image
Fig. 1. Ellipse (black closed curve). The sum of the lengths of the two red line segments (ending in P₁) is equal to the sum of the lengths of the two blue line segments (ending in P₂).

In mathematics, an ellipse is a planar locus of points characterized by having a constant sum of distances to two given fixed points in the plane. In figure 1, the two fixed points are F₁ and F₂, these are the foci of the ellipse. Consider an arbitrary point P₁ on the ellipse that has distance F₁P₁ to F₁ and distance F₂P₁ to F₂, and let d be the sum of distances of P₁ to the foci,

$d:=\mathrm {F} _{1}\mathrm {P} _{1}+\mathrm {F} _{2}\mathrm {P} _{1}\geq \mathrm {F} _{1}\mathrm {F} _{2}\,$

then for all points of the ellipse the sum of distances is also d. Thus, for another arbitrary point P₂ on the ellipse with distance F₁P₂ to F₁ and distance F₂P₂ to F₂, by definition, the sum of distances of P₂ to the foci is equal to d,

$\mathrm {F} _{1}\mathrm {P} _{2}+\mathrm {F} _{2}\mathrm {P} _{2}=d.\,$

The horizontal line segment between S₁ and S₂ in figure 1, going through the foci, is known as the major axis of the ellipse. Traditionally, the length of the major axis is indicated by 2a. The vertical dashed line segment, drawn halfway between the foci and perpendicular to the major axis, is referred to as the minor axis of the ellipse; its length is usually indicated by 2b. The major and the minor axis are distinguished by a ≥ b.

Clearly both ellipse axes are symmetry axes, reflection about either of them transforms the ellipse into itself. Basically, this is a consequence of the fact that reflection preserves (sums of) distances. The intersection of the axes is the center of the ellipse.

The two foci and the points S₁ and S₂ are connected by reflection about the minor axis. Hence the distance S₂F₂ =: p is, by symmetry, equal to the distance S₁F₁. The distance of S₂ to F₁ is equal to 2a − p. By the definition of the ellipse their sum is equal to d, hence

$d=(2a-p)+p=2a.\;$

The sum d of distances from any point on the ellipse to the foci is equal to the length of the major axis.

Special cases. There are two extreme cases:
(a) The first occurs when the two foci coincide. Then a = b and the ellipse is a circle — a special case of an ellipse — and the coinciding foci are the center of the circle. If, in addition, d = 0 then the circle degenerates to a point. (In a circle, any diameter can be chosen as the major axis or as the minor axis.)
(b) The second extreme case occurs when the distance of the foci equals d. Then b = 0 and the ellipse degenerates to the line segment bounded by the foci.
(Remark: Usually, in common language, these extreme cases are not referred to as an ellipse because "circle" (or "point") and "line segment" describe them better, but in mathematics they are included because they satisfy the definition.)

Conic section

PD Image
Fig. 2. Upper shaded (green) section: ellipse; lower shaded (red) section: circle.

In the work of the Greek mathematician Apollonius (c. 262–190 BC) the ellipse arose as the intersection of a plane with a cone. Apollonius gave the ellipse its name, though the term ἔλλειψις (elleipsis, meaning "falling short") was used earlier by Euclid (c. 300 BC) in the construction of parallelograms with areas that "fell short". Apollonius applied the word to the conic section that at present we call ellipse. See Ref. for the—in modern eyes—complicated reasoning by which Apollonius tied the shape of certain conic sections to Euclid's concept of deficient areas.

In figure 2 a cone with a circular base is shown. It has a vertical symmetry axis, an axis of revolution. A cone can be generated by revolving around the axis a line that intersects the axis of rotation under an angle α (strictly between 0 and 90 degree). A horizontal plane (plane perpendicular to the axis of the cone) — that does not contain the vertex — intersects the cone in a circle (a special ellipse). A plane that intersects the axis in an angle greater than α intersects the cone in an ellipse. (Otherwise, the intersection is either a parabola or a hyperbola.) If the plane contains the vertex, the ellipse degenerates to a point; if the plane is perpendicular to the axis the ellipse is a circle.

Eccentricity

The eccentricity e of an ellipse (usually denoted by e or ε) is the ratio of the distance OF₂ (cf. figure 3) to the length a (half the major axis), that is, e := OF₂ / a. Let ${\vec {a}}$ be a vector of length a along the x-axis, then

$e{\vec {a}}:={\overrightarrow {\mathrm {OF} }}_{2}.$

The following two vectors have common endpoint at P, see figure 3,

${\vec {r}}:={\overrightarrow {\mathrm {OP} }}={\begin{pmatrix}x\\y\end{pmatrix}}\quad {\hbox{and}}\quad {\vec {g}}:={\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{2}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=-e{\vec {a}}+{\vec {r}}.$

Now choose P as the intersection P₁ of the positive y-axis with the ellipse; then its position vector is:

${\vec {r}}_{1}={\begin{pmatrix}0\\b\end{pmatrix}}.$

By symmetry, the distance of this point P₁ to either focus is equal, thus the length of the corresponding vector ${\vec {g}}_{1}$ (with endpoint on the y-axis) is equal to the length a of the semi-major axis. For the following two inner products (indicated by a centered dot) we find,

${\vec {r}}_{1}\cdot (e{\vec {a}})=0\quad {\hbox{and}}\quad {\vec {r}}_{1}\cdot {\vec {r}}_{1}=b^{2}.$

PD Image
Fig. 3. An ellipse situated such that the major and minor axes are along Cartesian axes. The center of the ellipse coincides with the origin O.

Hence, (in fact the Pythagoras theorem applied to P₁OF₂),

$a^{2}=|{\vec {g}}_{1}\;|^{2}=({\vec {r}}_{1}-e{\vec {a}}\;)\cdot ({\vec {r}}_{1}-e{\vec {a}}\;)={\vec {r}}_{1}\cdot {\vec {r}}_{1}-2({\vec {r}}_{1}\cdot e{\vec {a}})+e{\vec {a}}\cdot e{\vec {a}}=b^{2}+e^{2}a^{2},$

so that the eccentricity is given by

$e={\sqrt {\frac {a^{2}-b^{2}}{a^{2}}}}\quad {\hbox{with}}\quad 0\leq e\leq 1.$

Remark: The two extreme values for the eccentricity correspond to the extreme forms of an ellipse: The vaule 0 corresponds to the circle, the value 1 to the line segment.

Algebraic form

Consider an ellipse that is located with respect to a Cartesian frame as in figure 3 (a ≥ b > 0, major axis on x-axis, minor axis on y-axis). Then:

(Canonical equation of an ellipse) A point P=(x,y) is a point of the ellipse if and only if

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$

Note that for a = b this is the equation of a circle. An ellipse may be seen as a unit circle in which the x and the y coordinates are scaled independently, by 1/a and 1/b, respectively. (An ellipse degenerated to a line segment cannot be described with such an equation.)

Proof

Part 1: We first consider an arbitrary point P of the ellipse. Introduce the vectors

${\begin{aligned}{\overrightarrow {\mathrm {F} _{1}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{1}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=&\;e{\vec {a}}+{\vec {r}}\\{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{2}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=&-e{\vec {a}}+{\vec {r}}={\vec {g}}\\\end{aligned}}$

By definition of ellipse, the sum of the lengths is 2a

$2a=|{\vec {r}}+e{\vec {a}}|+|{\vec {r}}-e{\vec {a}}|\qquad \qquad \qquad \qquad (1)$

Multiplying equation (1) by

$|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|$

gives

$2a\left(|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|\right)$

$=\left(|{\vec {r}}+e{\vec {a}}|+|{\vec {r}}-e{\vec {a}}|\right)\cdot \left(|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|\right)=|{\vec {r}}+e{\vec {a}}|^{2}-|{\vec {r}}-e{\vec {a}}|^{2}$

$=4e{\vec {r}}\cdot {\vec {a}}$

Hence

$|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|={2e{\vec {r}}\cdot {\vec {a}} \over a}$

and since

${\frac {{\vec {r}}\cdot {\vec {a}}}{a}}=x$

(the first coordinate of the vector ${\vec {r}}$) we obtain

$|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|=2ex\qquad \qquad \qquad \qquad (2)$

By adding and subtracting equations (1) and (2) we find expressions for the distance of P to the foci,

${\begin{aligned}|{\overrightarrow {\mathrm {F} _{1}\mathrm {P} }}|&=|{\vec {r}}+e{\vec {a}}|&=a+ex&\\|{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}|&=|{\vec {r}}-e{\vec {a}}|&=a-ex&\qquad \qquad \qquad \quad (3)\\\end{aligned}}$

Squaring both equations

${\begin{aligned}r^{2}+e^{2}a^{2}+2e{\vec {r}}\cdot {\vec {a}}&=a^{2}+e^{2}x^{2}+2eax\\r^{2}+e^{2}a^{2}-2e{\vec {r}}\cdot {\vec {a}}&=a^{2}+e^{2}x^{2}-2eax\\\end{aligned}}$

adding them, substituting the earlier derived value for e², and reworking gives

$r^{2}+e^{2}a^{2}=a^{2}+e^{2}x^{2}$

$\Rightarrow r^{2}+{\frac {a^{2}-b^{2}}{a^{2}}}a^{2}=a^{2}+{\frac {a^{2}-b^{2}}{a^{2}}}x^{2}$

$\Rightarrow x^{2}+y^{2}=r^{2}=a^{2}+{\frac {a^{2}-b^{2}}{a^{2}}}(x^{2}-a^{2})=b^{2}+x^{2}-x^{2}{\frac {b^{2}}{a^{2}}}$

$\Rightarrow y^{2}=b^{2}-x^{2}{\frac {b^{2}}{a^{2}}}$

Division by b² finally gives

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$

Part 2: Conversely, for any point P whose coordinates x and y satisfy this equation, the sum of its distances from the foci

$\mathrm {F} _{1}=(-f,0)\quad {\textrm {and}}\quad \mathrm {F} _{2}=(f,0)\quad {\textrm {with}}\quad f:={\sqrt {a^{2}-b^{2}}}$

is

$\mathrm {P} \mathrm {F} _{1}+\mathrm {P} \mathrm {F} _{2}=2a$

To show this we calculate

$\mathrm {P} \mathrm {F} _{1}^{2}=(x+f)^{2}+y^{2}=x^{2}+y^{2}+f^{2}+2fx$

and substitute for f and

$y^{2}=b^{2}-{b^{2} \over a^{2}}x^{2}$

and obtain

$\mathrm {P} \mathrm {F} _{1}^{2}=x^{2}+\left(b^{2}-{b^{2} \over a^{2}}x^{2}\right)+(a^{2}-b^{2})+2x{\sqrt {a^{2}-b^{2}}}=a^{2}+2x{\sqrt {a^{2}-b^{2}}}+{a^{2}-b^{2} \over a^{2}}x^{2}=\left(a+{\frac {f}{a}}x\right)^{2}$

After an analogous calculation for F₂ we get (note that   $a\pm {\frac {f}{a}}x\geq 0$   because   $-a\leq x\leq a$   and   $0\leq f\leq a$)

$\mathrm {P} \mathrm {F} _{1}+\mathrm {P} \mathrm {F} _{2}=(a+{\frac {f}{a}}x)+(a-{\frac {f}{a}}x)=2a$

as claimed.

Second degree equation

The algebraic form of the previous section describes an ellipse in a special position. Rotation and translation transforms it into an equation of second degree in x and y:

$f(x,y):=Ax^{2}+2Bxy+Cy^{2}+2Dx+2Ey+F=0,\,$

(all variables are real). Such an equation always describes a conic section.

It represents a non-degenerate ellipse (minor axis not 0) if and only if the following conditions are satisfied:

• $AC-B^{2}>0$

• $(A+C)f_{t}<0\quad \mathrm {with} \quad f_{t}:=f(t_{1},t_{2})\neq 0$

or, equivalently, $\quad f_{t}>0\Rightarrow A+C<0\quad \mathrm {and} \quad f_{t}<0\Rightarrow A+C>0$

where t₁ and t₂ are defined as the solutions of the following system of linear equations:

${\begin{matrix}At_{1}+Bt_{2}&=-D\\Bt_{1}+Ct_{2}&=-E\end{matrix}}$

(These equations have a unique solution since, by the first condition, the determinant AC − B² ≠ 0.)

Proof

We now switch to matrix-vector notation and write f(x,y) as

$f(\mathbf {r} )=\mathbf {r} ^{\mathrm {T} }\mathbf {Q} \mathbf {r} +\mathbf {a} ^{\mathrm {T} }\mathbf {r} +\mathbf {r} ^{\mathrm {T} }\mathbf {a} +F,$

with

$\mathbf {r} :={\begin{pmatrix}x\\y\\\end{pmatrix}},\quad \mathbf {Q} :={\begin{pmatrix}A&B\\B&C\\\end{pmatrix}},\quad \mathbf {a} :={\begin{pmatrix}D\\E\\\end{pmatrix}}.$

The superscript T stands for transposition (row vector becomes column vector and vice versa).

We first show that the conditions are sufficient:

Since, by assumption, the determinant det(Q) = AC−B² ≠ 0, the matrix Q is invertible. With the help of the inverse Q⁻¹ the equation for f can be rewritten to

$f(\mathbf {r} )=\left(\mathbf {r} +\mathbf {Q} ^{-1}\mathbf {a} \right)^{\mathrm {T} }\mathbf {Q} \left(\mathbf {r} +\mathbf {Q} ^{-1}\mathbf {a} \right)-\mathbf {a} ^{\mathrm {T} }\mathbf {Q} ^{-1}\mathbf {a} +F\quad .$

Note that this uses

$\mathbf {Q} ^{\mathrm {T} }=\mathbf {Q} \quad \Longrightarrow \quad \left(\mathbf {Q} ^{-1}\right)^{\mathrm {T} }=\mathbf {Q} ^{-1},$

i.e., that both the matrix Q and its inverse are symmetric.

PD Image
Fig. 4. r′ = r − t

Define

$\mathbf {t} :=-\mathbf {Q} ^{-1}\mathbf {a} \quad \Longrightarrow \quad \mathbf {Q} \mathbf {t} =-\mathbf {a} ,$

and

$\mathbf {r} ':=\mathbf {r} -\mathbf {t} .$

In the definition of t the minus sign is introduced to get the translation of the origin as depicted in figure 4.

Now we substitute r′ in the expression for f. (This corresponds to shifting the origin of the coordinate system to the center of the ellipse):

$f(\mathbf {r} )=\left(\mathbf {r} -\mathbf {t} \right)^{\mathrm {T} }\mathbf {Q} \left(\mathbf {r} -\mathbf {t} \right)-\mathbf {a} ^{\mathrm {T} }\mathbf {Q} ^{-1}\mathbf {a} +F=\left(\mathbf {r} '\right)^{\mathrm {T} }\mathbf {Q} \mathbf {r} '+f_{t}$

with

$f_{t}:=f(\mathbf {t} )=-\mathbf {a} ^{\mathrm {T} }\mathbf {Q} ^{-1}\mathbf {a} +F.$

Thus, by translation of the origin over t   the linear terms in f(r) have been eliminated, only two quadratic terms (in x′ := x−t₁ and y′ := y−t₂), one bilinear term, and one constant term (f_t) appear in the equation for f. (The "price paid" for it is the requirement det(Q) ≠ 0.)

In the next step we rotate the coordinate system (around the origin in O') such that the coordinate axes coincide with the axes of the ellipse. This will eliminate the bilinear term and "decouple" x′ and y′, the components of r′.

Let us recall that any real symmetric matrix may be diagonalized by an orthogonal matrix. For the (2×2)-case:

$\mathbf {R} ^{\mathrm {T} }\mathbf {Q} \mathbf {R} ={\begin{pmatrix}\alpha _{1}&0\\0&\alpha _{2}\end{pmatrix}}\quad {\hbox{with}}\quad \mathbf {R} ^{\mathrm {T} }\mathbf {R} =\mathbf {R} \mathbf {R} ^{\mathrm {T} }=\mathbf {I} ,$

where the last matrix on the right is the identity matrix I. Now

$f=\left(\left(\mathbf {r} '\right)^{\mathrm {T} }\;\mathbf {R} \right)\left(\mathbf {R} ^{\mathrm {T} }\;\mathbf {Q} \;\mathbf {R} \right)\left(\mathbf {R} ^{\mathrm {T} }\;\mathbf {r} '\right)+f_{t}=\left(\mathbf {r} ''\right)^{\mathrm {T} }{\boldsymbol {\alpha }}\mathbf {r} ''+f_{t}$

with

${\boldsymbol {\alpha }}:={\begin{pmatrix}\alpha _{1}&0\\0&\alpha _{2}\end{pmatrix}},\quad {\hbox{and}}\quad \mathbf {r} '':=\mathbf {R} ^{\mathrm {T} }\mathbf {r} '.$

Switching back to a quadratic equation

$\left(\mathbf {r} ''\right)^{\mathrm {T} }{\boldsymbol {\alpha }}\mathbf {r} ''+f_{t}=\alpha _{1}(x'')^{2}+\alpha _{2}(y'')^{2}+f_{t}=0$

we see that an ellipse is obtained if the parameters α₁, α₂, and f_t are non-zero and if the signs of α₁ and α₂ are equal and opposite to the sign of f_t.

It is known that the determinant of a matrix is invariant under similarity transformations, hence

$0<\det(\mathbf {Q} )=AC-B^{2}=\alpha _{1}\alpha _{2}$

and the signs of α₁ and α₂ are equal.

The trace A+C of the matrix is also invariant under similarity transformations. Thus

$\alpha _{1}+\alpha _{2}=A+C$

and we can apply the assumption

${\begin{aligned}0<\alpha _{1},\alpha _{2}&\quad {\hbox{i.e.}}\quad 0<\alpha _{1}+\alpha _{2}=A+C\quad \Rightarrow \quad f_{t}<0\\0>\alpha _{1},\alpha _{2}&\quad {\hbox{i.e.}}\quad 0>\alpha _{1}+\alpha _{2}=A+C\quad \Rightarrow \quad f_{t}>0\\\end{aligned}}$

and conclude that in both cases the second order equation represents an ellipse. This shows that the conditions given are sufficient.

The conditions are also necessary:

In the coordinate system determined by its axes, the equation clearly satisfies the conditions, and — since determinant and trace are preserved — they stay satisfied if the system is rotated and shifted. Thus the conditions are necessary if the determinant is not equal to 0. In fact, it is necessary without this assumption on the determinant (see second-order curve).

Remark
Clearly, in order to determine a priori whether the quadratic equation represents an ellipse, it is not necessary to actually perform the diagonalization of Q. It is sufficient to check the condition and determine the sign of f_t = f(t) by solving the equation given for the vector t.

Polar representation relative to focus

PD Image
Fig. 5. Polar representation

The length g of a vector (cf. figure 5) from the focus F₂ to an endpoint P on the ellipse

${\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}=:{\vec {g}}=(ea+g\cos \theta ,\;g\sin \theta )$

is given by the polar equation of an ellipse (with eccentricity less than 1)

$g={\frac {\ell }{1+e\cos \theta }}\quad {\hbox{with}}\quad \ell :={\frac {b^{2}}{a}},$

where 2ℓ is known as the latus rectum (lit. erect side) of the ellipse; it is equal to 2g for θ = 90^° (twice the length of the vector ${\vec {g}}$ when it makes a right angle with the major axis).

Proof

Earlier [Eq. (3)] it was derived for the distance from the right focus F₂ to P that

$|{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}|=|{\vec {g}}|=g=a-ex.$

Expressing x from

$x=ea+g\cos \theta =ea+(a-ex)\cos \theta \,$

gives

$x={\frac {ea+a\cos \theta }{1+e\cos \theta }},$

so that

$g=a-ex=a-{\frac {e^{2}a+ea\cos \theta }{1+e\cos \theta }}={\frac {a(1-e^{2})}{1+e\cos \theta }}.$

Substitute

$a(1-e^{2})=a\left(1-{\frac {a^{2}-b^{2}}{a^{2}}}\right)={\frac {b^{2}}{a}}=\ell$

and the polar equation for the ellipse follows.

Trammel construction

PD Image
Fig. 6. A trammel in theory

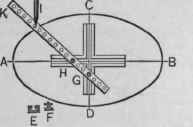
Before drafting was done almost exclusively by the aid of computers, draftsmen used a simple device for drawing ellipses, a trammel. Basically, a trammel is a rigid bar of length a (semi-major axis). In the top drawing of figure 6 the bar is shown as a blue-red line segment bounded by a black and a blue bead. On this bar a segment of length b (semi-minor axis) is marked; this is the red segment on the bar. Two beads fixed to the rigid bar move back and forth along the x-axis and y-axis, respectively. The blue bead fixed at one end of the bar moves along the y-axis, the red bead, which marks the beginning of the red segment of length b, moves along the x-axis. The endpoint of the bar (the black bead in figure 6) moves along an ellipse with semi-major axis a and semi-minor axis b and typically has a pen fixed to it.

(PD)  : http://chestofbooks.com/
Fig. 7. A trammel in practice

The fact that the trammel construction works is proved very easily, cf. the bottom drawing in figure 6,

$x=a\;\cos \theta \quad {\hbox{and}}\quad y=b\;\sin \theta .$

Hence

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=\cos ^{2}\theta +\sin ^{2}\theta =1,$

which indeed is the equation for an ellipse.

A device called a trammel point is used to guide a woodworking router in making elliptical cuts.

Gardener's construction

(PD)  : http://chestofbooks.com/
Fig. 8. Gardener's construction

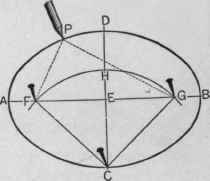
It is possible to construct an ellipse of given major and minor axes by the aid of a compass, a ruler, three thumbtacks, and a piece of string, see figure 8.

First draw the major axis AB, and then obtain with the compass its perpendicular bisector intersecting AB in the midpoint E. Along the bisector one measures off the length of the minor axis CD. Given that the distances CF and CG are the semi-major axis (AB/2), one can determine the foci by drawing an arc with the compass using C as center and AB/2 as radius. One now pins the thumbtacks in the foci and the point C and fixes a piece of string around the triangle FGC (i.e, its length equals the perimeter of the triangle). Removing the thumbtack at C, and keeping the string taut, one draws the ellipse by moving the pencil from C to A, D, B, and back to C.

Clearly this procedure can be used in the garden to create an elliptic lawn or flowerbed, which is why the procedure is sometimes referred to as the gardener's construction.

Notes

Figures 7 and 8 are from George Watson Kittredge, The New Metal Worker Pattern Book, David Williams Company, New York, (1901) Online (Read more...)

Previous Winners

•  Aeneid [r]: An epic poem written by Virgil, which depicts the hero Aeneas fleeing from Troy (ancient city), journeying to Carthage, Sicily, and finally to Italy where after battling, he becomes the precursor of the city of Rome; a monumental work of major significance in Western literature. ^[e]
•  Tall tale [r]: A narrative, song or jest, transmitted orally or in writing, presenting an incredible, boastful or impossible story. ^[e]
•  Plane (geometry) [r]: In elementary geometry, a flat surface that entirely contains all straight lines passing through two of its points. ^[e]
•  Steam [r]: The vapor (or gaseous) phase of water (H₂O). ^[e]
•  Wasan [r]: Classical Japanese mathematics that flourished during the Edo Period from the 17th to mid-19th centuries. ^[e]
•  Racism in Australia [r]: The history of racism and restrictive immigration policies in the Commonwealth of Australia. ^[e]
• Think tank [r]: Add brief definition or description
•  Les Paul [r]: (9 June 1915 – 13 August 2009) American innovator, inventor, musician and songwriter, who was notably a pioneer in the development of the solid-body electric guitar. ^[e]
•  Zionism [r]: The ideology that Jews should form a Jewish state in what is traced as the Biblical area of Palestine; there are many interpretations, including the boundaries of such a state and its criteria for citizenship ^[e] (September 3)
•  Earth's atmosphere [r]: An envelope of gas that surrounds the Earth and extends from the Earth's surface out thousands of kilometres, becoming increasingly thinner (less dense) with distance but always held in place by Earth's gravitational pull. ^[e] (August 27)
•  Joshua Lawrence Chamberlain [r]: U.S. educator deeply bonded to Bowdoin College, from undergraduate to President; American Civil War general and recipient of the Medal of Honor; Governor of Maine ^[e] (August 20)
•  The Sporting Life (album) [r]: A 1994 studio album recorded by Diamanda Galás and John Paul Jones. ^[e] (August 13}
•  The Rolling Stones [r]: Famous and influential English blues rock group formed in 1962, known for their albums Let It Bleed and Sticky Fingers, and songs '(I Can't Get No) Satisfaction' and 'Start Me Up'. ^[e] (August 5)
•  Euler angles [r]: three rotation angles that describe any rotation of a 3-dimensional object. ^[e] (July 30)
•  Chester Nimitz [r]: United States Navy admiral (1885-1966) who was Commander in Chief, Pacific and Pacific Ocean Areas in World War II ^[e] (July 23)
•  Heat [r]: A form of energy that flows spontaneously from hotter to colder bodies that are in thermal contact. ^[e] (July 16)
•  Continuum hypothesis [r]: A statement about the size of the continuum, i.e., the number of elements in the set of real numbers. ^[e] (July 9)
•  Hawaiian alphabet [r]: The form of writing used in the Hawaiian Language ^[e] (July 2)
•  Now and Zen [r]: A 1988 studio album recorded by Robert Plant, with guest contributions from Jimmy Page. ^[e] (June 25)
•  Wrench (tool) [r]: A fastening tool used to tighten or loosen threaded fasteners, with one end that makes firm contact with flat surfaces of the fastener, and the other end providing a means of applying force ^[e] (June 18)
•  Air preheater [r]: A general term to describe any device designed to preheat the combustion air used in a fuel-burning furnace for the purpose of increasing the thermal efficiency of the furnace. ^[e] (June 11)
•  2009 H1N1 influenza virus [r]: A contagious influenza A virus discovered in April 2009, commonly known as swine flu. ^[e] (June 4)
•  Gasoline [r]: A fuel for spark-ignited internal combustion engines derived from petroleum crude oil. ^[e] (21 May)
•  John Brock [r]: Fictional British secret agent who starred in three 1960s thrillers by Desmond Skirrow. ^[e] (8 May)
•  McGuffey Readers [r]: A set of highly influential school textbooks used in the 19th and early 20th centuries in the elementary grades in the United States. ^[e] (14 Apr)
•  Vector rotation [r]: Process of rotating one unit vector into a second unit vector. ^[e] (7 Apr)
•  Leptin [r]: Hormone secreted by adipocytes that regulates appetite. ^[e] (31 Mar)
•  Kansas v. Crane [r]: Add brief definition or description (24 Mar)
•  Punch card [r]: Add brief definition or description (17 Mar)
•  Jass–Belote card games [r]: Add brief definition or description (10 Mar)
•  Leptotes (orchid) [r]: Add brief definition or description (3 Mar)
•  Worm (computers) [r]: Add brief definition or description (24 Feb)
•  Joseph Black [r]: Add brief definition or description (11 Feb 2009)
•  Sympathetic magic [r]: Add brief definition or description (17 Jan 2009)
•  Dien Bien Phu [r]: Add brief definition or description (25 Dec)
• Blade Runner [r]: Add brief definition or description (25 Nov)
•  Piquet [r]: Add brief definition or description (18 Nov)
•  Crash of 2008 [r]: Add brief definition or description (23 Oct)
• Information Management [r]: Add brief definition or description (31 Aug)
•  Battle of Gettysburg [r]: Add brief definition or description (8 July)
•  Drugs banned from the Olympics [r]: Add brief definition or description (1 July)
•  Sea glass [r]: Add brief definition or description (24 June)
•  Dazed and Confused (Led Zeppelin song) [r]: Add brief definition or description (17 June)
•  Hirohito [r]: Add brief definition or description (10 June)
•  Henry Kissinger [r]: Add brief definition or description (3 June)
• Palatalization [r]: Add brief definition or description (27 May)
•  Intelligence on the Korean War [r]: Add brief definition or description (20 May)
•  Trinity United Church of Christ, Chicago [r]: Add brief definition or description (13 May)
•  BIOS [r]: Add brief definition or description (6 May)
•  Miniature Fox Terrier [r]: Add brief definition or description (23 April)
•  Joseph II [r]: Add brief definition or description (15 Apr)
•  British and American English [r]: Add brief definition or description (7 Apr)
•  Count Rumford [r]: Add brief definition or description (1 April)
•  Whale meat [r]: Add brief definition or description (25 March)
•  Naval guns [r]: Add brief definition or description (18 March)
•  Sri Lanka [r]: Add brief definition or description (11 March)
•  Led Zeppelin [r]: Add brief definition or description (4 March)
•  Martin Luther [r]: Add brief definition or description (20 February)
•  Cosmology [r]: Add brief definition or description (4 February)
•  Ernest Rutherford [r]: Add brief definition or description(28 January)
•  Edinburgh [r]: Add brief definition or description (21 January)
•  Russian Revolution of 1905 [r]: Add brief definition or description (8 January 2008)
•  Phosphorus [r]: Add brief definition or description (31 December)
•  John Tyler [r]: Add brief definition or description (6 December)
•  Banana [r]: Add brief definition or description (22 November)
•  Augustin-Louis Cauchy [r]: Add brief definition or description (15 November)
• B-17 Flying Fortress (bomber) [r]: Add brief definition or description - 8 November 2007
•  Red Sea Urchin [r]: Add brief definition or description - 1 November 2007
•  Symphony [r]: Add brief definition or description - 25 October 2007
•  Oxygen [r]: Add brief definition or description - 18 October 2007
•  Origins and architecture of the Taj Mahal [r]: Add brief definition or description - 11 October 2007
•  Fossilization (palaeontology) [r]: Add brief definition or description - 4 October 2007
•  Cradle of Humankind [r]: Add brief definition or description - 27 September 2007
•  John Adams [r]: Add brief definition or description - 20 September 2007
•  Quakers [r]: Add brief definition or description - 13 September 2007
•  Scarborough Castle [r]: Add brief definition or description - 6 September 2007
•  Jane Addams [r]: Add brief definition or description - 30 August 2007
•  Epidemiology [r]: Add brief definition or description - 23 August 2007
•  Gay community [r]: Add brief definition or description - 16 August 2007
•  Edward I [r]: Add brief definition or description - 9 August 2007

Rules and Procedure

Rules

• The primary criterion of eligibility for a new draft is that it must have been ranked as a status 1 or 2 (developed or developing), as documented in the History of the article's Metadate template, no more than one month before the date of the next selection (currently every Thursday).
• Any Citizen may nominate a draft.
• No Citizen may have nominated more than one article listed under "current nominees" at a time.
• The article's nominator is indicated simply by the first name in the list of votes (see below).
• At least for now--while the project is still small--you may nominate and vote for drafts of which you are a main author.
• An article can be the New Draft of the Week only once. Nominated articles that have won this honor should be removed from the list and added to the list of previous winners.
• Comments on nominations should be made on the article's talk page.
• Any draft will be deleted when it is past its "last date eligible". Don't worry if this happens to your article; consider nominating it as the Article of the Week.
• If an editor believes that a nominee in his or her area of expertise is ineligible (perhaps due to obvious and embarrassing problems) he or she may remove the draft from consideration. The editor must indicate the reasons why he has done so on the nominated article's talk page.

Nomination

See above section "Add New Nominees Here".

Voting

• To vote, add your name and date in the Supporters column next to an article title, after other supporters for that article, by signing <br />~~~~. (The date is necessary so that we can determine when the last vote was added.) Your vote is alloted a score of 1.
• Add your name in the Specialist supporters column only if you are an editor who is an expert about the topic in question. Your vote is alloted a score of 1 for articles that you created and 2 for articles that you did not create.
• You may vote for as many articles as you wish, and each vote counts separately, but you can only nominate one at a time; see above. You could, theoretically, vote for every nominated article on the page, but this would be pointless.

Ranking

• The list of articles is sorted by number of votes first, then alphabetically.
• Admins should make sure that the votes are correctly tallied, but anyone may do this. Note that "Specialist Votes" are worth 3 points.

Updating

• Each Thursday, one of the admins listed below should move the winning article to the Current Winner section of this page, announce the winner on Citizendium-L and update the "previous winning drafts" section accordingly.
• The winning article will be the article at the top of the list (ie the one with the most votes).
• In the event of two or more having the same number of votes :
  • The article with the most specialist supporters is used. Should this fail to produce a winner, the article appearing first by English alphabetical order is used.
    
  • The remaining winning articles are guaranteed this position in the following weeks, again in alphabetical order. No further voting should take place on these, which remain at the top of the table with notices to that effect. Further nominations and voting take place to determine future winning articles for the following weeks.
  • Winning articles may be named New Draft of the Week beyond their last eligible date if their circumstances are so described above.

Administrators

The Administrators of this program are the same as the admins for CZ:Article of the Week.

See Also

• CZ:Article of the Week
• CZ:Markup tags for partial transclusion of selected text in an article
• CZ:Monthly Write-a-Thon

|width=10% align=center style="background:#F5F5F5"|  |}