User:John R. Brews/WP Import

(PD) Image: John R. Brews
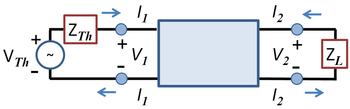
Two-port network with symbol definitions. A Thevenin voltage source with Thevenin impedance Z_Th drives port 1, and impedance Z_L loads port 2

A Two Port Network (or four-terminal network, or quadrapole) is an electrical circuit or device with two pairs of terminals. As shown in the figure, two terminals constitute a port only if they satisfy the essential requirement known as the port condition, namely, the same current must enter and leave a port. Examples include small-signal models for transistors (such as the hybrid-pi model), filters and matching networks. The analysis of passive two-port networks is an outgrowth of reciprocity theorems first derived by Lorentz.

A two-port network makes possible the replacement of either a complete circuit or part of it by a "black box" with a set of distinctive properties, enabling us to abstract its behavior from its internal realization, thus simplifying analysis. Any linear circuit with four terminals can be transformed into a two-port network provided that it does not contain an independent source and satisfies the port conditions.

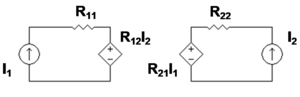
The parameters used in order to describe a two-port network are the following: z, y, h, g, T. They are usually expressed in matrix notation and they establish relations between the following parameters (see Figure 1):

${V_{1}}$ = Input voltage

${V_{2}}$ = Output voltage

${I_{1}}$ = Input current

${I_{2}}$ = Output current

These variables are most useful at low to moderate frequencies. At high frequencies (for example, microwave frequencies) power and energy are more useful variables, and the two-port approach based on current and voltages that is discussed here is replaced by an approach based upon scattering parameters.

Though some authors use the terms two-port network and four-terminal network interchangeably, the latter represents a more general concept. Not all four-terminal networks are two-port networks. A pair of terminals can be called a port only if the current entering one is equal to the current leaving the other (the port condition). Only those four-terminal networks in which the four terminals can be paired into two ports can be called two-ports.

Impedance parameters (z-parameters)

Figure 2: z-equivalent two port showing independent variables I₁ and I₂. Although resistors are shown, general impedances can be used instead.

$\left[{\begin{array}{c}V_{1}\\V_{2}\end{array}}\right]=\left[{\begin{array}{cc}z_{11}&z_{12}\\z_{21}&z_{22}\end{array}}\right]\left[{\begin{array}{c}I_{1}\\I_{2}\end{array}}\right]$.

$z_{11}={V_{1} \over I_{1}}{\bigg |}_{I_{2}=0}\qquad z_{12}={V_{1} \over I_{2}}{\bigg |}_{I_{1}=0}$

$z_{21}={V_{2} \over I_{1}}{\bigg |}_{I_{2}=0}\qquad z_{22}={V_{2} \over I_{2}}{\bigg |}_{I_{1}=0}$

Notice that all the z-parameters have dimensions of ohms.

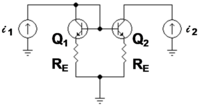
Example: bipolar current mirror with emitter degeneration

Figure 3: Bipolar current mirror: i₁ is the reference current and i₂ is the output current; lower case symbols indicate these are total currents that include the DC components

Figure 4: Small-signal bipolar current mirror: I₁ is the amplitude of the small-signal reference current and I₂ is the amplitude of the small-signal output current

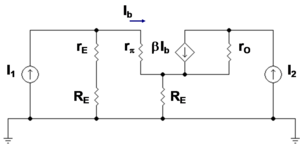
Figure 3 shows a bipolar current mirror with emitter resistors to increase its output resistance. Transistor Q₁ is diode connected, which is to say its collector-base voltage is zero. Figure 4 shows the small-signal circuit equivalent to Figure 3. Transistor Q₁ is represented by its emitter resistance r_E ≈ V_T / I_E (V_T = thermal voltage, I_E = Q-point emitter current), a simplification made possible because the dependent current source in the hybrid-pi model for Q₁ draws the same current as a resistor 1 / g_m connected across r_π. The second transistor Q₂ is represented by its hybrid-pi model. Table 1 below shows the z-parameter expressions that make the z-equivalent circuit of Figure 2 electrically equivalent to the small-signal circuit of Figure 4.

Table 1	Expression	Approximation
$R_{21}={\begin{matrix}{V_{\mathrm {2} } \over I_{\mathrm {1} }}\end{matrix}}{\Big |}_{I_{2}=0}$	$-(\beta r_{O}-R_{E})$ ${\begin{matrix}{\frac {r_{E}+R_{E}}{r_{\pi }+r_{E}+2R_{E}}}\end{matrix}}$	$-\beta r_{o}$${\begin{matrix}{\frac {r_{E}+R_{E}}{r_{\pi }+2R_{E}}}\end{matrix}}$
$R_{11}={\begin{matrix}{\frac {V_{1}}{I_{1}}}\end{matrix}}{\Big |}_{I_{2}=0}$	$(r_{E}+R_{E})$ $//$ $(r_{\pi }+R_{E})$	${\displaystyle }$
$R_{22}={\begin{matrix}{\frac {V_{2}}{I_{2}}}\end{matrix}}{\Big |}_{I_{1}=0}$	$\ ($$1+\beta$ ${\begin{matrix}{\frac {R_{E}}{r_{\pi }+r_{E}+2R_{E}}}\end{matrix}})$ $r_{O}$ $+{\begin{matrix}{\frac {r_{\pi }+r_{E}+R_{E}}{r_{\pi }+r_{E}+2R_{E}}}\end{matrix}}$$R_{E}$	$\ ($$1+\beta$${\begin{matrix}{\frac {R_{E}}{r_{\pi }+2R_{E}}}\end{matrix}})$ $r_{O}$
$R_{12}={\begin{matrix}{V_{\mathrm {1} } \over I_{\mathrm {2} }}\end{matrix}}{\Big |}_{I_{1}=0}$	$R_{E}$ ${\begin{matrix}{\frac {r_{E}+R_{E}}{r_{\pi }+r_{E}+2R_{E}}}\end{matrix}}$	$R_{E}$ ${\begin{matrix}{\frac {r_{E}+R_{E}}{r_{\pi }+2R_{E}}}\end{matrix}}$

The negative feedback introduced by resistors R_E can be seen in these parameters. For example, when used as an active load in a differential amplifier, I₁ ≈ -I₂, making the output impedance of the mirror approximately R₂₂ -R₂₁ ≈ 2 β r_OR_E /( r_π+2R_E ) compared to only r_O without feedback (that is with R_E = 0 Ω) . At the same time, the impedance on the reference side of the mirror is approximately R₁₁ -R₁₂ ≈ Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} \frac {r_{\pi}} {r_{\pi}+2R_E} \end{matrix} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (r_E+R_E)} , only a moderate value, but still larger than r_E with no feedback. In the differential amplifier application, a large output resistance increases the difference-mode gain, a good thing, and a small mirror input resistance is desirable to avoid Miller effect.

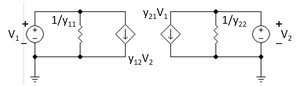
Admittance parameters (y-parameters)

Figure 5: Y-equivalent two port showing independent variables V₁ and V₂. Although resistors are shown, general admittances can be used instead.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \begin{array}{c} I_1 \\ I_2 \end{array} \right] = \left[ \begin{array}{cc} y_{11} & y_{12} \\ y_{21} & y_{22} \end{array} \right] \left[ \begin{array}{c}V_1 \\ V_2 \end{array} \right] } .

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{11} = {I_1 \over V_1 } \bigg|_{V_2 = 0} \qquad y_{12} = {I_1 \over V_2 } \bigg|_{V_1 = 0}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{21} = {I_2 \over V_1 } \bigg|_{V_2 = 0} \qquad y_{22} = {I_2 \over V_2 } \bigg|_{V_1 = 0}}

The network is said to be reciprocal if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{12} = y_{21}} . Notice that all the Y-parameters have dimensions of siemens.

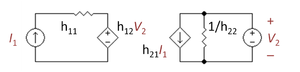
Hybrid parameters (h-parameters)

Figure 6: H-equivalent two-port showing independent variables I₁ and V₂; h₂₂ is reciprocated to make a resistor

${V_{1} \choose I_{2}}={\begin{pmatrix}h_{11}&h_{12}\\h_{21}&h_{22}\end{pmatrix}}{I_{1} \choose V_{2}}$.

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{11} = {V_1 \over I_1 } \bigg|_{V_2 = 0} \qquad h_{12} = {V_1 \over V_2 } \bigg|_{I_1 = 0}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{21} = {I_2 \over I_1 } \bigg|_{V_2 = 0} \qquad h_{22} = {I_2 \over V_2 } \bigg|_{I_1 = 0}}

Often this circuit is selected when a current amplifier is wanted at the output. The resistors shown in the diagram can be general impedances instead.

Notice that off-diagonal h-parameters are dimensionless, while diagonal members have dimensions the reciprocal of one another.

Example: common base amplifier

Figure 7: Common-base amplifier with AC current source I₁ as signal input and unspecified load supporting voltage V₂ and a dependent current I₂.

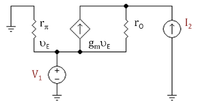
Note: Tabulated formulas in Table 2 make the h-equivalent circuit of the transistor from Figure 6 agree with its small-signal low-frequency hybrid-pi model in Figure 7. Notation: r_π = base resistance of transistor, r_O = output resistance, and g_m = transconductance. The negative sign for h₂₁ reflects the convention that I₁, I₂ are positive when directed into the two-port. A non-zero value for h₁₂ means the output voltage affects the input voltage, that is, this amplifier is bilateral. If h₁₂ = 0, the amplifier is unilateral.

Table 2	Expression	Approximation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{21} = \begin{matrix} {I_\mathrm{2} \over I_\mathrm{1} }\end{matrix} \Big|_{V_{2}=0} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} - \frac {\frac {\beta }{\beta+1}r_O +r_E} {r_O+r_E} \end{matrix} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} - \frac {\beta }{\beta+1}\end{matrix} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{11}= \begin{matrix} \frac{V_{1}}{I_{1}}\end{matrix} \Big|_{V_{2}=0} }	$r_{E}//r_{O}$	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_E}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{22} = \begin{matrix} \frac{I_{2}}{V_{2}}\end{matrix} \Big|_{I_{1}=0} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} \frac {1} {( \beta +1) ( r_O +r_E)} \end{matrix} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} \frac {1} {( \beta +1) r_O } \end{matrix} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{12} = \begin{matrix} {V_\mathrm{1} \over V_\mathrm{2} }\end{matrix} \Big|_{I_{1}=0} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \begin{matrix} \frac {r_E} {r_E+r_O} \end{matrix} \ }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \begin{matrix} \frac {r_E} {r_O} \end{matrix} \ } << 1

Inverse hybrid parameters (g-parameters)

Figure 8: G-equivalent two-port showing independent variables V₁ and I₂; g₁₁ is reciprocated to make a resistor

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {I_1 \choose V_2} = \begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22} \end{pmatrix}{V_1 \choose I_2} } .

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{11} = {I_1 \over V_1 } \bigg|_{I_2 = 0} \qquad g_{12} = {I_1 \over I_2 } \bigg|_{V_1 = 0}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{21} = {V_2 \over V_1 } \bigg|_{I_2 = 0} \qquad g_{22} = {V_2 \over I_2 } \bigg|_{V_1 = 0}}

Often this circuit is selected when a voltage amplifier is wanted at the output. Notice that off-diagonal g-parameters are dimensionless, while diagonal members have dimensions the reciprocal of one another. The resistors shown in the diagram can be general impedances instead.

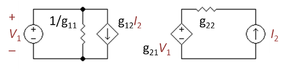
Example: common base amplifier

Figure 9: Common-base amplifier with AC voltage source V₁ as signal input and unspecified load delivering current I₂ at a dependent voltage V₂.

Note: Tabulated formulas in Table 3 make the g-equivalent circuit of the transistor from Figure 8 agree with its small-signal low-frequency hybrid-pi model in Figure 9. Notation: r_π = base resistance of transistor, r_O = output resistance, and g_m = transconductance. The negative sign for g₁₂ reflects the convention that I₁, I₂ are positive when directed into the two-port. A non-zero value for g₁₂ means the output current affects the input current, that is, this amplifier is bilateral. If g₁₂ = 0, the amplifier is unilateral.

Table 3	Expression
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{21} = \begin{matrix} {V_\mathrm{2} \over V_\mathrm{1} }\end{matrix} \Big|_{I_{2}=0} }	$g_{m}r_{O}+1$
$g_{11}={\begin{matrix}{\frac {I_{1}}{V_{1}}}\end{matrix}}{\Big |}_{I_{2}=0}$	${\begin{matrix}{\frac {1}{r_{\pi }}}\end{matrix}}$
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{22} = \begin{matrix} \frac{V_{2}}{I_{2}} \Big|_{V_{1}=0} \end{matrix}}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_O }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{12} = \begin{matrix} {I_\mathrm{1} \over I_\mathrm{2} }\end{matrix} \Big|_{V_{1}=0} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 }

ABCD-parameters

The ABCD-parameters are known variously as chain, cascade, or transmission parameters.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {V_1 \choose I_1} = \begin{pmatrix} A & B \\ C & D \end{pmatrix}{V_2 \choose I_2} } .

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = {V_1 \over V_2 } \bigg|_{I_2 = 0} \qquad B = {V_1 \over I_2 } \bigg|_{V_2 = 0}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = {I_1 \over V_2 } \bigg|_{I_2 = 0} \qquad D = {I_1 \over I_2 } \bigg|_{V_2 = 0}}

Note that we have inserted negative signs in front of the fractions in the definitions of parameters B and D. The reason for adpoting this convention (as opposed to the convention adopted above for the other sets of parameters) is that it allows us to represent the transmission matrix of cascades of two or more two-port networks as simple matrix multiplications of the matrices of the individual networks. This convention is equivalent to reversing the direction of I₂ so that it points in the same direction as the input current to the next stage in the cascaded network.

This technique is exactly analogous to the use of ABCD matrices for ray tracing in the science of optics. See also ray transfer matrix.

Table of transmission parameters

The table below lists transmission parameters for some simple network elements.

Element	Matrix	Remarks
Series resistor	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 & -R \\ 0 & 1 \end{pmatrix} }	R = resistance
Shunt resistor	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 & 0 \\ -1/R & 1 \end{pmatrix} }	R = resistance
Series conductor	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 & -1/G \\ 0 & 1 \end{pmatrix} }	G = conductance
Shunt conductor	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 & 0 \\ -G & 1 \end{pmatrix} }	G = conductance
Series inductor	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 & -Ls \\ 0 & 1 \end{pmatrix} }	L = inductance s = complex angular frequency
Shunt capacitor	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} 1 & 0 \\ -Cs & 1 \end{pmatrix} }	C = capacitance s = complex angular frequency

Combinations of two-port networks

Series connection of two 2-port networks: Z = Z1 + Z2
Parallel connection of two 2-port networks: Y = Y1 + Y2

Example: Cascading two networks

Suppose we have a two-port network consisting of a series resistor R followed by a shunt capacitor C. We can model the entire network as a cascade of two simpler networks:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{T}_1 = \begin{pmatrix} 1 & -R \\ 0 & 1 \end{pmatrix} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{T}_2 = \begin{pmatrix} 1 & 0 \\ -Cs & 1 \end{pmatrix} }

The transmission matrix for the entire network T is simply the matrix multiplication of the transmission matrices for the two network elements:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{T} = \mathbf{T}_2 \cdot \mathbf{T}_1 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \begin{pmatrix} 1 & 0 \\ -Cs & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -R \\ 0 & 1 \end{pmatrix}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \begin{pmatrix} 1 & -R \\ -Cs & 1+RCs \end{pmatrix} }

Thus:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} V_2 \\ I_2 \end{pmatrix} = \begin{pmatrix} 1 & -R \\ -Cs & 1+RCs \end{pmatrix} \begin{pmatrix} V_1 \\ I_1 \end{pmatrix}}

Notes regarding definition of transmission parameters

1) It should be noted that all these examples are specific to the definition of transmission parameters given here. Other definitions exist in the literature, such as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {V_1 \choose I_1} = \begin{pmatrix} A & B \\ C & D \end{pmatrix}{V_2 \choose -I_2} }

2) The format used above for cascading (ABCD) examples cause the "components" to be used backwards compared to standard electronics schematic conventions. This can be fixed by taking the transpose of the above formulas, or by making the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_1, I_1 } the left hand side (dependent variables). Another advantage of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_1, I_1 } form is that the output can be terminated (via a transfer matrix representation of the load) and then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2 } can be set to zero; allowing the voltage transfer function, 1/A to be read directly.

3) In all cases the ABCD matrix terms and current definitions should allow cascading. 4

Networks with more than 2 ports

While two port networks are very common (e.g. amplifiers and filters), other electrical networks such as directional couplers and isolators have more than 2 ports. The following representations can be extended to networks with an arbitrary number of ports:

• Admittance (Y) Parameters
• Impedance (Z) Parameters
• Scattering (S) Parameters

They are extended by adding appropriate terms to the matrix representing the other ports. So 3 port impedance parameters result in the following relationship:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \begin{array}{c} V_1 \\ V_2 \\V_3 \end{array} \right] = \left[ \begin{array}{ccc} Z_{11} & Z_{12} & Z_{13} \\ Z_{21} & Z_{22} &Z_{23} \\ Z_{31} & Z_{32} & Z_{33} \end{array} \right] \left[ \begin{array}{c}I_1 \\ I_2 \\I_3 \end{array} \right] } .

It should be noted that the following representations cannot be extended to more than two ports:

• Hybrid (h) parameters
• Inverse hybrid (g) parameters
• Transmission (ABCD) parameters
• Scattering Transmission (T) parameters