Chemical bond

In chemistry, a chemical bond is a force that keeps atoms together. Certain pairs of atoms can form a stable chemically bonded entity (a diatomic molecule), examples being two nitrogen atoms chemically bound to the stable molecule N—N (written as N₂) and a hydrogen atom with a fluorine atom forming hydrogen fluoride (HF). It can also happen that two bound atoms are part of a larger aggregate. For instance, carbon (C) and oxygen (O) form the pair C—O in the molecule methanol H₃C—OH. The C—O pair, which is strongly bound and easily recognizable, appears in many organic molecules. Atoms may also be bound to form a crystal, such as sodium (Na) and chlorine (Cl) that appear in a 1-1 ratio in crystalline rock (kitchen) salt (NaCl). A diamond crystal can be seen as one huge molecule consisting of bonded C—C (carbon-carbon) pairs.

If the total energy of two or more atoms is lower than the sum of the energies of the component atoms, the atoms bind together to form a molecule (or crystal) and the energy lowering is the binding energy of the molecule (or crystal).

Traditionally one distinguishes the following types of bonds:

• Covalent bonds (also known as homopolar bonds). A single covalent bond between two atoms is due to an electron pair shared by the atoms. These bonds are very common in organic chemistry. They occur between, for instance, hydrogen, carbon, nitrogen, and oxygen atoms and give rise to stable, recognizable, molecules. Most covalently bonded molecules remain intact in the solid, liquid, and gaseous aggregation states. Covalent bonding requires quantum mechanics for an explanation and deeper understanding.
• Ionic bonds. Here one atom, say A, loses an electron to its bonding partner, call it B. Hence A becomes the cation A⁺ and B the anion B⁻. Consecutively, the pair A⁺B⁻ binds strongly through Coulomb interaction. Systems of which the atoms are bound by ionic interactions are usually crystals, the example of rock salt (Na⁺—Cl⁻) was already mentioned. It requires advanced laboratory techniques to separate ionically bound molecules from crystals, as the crystals are usually very stable. Ionically bound compounds usually dissolve easily in water, dissociating into cations and anions.
• Metallic bonds. A number of metal atoms can crystallize to form a metal, which is a solid recognized by high electric and thermal conductivity. The bonding is caused by delocalized electrons forming electronic bands. The mechanism is akin to the formation of molecular orbitals in molecules. An explanation of metallic bonding is offered by quantum mechanics. Metal molecules (M₂, M₃, etc.) are not easily prepared experimentally because solid metals are usually very stable.
• Intermolecular (also known as Van der Waals) bonds. These are bonds between stable molecules, see the articles intermolecular forces and Van der Waals forces for more details. Bonds between stable molecules are usually a few orders of magnitude (factors 100 to 10 000) weaker than covalent and ionic bonds. For many years it was believed that hydrogen bonding was to be classified as a separate type of bond, but modern theoretical chemistry recognizes it as a special type of a (fairly strong) intermolecular bond.

It took several centuries before chemical bonding was fully understood, but at present it is generally accepted that non-relativistic quantum mechanical explanations based on Coulomb's electrostatic law give satisfactory accounts of all kinds of bonds. Gravitational forces, strong nuclear forces, or even magnetic forces, do not play any significant role in chemical bonding.

Octet rule

The octet rule is a simple rule that describes the valency of light atoms (atomic number Z ≤ 18, first and second row of the periodic system). The valency of an atom is the number of covalent bonds that the atom can make with a partner. The octet rule starts with the assumption that valency involves only the electrons in the outer shells of the (lowest-energy-state) atoms participating in the bonding. The following lists the number of valence electrons of the first 18 chemical elements

H(1)	He(2)
Li(1)	Be(2)	B(3)	C(4)	N(5)	O(6)	F(7)	Ne(8)
Na(1)	Mg(2)	Al(3)	Si(4)	P(5)	S(6)	Cl(7)	Ar(8)

The assumption is that the electron configurations of noble gases (He, Ne, Ar) are particularly stable (since these gases are chemically inert) and that a bonded atom strives toward the configuration of the noble gas at the end of its row in the periodic table. Except for hydrogen, which strives for for a helium configuration of two electrons (a duplet), it means that an atom tries to surround himself with an octet of eight electrons. Of course electrons must be shared with bonding partners to achieve a noble gas configuration.

PD Image
Examples of octet rule.

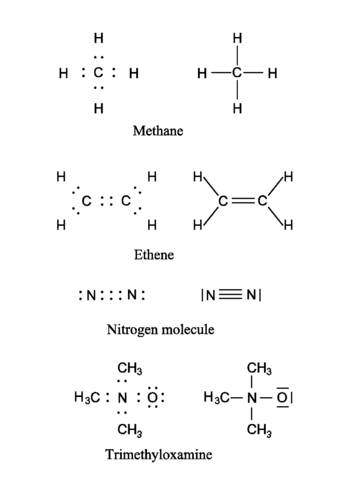
In the figure four molecules are shown as examples. Both the Lewis representation (electrons as dots) and the corresponding traditional chemical representation (chemical bonds as lines) are shown. In the first molecule (methane, CH₄) the hydrogen atoms have a helium electronic configuration (are surrounded by two electrons) and the carbon has a neon configuration (is surrounded by an octet consisting of eight electrons). In the computation of the formal charge on the atoms it is assumed that the electrons in a bond are shared equally by the bonding partners. Thus, in methane the hydrogen atoms have one electron, while the carbon atom has four. From the above table it follows that the hydrogens and the carbon are formally electrically neutral in CH₄. The ethene (formerly known as ethylene) molecule shows a double bond between the carbon atoms. Note that both carbons have a neon configuration (are surrounded by four electron pairs). The next molecule (the nitrogen molecule N₂) shows a triple bond. Both N-atoms are surrounded by an octet (four electron pairs). Each N-atom has five electrons and is formally neutral. The last molecule (trimethyloxamine) has as central atom a nitrogen atom with four electrons, and hence the nitrogen lacks an electron and has a formal charge +1. The oxygen atom has three pairs to itself and shares one pair, carrying seven electrons, so that oxygen has the formal charge −1. The total trimethyloxamine molecule is neutral.

Historical note

The octet rule is usually attributed to Gilbert Newton Lewis, who referred to it as the "rule of eight". The term "octet rule" is due to Irving Langmuir, who extended and refined the work of Lewis. Lewis saw an atom as a cube with—depending on the atom—one to eight valence electrons on its corners. In this picture molecules consist of cubes piled on top of each other, or next to each other sharing a side or a corner. In Ref. it is argued that this idea is not as novel as it is usually believed, but that the idea of eight valences was floating among contemporary chemists and that, for instance, the German chemist Richard Abegg presented already in 1902 some bonding concepts that came close to Lewis's 1916 ideas. In any case, it is generally accepted that Lewis was the first to see the importance of electron pairing. Lewis made the simple assumption that all atomic "kernels" (nuclei plus inner shell electrons) repel one another, and that molecules are held together only by the pairs of electrons which are held jointly by the component atoms.

It is remarkable how far physics and chemistry still were separated during the first two decades of the twentieth century. Neither Lewis nor Langmuir put much faith in the Rutherford-Bohr planetary model of the atom in which the negative electrons orbit a positive nucleus. Both chemists believed electrons to be stationary on the vertices of cubic atoms. On the other hand, the founding fathers of quantum mechanical bonding theory (the physicists Walter Heitler, Fritz London, Georg Rumer, Edward Teller, and others) completely ignored the chemists (or perhaps were not even aware of their work). Linus Pauling deserves the credit for having bridged the two branches of science, which he did in a series of papers in the early 1930s and in his famous 1939 book The Nature of the Chemical Bond that is dedicated to G. N. Lewis. In modern chemistry textbooks, chemical bonding theory is usually presented as a continuous development from Lewis's concepts to the Heitler-London theory for the binding in H₂. Such a presentation of the development in the ideas of chemical binding is a historic oversimplification.

Heitler-London theory

See also molecular orbitals for a treatment of the binding in H₂.

PD Image
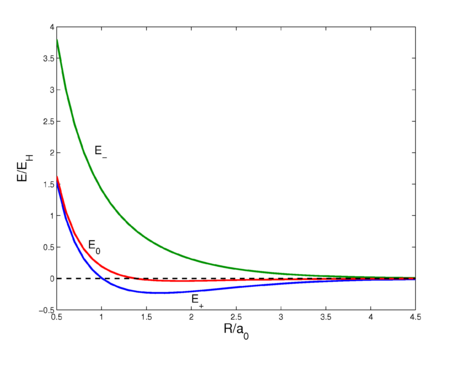
Fig. 2. Interaction energy curves as a function of the H—H distance in H₂. The energy E₀ is of the unsymmetrized wave function, E₊ is of the symmetric wave function, and E₋ is the energy of the antisymmetric wave function. See this page for the code that prepared this plot.

The first satisfactory explanation of the covalent (homopolar) binding in a diatomic molecule was given by Heitler and London in 1927, who used (the then new) quantum mechanics. They considered the simplest neutral diatomic: the hydrogen molecule. They showed that chemical bonding in this two-electron system was obtained when the indistinguishability of the electrons was accounted for.

The basic idea of Heitler and London was to use the product of the wave functions of the separate hydrogen atoms as an approximation of the molecular wave function. The hydrogen atom wave functions are

$\phi _{a}(1)\equiv {\sqrt {\frac {1}{a_{0}^{3}\pi }}}\;e^{-r_{1\mathrm {A} }/a_{0}}\quad {\hbox{and}}\quad \phi _{b}(2)\equiv {\sqrt {\frac {1}{a_{0}^{3}\pi }}}\;e^{-r_{2\mathrm {B} }/a_{0}}$

where r_1A is the distance of electron 1 to hydrogen nucleus A. Likewise r_2B is the distance of electron 2 to nucleus B. The quantity a₀ is the Bohr radius (= 52.9 pm). The functions are normalized to unity,

$\int \phi _{a}(1)^{2}\;\mathrm {d} x_{1\mathrm {A} }\mathrm {d} y_{1\mathrm {A} }\mathrm {d} z_{1\mathrm {A} }=\int \phi _{b}(2)^{2}\;\mathrm {d} x_{2\mathrm {B} }\mathrm {d} y_{2\mathrm {B} }\mathrm {d} z_{2\mathrm {B} }=1$

where the integrals are over all of ℝ³. The product function is an eigenfunction of the sum of two hydrogen-atom Hamiltonians,

$H^{(0)}\phi _{a}(1)\phi _{b}(2)\equiv \left[{\Big (}-{\frac {\hbar ^{2}}{2m_{e}}}\nabla _{1}^{2}-{\frac {1}{r_{1\mathrm {A} }}}{\Big )}+{\Big (}-{\frac {\hbar ^{2}}{2m_{e}}}\nabla _{2}^{2}-{\frac {1}{r_{2\mathrm {B} }}}{\Big )}\right]\phi _{a}(1)\phi _{b}(2)=-2E_{\mathrm {H} }\phi _{a}(1)\phi _{b}(2),$

where the electron-nucleus Coulomb interactions are expressed in Gaussian units. Unit of charge is such that electrons have charge −1 and the hydrogen nuclei +1. The quantity ∇² is the nabla operator squared (acting on the coordinates of electron 1 and 2, respectively); ℏ is Planck's constant and m_e is the mass of an electron. The quantity E_H is the energy of one free hydrogen atom in its ground state (≈ 13.6 electronvolt).

The Heitler-London approach is basically first-order perturbation theory, with H⁽⁰⁾ as unperturbed operator and an interaction (perturbation) operator V that consists of Coulomb terms only

$V=-{\frac {1}{r_{1\mathrm {B} }}}-{\frac {1}{r_{2\mathrm {A} }}}+{\frac {1}{r_{12}}}+{\frac {1}{R_{\mathrm {AB} }}}.$

Here R_AB is the distance between the nuclei and r₁₂ is the distance between the electrons. If one interprets φ_a(1)² as the charge distribution of electron 1 and φ_b(2)² of electron 2, the classical electrostatic energy between the two (non-polarizable) charge distributions is

$E_{0}(R)\equiv \int \int \phi _{a}(1)^{2}\;V\;\phi _{b}(2)^{2}\;\mathrm {d} x_{1\mathrm {A} }\mathrm {d} y_{1\mathrm {A} }\mathrm {d} z_{1\mathrm {A} }\mathrm {d} x_{2\mathrm {B} }\mathrm {d} y_{2\mathrm {B} }\mathrm {d} z_{2\mathrm {B} }.$

This sixfold integral can be worked out and is a function of R ≡ R_AB. The result is shown in figure 2 (red curve). The curve shows a very shallow minimum, far less than the known bonding energy (≈ 104 kcal/mol). For shorter distances the curve is repulsive (has negative slope), which is due to the fact that the nucleus-nucleus repulsion is no longer screened by the electrons. Quantum mechanically, E₀ is the expectation value of the operator V (first-order energy) with respect to the product wave function φ_a(1)φ_b(2).

A deep quantum mechanical principle was ignored so far: electrons are indistinguishable particles. This may also be phrased as: permutations of electrons are symmetry operators. In this two-electron system there are only two permutations: I  ("doing nothing") and P (interchange of electron 1 and 2). It is known that eigenfunctions of Hamiltonians (which by definition commute with the symmetry operators) are adapted to the symmetry (technically: eigenfunctions belong to irreducible representations of the full symmetry group of the Hamiltonian). In the case at hand this means that H₂ wave functions (eigenfunctions of the H₂ Hamiltonian) have the properties

$I\psi _{\pm }(1,2)=\psi _{\pm }(1,2)\quad {\hbox{and}}\quad P\psi _{\pm }(1,2)=\pm \psi _{\pm }(1,2).$

The product wave function that gave rise to the energy E₀ lacks the second symmetry property, and therefore we try new approximate (zeroth-order) wave functions that are symmetry-adapted,

$\psi _{+}(1,2)={\sqrt {\frac {1}{2+2S^{2}}}}\;{\Big (}\phi _{a}(1)\phi _{b}(2)+\phi _{a}(2)\phi _{b}(1){\Big )}\quad {\hbox{and}}\quad \psi _{-}(1,2)={\sqrt {\frac {1}{2-2S^{2}}}}\;{\Big (}\phi _{a}(1)\phi _{b}(2)-\phi _{a}(2)\phi _{b}(1){\Big )},$

where the overlap integral S is given by

$S(R)=\int \phi _{a}(1)\phi _{b}(1)\;\mathrm {d} x_{1\mathrm {A} }\mathrm {d} y_{1\mathrm {A} }\mathrm {d} z_{1\mathrm {A} }.$

Clearly the function ψ₊ is symmetric and ψ₋ is antisymmetric under P. Both functions are normalized to unity thanks to the factors containing the square roots. According to quantum mechanical rules, the following expectation values (first-order energies), derived from properly symmetrized wave functions, give reasonable approximations to the exact energies,

$E_{+}(R)\equiv \langle \psi _{+}|V|\psi _{+}\rangle \quad {\hbox{and}}\quad E_{-}(R)\equiv \langle \psi _{-}|V|\psi _{-}\rangle .$

For conciseness the quantum mechanical bra-ket notation is used, for instance, the first braket:

$\langle \psi _{+}|V|\psi _{+}\rangle \equiv \int \int \psi _{+}(1,2)\;V\;\psi _{+}(1,2)\;\mathrm {d} x_{1\mathrm {A} }\mathrm {d} y_{1\mathrm {A} }\mathrm {d} z_{1\mathrm {A} }\mathrm {d} x_{2\mathrm {B} }\mathrm {d} y_{2\mathrm {B} }\mathrm {d} z_{2\mathrm {B} }.$

It is not difficult to show that

$E_{\pm }(R)={\frac {E_{0}\pm E_{1}}{1\pm S^{2}}}$

with

$E_{0}(R)=\langle \phi _{a}(1)\phi _{b}(2)|V|\phi _{a}(1)\phi _{b}(2)\rangle$

and

$E_{1}(R)=\langle \phi _{a}(1)\phi _{b}(2)|V|\phi _{a}(2)\phi _{b}(1)\rangle =\int \int \phi _{a}(1)\phi _{b}(2)\;V\;\phi _{b}(1)\phi _{a}(2)\;\mathrm {d} x_{1\mathrm {A} }\mathrm {d} y_{1\mathrm {A} }\mathrm {d} z_{1\mathrm {A} }\mathrm {d} x_{2\mathrm {B} }\mathrm {d} y_{2\mathrm {B} }\mathrm {d} z_{2\mathrm {B} }.$

The energy E₀ was discussed earlier, it arose from classical considerations, and it is small as long as the internuclear repulsion is screened by the electrons. New is the term E₁ which is negative and sizable and the denominator. The presence of E₁, often referred to as exchange term, has the consequence that E₋ is strongly repulsive for all R-values, while the energy E₊ shows a minimum of 0.232 E_H (the energy of the hydrogen atom), which is ≈ 73 kcal/mol, about 70% of the exact value. The position of the minimum is at 1.64 a₀ which is not far from the exact value 1.49 a₀.

It is important to emphasize that the exchange term appears because of the symmetry-adaptation of the zeroth-order wave function. In a classical approach, where electrons are distinguishable, there is no reason to symmetrize and the exchange term does not appear. To give an indication of the orders of magnitude we list the values at 1.60 a₀ (near the minimum):

S = 0.6972, E₀ = −0.0307, E₁ = −0.3132

At 1.6 a₀, the exchange term is an order of magnitude larger than the Coulomb term.

Remark

The Heitler-London theory is often put forward as a proof of the foresight of G. N. Lewis, who stressed the importance of electron pairs for chemical binding. As pointed out by Slater the hydrogen-molecule-cation H₂⁺, which has one electron, is bound by a mechanism that is very similar to the one responsible for binding in H₂. The main difference is that permutation symmetry is replaced by reflection symmetry. Hence one-electron bonds do exist.

Relation to electron spin

An electron has a spin up (spin function α) or spin down (spin function β). Two electrons can have four spin functions

$\alpha (1)\alpha (2),\quad \alpha (1)\beta (2),\quad \beta (1)\alpha (2),\quad \beta (1)\beta (2)$

These functions are not adapted to permutation symmetry. However, the following linear combinations are adapted

${\begin{aligned}\Theta _{-}^{0}&=\alpha (1)\beta (2)-\beta (1)\alpha (2)\\\Theta _{+}^{1}&=\alpha (1)\alpha (2)\\\Theta _{+}^{0}&=\alpha (1)\beta (2)+\beta (1)\alpha (2)\\\Theta _{+}^{-1}&=\beta (1)\beta (2)\\\end{aligned}}$

It can be shown that these functions are eigenfunctions of the spin angular momentum operators S_z and S². The one antisymmetric functions is known as a singlet function and the three symmetric functions are known as triplet functions.

Electrons are fermions, which means that their total wave functions (containing spin and space coordinates) must be antisymmetric under permutations. Clearly, the following products of space and spin functions are antisymmetric

${\begin{aligned}\psi _{-}(1,2)\Theta _{+}^{m}&\qquad (m=-1,\;0,\;1)\\\psi _{+}(1,2)\Theta _{-}^{0}&\end{aligned}}$

The following products are symmetric (would be valid functions if electrons were bosons, quod non),

${\begin{aligned}\psi _{+}(1,2)\Theta _{+}^{m}&\qquad (m=-1,\;0,\;1)\\\psi _{-}(1,2)\Theta _{-}^{0}\end{aligned}}$

We see that ψ₊ (with energy E₊) can only occur in conjunction with the spin singlet. The spin singlet state gives binding (sometimes very crudely and bordering to wrong expressed as "opposite spins attract"). The three triplet spin functions combine with ψ₋ (with repulsive energies E₋). Note that Θ⁰₊ also consists of two "opposite spins" and yet combines with the repulsive wave function negating the rule "opposite spins attract".