User talk:Paul Wormer/scratchbook1

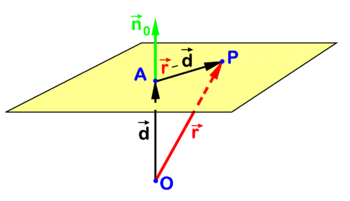
PD Image
Equation for plane.

Analytic geometry knows several closely related algebraic equations for a plane in three-dimensional Euclidean space. One such equation is illustrated in the figure. Point X is an arbitrary point in the plane and O (the origin) is outside the plane. The point A in the plane is chosen such that vector

${\overrightarrow {OA}}\equiv {\vec {\mathbf {a} }}$

is orthogonal to the plane. The vector

${\hat {\mathbf {n} }}\equiv {\frac {\vec {\mathbf {a} }}{a}}\quad {\hbox{with}}\quad a\equiv {|{\vec {\mathbf {a} }}|}$

is a unit (length 1) vector normal (perpendicular) to the plane. The following relation holds for an arbitrary point in the plane

$\left({\vec {\mathbf {r} }}-{\vec {\mathbf {a} }}\right)\cdot {\hat {\mathbf {n} }}=0\quad {\hbox{with}}\quad {\overrightarrow {OX}}\equiv {\vec {\mathbf {r} }}.$

Evidently a is the distance of O to the plane.

This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O,

${\vec {\mathbf {r} }}\cdot {\hat {\mathbf {n} }}={\vec {\mathbf {a} }}\cdot {\hat {\mathbf {n} }}\Longrightarrow xa_{x}+ya_{y}+za_{z}=a$

with

${\vec {\mathbf {a} }}=(a_{x},\;a_{y},\;a_{z}),\quad {\vec {\mathbf {r} }}=(x,\;y,\;z)$