Cartesian coordinates
In plane analytic geometry, Cartesian coordinates are two real numbers specifying a point in a plane (a 2-dimensional affine space). The coordinates are called after their originator Cartesius (the Latin name of René Descartes), who introduced them in 1637. In 3-dimensional analytic geometry, a point is given by three real numbers, also called Cartesian coordinates.
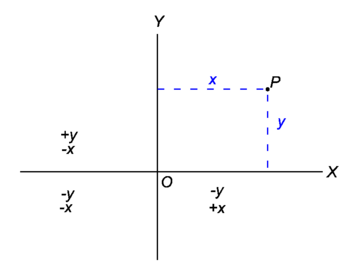
In two dimensions the position of a point P in a plane can be specified by its distance from two lines intersecting at right angles, called axes. For instance, in Figure 1 two lines intersect each other at right angles in the point O, the origin. One axis is the line O–X, the other O–Y, and any point in the plane can be denoted by two numbers giving its perpendicular distances from O–X and from O–Y.
A general point P can be reached by traveling a distance x along a line O–X, and then a distance y along a line parallel to O–Y. O–X is called the x-axis, O–Y the y-axis, and the point P is said to have Cartesian coordinates (x, y). In the coordinate system shown, as is indicated in the diagram, the x-coordinate is positive for points to the right of the y-axis and negative for points to the left of this axis. The y-coordinate is positive for points above the x-axis and negative for points below it. The coordinates of the origin are (0,0). One can introduce oblique axes and the position of a point may be defined in the same way: by its distance along lines parallel to the x and y axes. Sometimes these oblique coordinates also called "Cartesian", but more often the name is restricted to coordinates related to orthogonal axes.
Although orthogonal axes are frequently introduced in affine spaces of dimension n > 3, it is uncommon to refer to these coordinates as "Cartesian", usually they are called coordinates with respect to an orthogonal set of axes (briefly orthogonal coordinates).