User:John R. Brews/Fourier series
Fourier series (music)
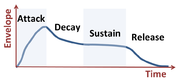
The amplitude of a musical note varies in time according to its sound envelope.[1]
The ideas of Fourier series have interesting application in music, for example, in illuminating the differences in pitch between musical instruments and in the construction of music synthesizers.[2] The frequency spectrum of a musical instrument playing a particular note varies with the instrument and with the way that it is played. The manner of playing determines the sound envelope of a note, and therefore the amplitude of its harmonics.[1]
Some instruments (like the flute or the violin) exhibit a fundamental frequency and its harmonics in varying amplitudes and phase, and others (like the cymbal or the drum) do not.[2][3]
Helmholtz' theory
A single note is often referred to as a tone, the lowest frequency present as the fundamental or prime partial tone and harmonics of this frequency that appear when a note is played on an instrument as harmonic upper partial tones or upper tones or partial tones. Where only one frequency is present, as with a tuning fork, it is called a simple tone:[4]
| It is well known that this union of several simple tones into one compound tone, which is naturally effected in the tones produced by most musical instruments, is artificially imitated on the organ by peculiar mechanical contrivances. The tones of organ-pipes are comparatively poor in upper partials. When it is desirable to use a stop of incisive penetrating quality of tone and great power, the wide pipes (principal register and wiethgedackt) are not sufficient their tone is too soft too defective in upper partials; and the narrow pipes (geigen-register and quitaten) are also unsuitable, because, although more incisive, their tone is weak,. For such occasions, then as in accompanying congregational singing, recourse is had to the compound stops. In these stops every key is connected with a large or smaller series of pipes, which it opens simultaneously, and which give the prime tone and a certain number of the first upper partials of the compound tone of the note in question. Helmholtz, p. 91[4] |
References
- ↑ 1.0 1.1 Stanley R. Alten (2010). “Sound envelope”, Audio in Media, 12th ed. Cengage Learning, p. 13. ISBN 049557239X.
- ↑ 2.0 2.1 Leon Gunther (2011). The Physics of Music and Color. Springer, p. 47 ff. ISBN 1461405564.
- ↑ Bart Hopkin (1996). “Figure 2-4”, Musical Instrument Design: Practical Information for Instrument Making. See Sharp Press, p. 110. ISBN 1884365086.
- ↑ 4.0 4.1 Hermann Ludwig F. von Helmholtz (1875). On the sensations of tone as a physiological basis for the theory of music, Translation by Alexander John Ellis. Oxford University Press, p. 33.
- Thomas D. Rossing (2007). Springer Handbook of Acoustics. Springer, p. 541. ISBN 0387304460.