Reflection (geometry)

In analytic geometry, a reflection is a linear operation σ on $\mathbb {R} ^{3}$ with σ² = 1. This property of σ is called involution. An involutory operator is non-singular and σ⁻¹ = σ. Reflecting twice an arbitrary vector brings back the original vector :

$\sigma ({\vec {\mathbf {r} }}\,)={\vec {\mathbf {r} }}\,'\quad {\hbox{and}}\quad \sigma ({\vec {\mathbf {r} }}\,'\,)={\vec {\mathbf {r} }}.$

The operation σ is orthogonal, which means that it preserves inner products and that its inverse is equal to its adjoint,

$\sigma ^{\mathrm {T} }=\sigma ^{-1}\;(=\sigma ).\,$

Hence reflection is also symmetric: σ^T = σ. Orthogonal operators have determinant ±1. Those with positive determinant are rotations, while reflections have determinant −1. Because σ is symmetric it has real eigenvalues; since it is orthogonal its eigenvalues have modulus 1. It follows that its eigenvalues are ±1. The product of the eigenvalues being the determinant, −1, the eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is equal to minus the identity operator, this operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the former set of eigenvalues is reflection in a plane. Reflections in a plane are the subject of this article.

PD Image
Fig. 1. The vector $\scriptstyle {\vec {\mathbf {r} }}$ goes to $\scriptstyle {\vec {\mathbf {r} }}'$ under reflection in a plane. The unit vector $\scriptstyle {\hat {\mathbf {n} }}$ is normal to mirror plane.

Reflection in a plane

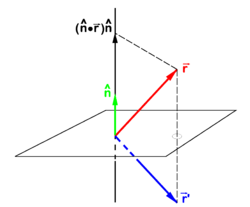
If ${\hat {\mathbf {n} }}$ is a unit vector normal (perpendicular) to a plane—the mirror plane—then $({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\hat {\mathbf {n} }}$ is the projection of ${\vec {\mathbf {r} }}$ on this unit vector. From the figure it is evident that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{r}} - \vec{\mathbf{r}}\,' = 2 (\hat{\mathbf{n}}\cdot\vec{\mathbf{r}})\, \hat{\mathbf{n}} \;\Longrightarrow\; \vec{\mathbf{r}}\,' = \vec{\mathbf{r}} - 2 (\hat{\mathbf{n}}\cdot\vec{\mathbf{r}})\hat{\mathbf{n}} }

If a non-unit normal Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{n}}} is used then substitution of

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbf{n}} = \frac{\vec{\mathbf{n}}}{ |\vec{\mathbf{n}}|} \equiv \frac{\vec{\mathbf{n}}}{n} }

gives the mirror image,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{r}}\,' = \vec{\mathbf{r}} - 2 \frac{ (\vec{\mathbf{n}}\cdot\vec{\mathbf{r}})\vec{\mathbf{n}}}{n^2} }

Sometimes it is convenient to write this as a matrix equation. Introducing the dyadic product, we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{r}}\,' = \left[ \mathbf{E} - \frac{2}{n^2} \vec{\mathbf{n}} \otimes\vec{\mathbf{n}} \right] \; \vec{\mathbf{r}}, }

where E is the 3×3 identity matrix.

Dyadic products satisfy the matrix multiplication rule

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\vec{\mathbf{a}}\otimes\vec{\mathbf{b}}]\, [ \vec{\mathbf{c}}\otimes\vec{\mathbf{d}}] = (\vec{\mathbf{b}} \cdot \vec{\mathbf{c}}) \big( \vec{\mathbf{a}}\otimes\vec{\mathbf{d}} \big). }

By the use of this rule it is easily shown that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \mathbf{E} - \frac{2}{n^2} \vec{\mathbf{n}} \otimes\vec{\mathbf{n}} \right]^2 = \mathbf{E}, }

which confirms that reflection is involutory.

PD Image
Fig. 2. The vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{s}}} goes to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{s}}\,'} under reflection

Reflection in a plane not through the origin

In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{t}}} . The length of this vector is the distance from O to the plane. From Figure 2, we find

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{r}} = \vec{\mathbf{s}} - \vec{\mathbf{t}}, \quad \vec{\mathbf{r}}\,' = \vec{\mathbf{s}}\,' - \vec{\mathbf{t}} }

Use of the equation derived earlier gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{s}}\,' - \vec{\mathbf{t}} = \vec{\mathbf{s}} - \vec{\mathbf{t}} - 2 \big(\hat{\mathbf{n}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})\big)\hat{\mathbf{n}}. }

And hence the equation for the reflected pair of vectors is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{s}}\,' = \vec{\mathbf{s}} - 2 \big(\hat{\mathbf{n}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})\big)\hat{\mathbf{n}}, }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbf{n}}} is a unit normal to the plane. Obviously Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{t}}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbf{n}}} are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{t}}} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{s}}\,' = \vec{\mathbf{s}} - 2 \frac{\vec{\mathbf{t}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})}{t^2}\vec{\mathbf{t}}, \quad t^2 \equiv \vec{\mathbf{t}}\cdot \vec{\mathbf{t}}. }

Two consecutive reflections

PD Image
Fig. 3. Two reflections. Left drawing: 3-dimensional drawing. Right drawing: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect the line PQ in the point P′

Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.

It is obvious that the product of two reflections is a rotation. Indeed, a reflection is orthogonal and has determinant −1. The product of two orthogonal operators is again orthogonal and the rule for determinants is det(AB) = det(A)det(B), so that the product of two reflections is an orthogonal operator with unit determinant, i.e., a rotation.

Let the normal of the first plane be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{s}}} and of the second Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbf{t}}} , then the rotation is represented by the matrix

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \mathbf{E} - \frac{2}{t^2} \vec{\mathbf{t}} \otimes\vec{\mathbf{t}} \right]\, \left[ \mathbf{E} - \frac{2}{s^2} \vec{\mathbf{s}} \otimes\vec{\mathbf{s}} \right] = \mathbf{E} - \frac{2}{t^2} \vec{\mathbf{t}} \otimes\vec{\mathbf{t}} - \frac{2}{s^2} \vec{\mathbf{s}} \otimes\vec{\mathbf{s}} + \frac{4}{t^2 s^2} (\vec{\mathbf{t}}\cdot\vec{\mathbf{s}})\; \big(\vec{\mathbf{t}} \otimes\vec{\mathbf{s}}\big) }

The (i,j) element if this matrix is equal to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{ij} - \frac{2 t_i t_j }{t^2} - \frac{2 s_i s_j }{s^2} + \frac{4 t_i s_j (\sum_k t_k s_k)}{t^2 s^2} }