Electric displacement

In physics, the electric displacement, usually denoted by D, is a vector field in a non-conducting medium, a dielectric. The displacement D is proportional to the electric field E in which the dielectric is placed. In SI units,

$\mathbf {D} (\mathbf {r} )=\epsilon _{0}\epsilon _{r}\mathbf {E} (\mathbf {r} ),$

where ε₀ is the electric constant and ε_r is the relative permittivity. In Gaussian units ε₀ does not occur and may put equal to unity. In vacuum the dimensionless quantity ε_r = 1 (both for SI and Gaussian units) and D is simply related (SI), or equal (Gaussian), to E. Often D is termed an auxiliary field with E the principal field. An other auxiliary field is the electric polarization P of the dielectric,

${\begin{aligned}\mathbf {P} &\equiv \mathbf {D} -\epsilon _{0}\mathbf {E} &\mathrm {(SI)} \\\mathbf {P} &\equiv (\mathbf {D} -\mathbf {E} )/4\pi &\mathrm {(Gaussian)} \\\end{aligned}}$

The vector field P describes the polarization (displacement of charges) occurring in a chunk of dielectric when it is brought into an electric field. The fact that for any insulator ε_r > 1 (i.e., that D is not simply equal to ε₀E) has as its cause the polarization of the dielectric.

The electric displacement appears in one of the macroscopic Maxwell equations,

${\boldsymbol {\nabla }}\cdot \mathbf {D} (\mathbf {r} )=\rho (\mathbf {r} ),$

where the symbol ∇⋅ gives the divergence of D(r) and ρ(r) is the charge density at the point r.

Relation of D to surface charge density σ

Two capacitors at same voltage V. On the left vacuum between the plates and on the right a dielectric with relative permittivity ε_r. Absolute values of surface charge densities are indicated by σ.

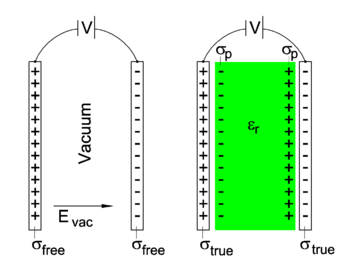
In the special case of a parallel-plate capacitor, often used to study and exemplify problems in electrostatics, the electric displacement D is easy to visualize. In this example D (the magnitude of vector D) is equal to the true surface charge density  σ_true   (the surface density on the plates of the right-hand capacitor in the figure). In this figure two parallel-plate capacitors are shown that are identical, except for the matter between the plates: on the left no matter (vacuum), on the right a dielectric. Note in particular that the plates have the same voltage difference V and the same area A.

To explain that D = σ_true, we recall that the relative permittivity may be defined as the ratio of two capacitances of parallel-plate capacitors, (capacitance is total charge on the plates divided by voltage difference). Namely, the relative permittivity is the ratio of the capacitance C of the capacitor filled with dielectric to the capacitance C_vac of a capacitor in vacuum,

$\epsilon _{\mathrm {r} }\equiv {\frac {C}{C_{\mathrm {vac} }}}={\frac {Q_{\mathrm {true} }}{V}}\left[{\frac {Q_{\mathrm {free} }}{V}}\right]^{-1}={\frac {Q_{\mathrm {true} }}{Q_{\mathrm {free} }}}={\frac {\sigma _{\mathrm {true} }}{\sigma _{\mathrm {free} }}}\quad \Longrightarrow \quad \sigma _{\mathrm {true} }=\epsilon _{\mathrm {r} }\sigma _{\mathrm {free} },$

where we used that Q is σ × A, with A the area of the plates. Clearly, the charge density on the plates increases by a factor ε_r when the dielectric is moved in between the plates.

The extra charge on the plates is compensated by the polarization of the dielectric, that is, the build-up of a positive polarization surface charge density σ_p on the side of the negative plate and a negative surface charge density on the positive side. Note, parenthetically, that only the absolute values of the charge densities are indicated and that the vectors E_vac and D are parallel. The total charge is conserved, for instance on the side of the positively charged plate:

$\sigma _{\mathrm {free} }=\sigma _{\mathrm {true} }-\sigma _{\mathrm {p} }.\,$

(Here the minus sign appears because the polarization charge density σ_p is negative on the positive side of the capacitor).

Assuming that the plates are very much larger than the distance between the plates, we may apply the following formula for E_vac (the magnitude of the vector E_vac),

$E_{\mathrm {vac} }={\frac {\sigma _{\mathrm {free} }}{\epsilon _{0}}}.$

(This electric field strength does not depend on the distance of a field point to the plates: the electric field between the plates is homogeneous.) Now

$D\equiv \epsilon _{0}\epsilon _{\mathrm {r} }E_{\mathrm {vac} }=\epsilon _{\mathrm {r} }\sigma _{\mathrm {free} }=\sigma _{\mathrm {true} }\,.$

It is of some interest to note that the polarization vector P (pointing from minus to plus polarization charges, i.e., parallel to E_vac) has magnitude P equal to the polarization surface charge density σ_p. Indeed, the magnitudes of the three parallel vectors are related by,

$P\equiv D-\epsilon _{0}E_{\mathrm {vac} }=\sigma _{\mathrm {true} }-\sigma _{\mathrm {free} }=\sigma _{\mathrm {p} }.$

Tensor character of relative permittivity

As defined above, D and E are parallel, i.e., ε_r is a number (a scalar). For a non-isotropic dielectric ε_r may be a second rank tensor,

$D_{i}(\mathbf {r} )=\epsilon _{0}\sum _{j=1}^{3}(\epsilon _{r})_{ij}E_{j}(\mathbf {r} ),\quad i,j=1,2,3=x,y,z,$

so that D and E are not necessarily parallel.