Euclid's Elements
Euclid's Elements is the oldest systematic treatise on geometry. For more than twenty centuries the Elements was the major textbook model in the study and teaching of mathematics. Also in other fields Euclid's work led the way. The philosopher Spinoza wrote his work Ethics along the lines of the Elements and so did the physicist Newton when he composed his opus magnum Principia.
The Elements is often considered as one of the documents, next to the Bible, that had the most impact on the Western culture. However, according to modern mathematical standards of rigor, the Elements show some shortcomings. These have been repaired as late as the 1890s by the German mathematician Hilbert.
Contents
The work consists of thirteen Books. The books I-V are devoted to planar geometry and the books XI-XIII to stereometry. The other books deal with the geometric foundation of the properties of numbers.
Book I starts with definitions of the type: a point is that which has no part and: a line is a breadthless length. It then goes on to the formulation of the five postulates (evident assumptions, axioms) of Euclidean geometry:
- It is possible to draw a straight line from any point to any point.
- It is possible to extend a finite straight line continuously in a straight line.
- It is possible to describe a circle with any center and distance (radius).
- All right angles are equal to one another.
- If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than the two right angles.
The first 28 propositions (theorems) are based on the above postulates, and treat mainly congruence of triangles and of other geometric figures.
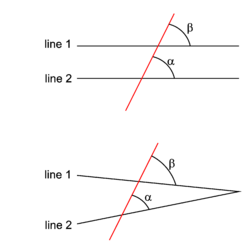
One of the most famous propositions is the sixteenth which states that the exterior angle of a triangle is greater than either remote interior angle. See the lower part of the figure on the right, where angle β is larger than angle α by virtue of Euclid's sixteenth proposition.
The sixteenth proposition, together with the fifth postulate, implies the existence of parallel lines, see the upper part of the figure. Indeed, one can prove that if a straight line (the red one) falling on two other straight lines makes two alternate angles that are equal (α = β), then the two straight lines must be parallel. Euclid realized that this result could not be proven on basis of his first four postulates, and therefore he added his fifth most famous postulate. In the present case the fifth postulate reads: if β > α then line 1 and line 2 must cross. To see that this statement is indeed the fifth postulate, we call γ the supplementary angle adjacent to β. That is, β+γ = 1800. The fifth postulate states that if α+γ < 1800 then line 1 and line 2 cross on the side where that is the case. Now,
and since β ≡ 1800−γ we see that the statement: if β > α then line 1 and line 2 cross, is indeed Euclid's fifth postulate. By proposition 16 and postulate 5 it follows that line 1 and line 2 cross if and only if β > α. Hence the lines do not cross (are parallel) if and only if α = β. (Note that the case β < α is covered by interchanging α and β.)
For many centuries workers have tried to prove the fifth postulate from the other four, but all attempts failed. Indeed, a geometry—a non-Euclidean geometry—without this postulate is possible and logically consistent (in contrast to, for instance, Immanuel Kant's view, who gave a philosopher's proof of the necessity of Euclidean geometry).
Another famous proposition in Book I is number 47: the Pythagorean theorem, which is proved by a technique still used in high school texts.
Book II is on geometrical algebra. The Greeks did not know irrational numbers and so could not handle all lengths, areas, angles, and volumes numerically. Therefore all all quantities in Book II are handled geometrically. Numbers are represented by line segments and products of numbers by areas. Most of division is postponed to Book V.
Book III is about circles, chords, inscribed angles and so on.
Book IV deals with figures inscribed in an circumscribed about circles. For example, triangles, squares, regular pentagons and hexagons.
Book V is probably the most important of the books. It is based on Eudoxus' work on proportions. It is about ratios, including incommensurable ratios, but avoids irrational numbers. The emphasis is on proportions for all kinds of magnitudes. Book V proves twenty-five theorems about magnitudes and ratios of magnitudes.
Book VI, about similar figures, uses the theory of Book V.
Book VII, VIII, and IX treat the theory of numbers, that is, the properties of whole numbers and ratios of whole numbers. These three books are the only ones in the Elements that treat arithmetic as such.
Book X tries to classify types of irrationals—magnitudes incommensurable with given magnitudes.
Book XI, XII, and XIII are on solid geometry, a solid being that which has length, breadth and depth. Surfaces are the extremities of solids. Discussed are, among others, pyramid, prism, sphere, cone, cylinder, cube, the regular octahedron, and the regular icosahedron. Book XII treats the method of exhaustion, the word stemming from the seventeenth century when exhaustion was the immediate forerunner of integration.
The thirteen books of the Elements contain 467 propositions (theorems).
Bibliography
- Artmann, Benno. Euclid - The Creation of Mathematics (2001) excerpt and text search
- Cajori, Florian. A History of Mathematics (1919) complete text online free
- Euclid. The Thirteen Books of Euclid's Elements, Books 1 and 2 ed. by Thomas L. Heath (1956) excerpt and text search
- Kline, Morris. Mathematical Thought from Ancient to Modern Times, (1972). excerpt and text search
- Mueller, Ian. Philosophy of Mathematics and Deductive Structure in Euclid's Elements (1981).