Spherical polar coordinates

Spherical polar coordinates

In mathematics and physics, spherical polar coordinates (also known as spherical coordinates) form a coordinate system for the three-dimensional real space $\scriptstyle \mathbb {R} ^{3}$. Three numbers, two angles and a length specify any point in $\scriptstyle \mathbb {R} ^{3}$. The two angles specify the position on the surface of a sphere and the length gives the radius of the sphere.

Spherical polar coordinates are useful in cases where there is (approximate) spherical symmetry, in interactions or in boundary conditions (or in both). In such cases spherical polar coordinates often allow the separation of variables simplifying the solution of partial differential equations and the evaluation of three-dimensional integrals.

Definition

Let x, y, z be Cartesian coordinates of a vector $\scriptstyle {\vec {\mathbf {r} }}$ in $\scriptstyle \mathbb {R} ^{3}$, that is,

${\vec {\mathbf {r} }}=({\vec {\mathbf {e} }}_{x},\,{\vec {\mathbf {e} }}_{y},\,{\vec {\mathbf {e} }}_{z}){\begin{pmatrix}x\\y\\z\\\end{pmatrix}}\equiv x\,{\vec {\mathbf {e} }}_{x}+y\,{\vec {\mathbf {e} }}_{y}+z\,{\vec {\mathbf {e} }}_{z},$

where $\scriptstyle {\vec {\mathbf {e} }}_{x},\,{\vec {\mathbf {e} }}_{y},\,{\vec {\mathbf {e} }}_{z}$ are unit vectors along the x, y, and z axis, respectively. The x, y, and z axes are orthogonal and so are the unit vectors along them.

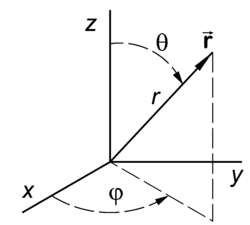
The length r of the vector $\scriptstyle {\vec {\mathbf {r} }}$ is one of the three numbers necessary to give the position of the vector in three-dimensional space. By applying twice the theorem of Pythagoras we find that r² = x² + y² + z².

Let θ be the colatitude angle (see the figure) of the vector $\scriptstyle {\vec {\mathbf {r} }}$. In the usual system to describe a position on Earth, latitude has its zero at the equator, while the colatitude angle, introduced here, has its zero at the "North Pole". That is, the angle θ is zero when $\scriptstyle {\vec {\mathbf {r} }}$ is along the positive z-axis. The sum of latitude and colatitude of a point is 90⁰; these angles being complementary explains the name of the latter.

The angle φ gives the angle with the x-axis of the projection $\scriptstyle {\vec {\mathbf {r} }}'$ of $\scriptstyle {\vec {\mathbf {r} }}$ on the x-y plane. The angle φ is the longitude angle (also known as the azimuth angle).

Note that the projection $\scriptstyle {\vec {\mathbf {r} }}'$ has length r sinθ. The length of the projection of $\scriptstyle {\vec {\mathbf {r} }}'$ on the x and y axis is therefore r sinθcosφ and r sinθsinφ, respectively. In summary, the spherical polar coordinates r, θ, and φ of $\scriptstyle {\vec {\mathbf {r} }}$ are related to its Cartesian coordinates by

${\begin{aligned}x&=r\sin \theta \cos \phi \\y&=r\sin \theta \sin \phi \\z&=r\cos \theta \end{aligned}}$

Given a spherical polar triplet (r, θ, φ) the corresponding Cartesian coordinates are readily obtained by application of these defining equations.

The figure makes clear that 0⁰ ≤ φ ≤ 360⁰, 0⁰ ≤ θ ≤ 180⁰, and r > 0. The coordinate surfaces are:

1. r constant, all θ and φ: surface of sphere.
2. θ constant, all r and φ: surface of a cone.
3. φ constant, all r and θ: plane.

The computation of spherical polar coordinates from Cartesian coordinates is somewhat more difficult than the converse, due to the fact that the spherical polar coordinate system has singularities, also known as points of indeterminacy. The first such point is immediately clear: if r = 0, we have a zero vector (a point in the origin). Then θ and φ are undetermined, that is to say, any values for these two parameters will give the correct result x = y = z = 0. Compare this to the case that one of the Cartesian coordinates is zero, say x = 0, then the other two coordinates are still determined (they fix a point in the yz-plane). Two other points of indeterminacy are the "North" and the "South Pole", θ = 0⁰ and θ = 180⁰, respectively (while r ≠ 0). On both poles the longitudinal angle φ is undetermined.

So, when going from Cartesian coordinates to spherical polar coordinates, one has to watch for the singularities, especially when the transformation is performed by a computer program. Given x, y and z, the consecutive steps are

${\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arccos(z/r),\quad r\neq 0\\r'&=r\sin \theta ={\sqrt {x^{2}+y^{2}}}\\\phi &={\begin{cases}\arccos(x/r')&\quad {\hbox{if}}\quad y\geq 0,\quad r'\neq 0\\360^{0}-\arccos(x/r')&\quad {\hbox{if}}\quad y<0,\quad r'\neq 0\\\end{cases}}\end{aligned}}$

Other conventions

(To be continued)