Fixed point of logarithm: Difference between revisions
imported>Dmitrii Kouznetsov (load) |
imported>Dmitrii Kouznetsov (add pic) |
||
| Line 1: | Line 1: | ||
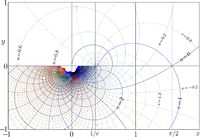
[[File:FilogbigT.jpg|300px|right|thumb|[[Complex map]] of function <math>f=\mathrm{Filog}(x+\mathrm i y)</math>]] | [[File:FilogbigT.jpg|300px|right|thumb|[[Complex map]] of function <math>f=\mathrm{Filog}(x+\mathrm i y)</math>]] | ||
[[File:FilogmT1000a.jpg|200px|right|thumb|Zoom-in from the central part of the previous figure]] | |||
'''[[Fixed point]]s of [[logarithm]]''' to base <math>b</math> are solutions <math>L</math> of equation | '''[[Fixed point]]s of [[logarithm]]''' to base <math>b</math> are solutions <math>L</math> of equation | ||
: <math>\!\!\!\!\! (1) ~ ~ ~ \displaystyle L=\log_b(L) </math> | : <math>\!\!\!\!\! (1) ~ ~ ~ \displaystyle L=\log_b(L) </math> | ||
| Line 21: | Line 22: | ||
where asterisk (*) denotes the [[complex conjugation]]. | where asterisk (*) denotes the [[complex conjugation]]. | ||
The complex map of function <math>\mathrm{Filog}</math> is shown in the figure at right. | The complex map of function <math>\mathrm{Filog}</math> is shown in the top figure at right. | ||
<math>f=\mathrm{Filog}(x+\mathrm i y)</math> is shown in the <math>x,y</math> plane with | <math>f=\mathrm{Filog}(x+\mathrm i y)</math> is shown in the <math>x,y</math> plane with | ||
levels <math>u=\Re(f)=\rm const</math> and | levels <math>u=\Re(f)=\rm const</math> and | ||
levels <math>v=\Im(f)=\rm const</math> | levels <math>v=\Im(f)=\rm const</math>. The next figure shows the zoom-in of the central part. | ||
==Relation to the LambertW function== | ==Relation to the LambertW function== | ||
Revision as of 21:05, 7 March 2013
Fixed points of logarithm to base are solutions of equation
The special name Filog (Fixed point of logarithm) is suggested for the function that expresses one of these solutions through the logarithm of the base [1];
where and is Tania function, id est, solution of the equation
with
the prime denotes the derivative.
Then, another fixed point can be expressed as follows:
where asterisk (*) denotes the complex conjugation.
The complex map of function is shown in the top figure at right. is shown in the plane with levels and levels . The next figure shows the zoom-in of the central part.
Relation to the LambertW function
While the real part of the base is positive, the fixed point of logarithm can be expressed also through the LambertW function.
Both fixed points in the whole complex plane of values of base may be neecessary; then, the representation (3) through the Tania function is more convenient than that through the LambertW; the efficient algorithm for evaluation of the Tania function is available [2].
Application of the fixed points of logarithm
The efficient evaluation of the fixed points of logarithm is important for the construction and evaluation of the tetration to the complex base. The tetration approaches values or as the imaginary part of the argument becomes large.