Diffraction: Difference between revisions
imported>Johan Förberg (→Theory: General structure in place) |
imported>Johan Förberg |
||
| Line 18: | Line 18: | ||
=== The circular opening === | === The circular opening === | ||
=== The double slit === | === The double slit === | ||
Revision as of 14:26, 21 October 2010
Diffraction is a physical phenomenon wdue to which waves passing through small openings will tend to 'bend' towards the edges. Diffraction applies to virtually all kinds of waves including sound, light, and other electromagnetic waves such as radio waves). The phenomenon is particularily interesting because of the interference patterns that arise from such waves. It also puts a limit to the theoretical resolution of optical systems. It is also a convincing piece of evidence for the wave nature of light.
Simple cases
The single slit
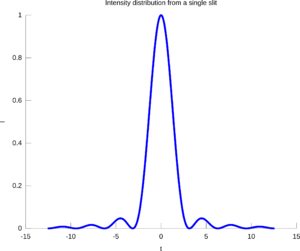
The simplest example of diffraction is the single slit experiment. A laser is set up pointing against a small rectangular slit in an otherwise opaque screen. Some distance behind the slit is a screen on which the diffraction pattern can be observed. The slit has a width b and a height which is large in comparison with b, and the components are sufficiently far away from each other that the waves can be seen as plane (having straight wavefronts). On the screen we observe a pattern of 'dots', with an intense central maximum in the middle and auxiliary maxima on both sides of it, intensity rapidly decreasing as we move away from the centre. We note that the central maximum is twice as wide as the others. If the width b of the slit is made smaller, the pattern will spread out in the horizontal direction. After application of the principle of superposition, we arrive at the following formula for the n:th minimum:
Where b is the width of the slit, θ is the angle made with the line which goes straight through unaffected, n is a whole number excluding 0, and λ is the wavelength of the diffracted wave. We also obtain an expression for the intensity in a point at angle θ:
The circular opening
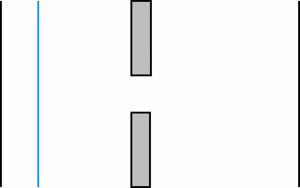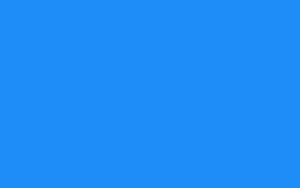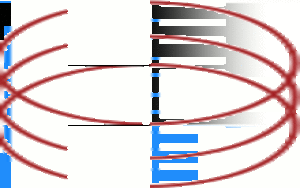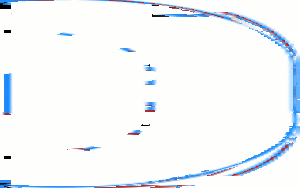
The double slit
Young's double slit experiment
Diffraction gratings
Theory
Huygen's principle
Waves obey Huygen's principle, which states that all points on a wave front can be seen as sources for new, circular elementary waves. This implies that waves will 'bend around' objects that are in their way, and will also bend around corners that they pass. Think of a wave in a water surface, and how it behaves when meeting a pole that rests in the water. It is a fact that the amount of bending varies with the wavelength, such that longer wavelengths bend more strongly. For that reason, your voice appears darker to you than to others, because more of the lower sounds (longer wavelengths) will bend around your head and reach your ears.
Babinet's principle
Complimentary patterns
Resolution and the Rayleigh criterion
The Rayleigh criterion, camera example
Geometric interpretation
Derivation of the single-slit formula
Quantum-mechanical interpretation
Heisenberg's uncertainty principle
Applications
Spectrographs, ...