Diffraction

Diffraction is a physical phenomenon due to which waves passing through small openings will tend to 'bend' towards the edges. Diffraction applies to virtually all kinds of waves including sound, light, and other electromagnetic waves (such as radio waves). The phenomenon is particularly interesting because of the interference patterns that arise from such waves. It puts a limit to the theoretical resolution of optical systems. It is also a convincing piece of evidence for the wave nature of light.

Simple cases

The single slit

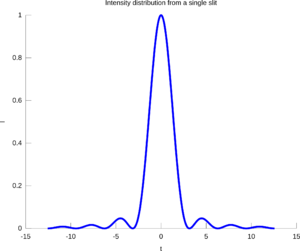
The simplest example of diffraction is the single slit experiment. A laser is set up pointing against a small rectangular slit in an otherwise opaque screen. Some distance behind the slit is a screen on which the diffraction pattern can be observed. The slit has a width b and a height which is large in comparison with b, and the components are sufficiently far away from each other that the waves can be seen as plane (having straight wavefronts). On the screen we observe a pattern of 'dots', with an intense central maximum in the middle and auxiliary maxima on both sides of it, intensity rapidly decreasing as we move away from the centre. We note that the central maximum is twice as wide as the others. If the width b of the slit is made smaller, the pattern will spread out in the horizontal direction. After application of the principle of superposition, we arrive at the following formula for the n:th minimum:

$b\sin \theta =n\lambda \!$

Where b is the width of the slit, θ is the angle made with the line which goes straight through unaffected, n is a whole number (integer) excluding 0, and λ is the wavelength of the diffracted wave. We also obtain an expression for the intensity in a point at angle θ:

(CC) Diagram: Johan A. Förberg
The intensity pattern from a single slit.

$I=I_{0}{\frac {\sin ^{2}\beta }{\beta ^{2}}},\qquad \beta ={\frac {b\pi \sin \theta }{\lambda }}$

The double slit

Young's double slit experiment

Theory

(CC) Diagram: Johan A. Förberg
Huygen's principle applied to a wave passing a small opening. The blue lines are wavefronts.

Huygen's principle

Waves obey Huygen's principle, which states that all points on a wave front can be seen as sources for new, circular elementary waves. This implies that waves will 'bend around' objects that are in their way, and will also bend around corners that they pass. Think of a wave in a water surface, and how it behaves when meeting a pole that rests in the water. It is a fact that the amount of bending varies with the wavelength, such that longer wavelengths bend more strongly. For that reason, your voice appears darker to you than to others, because more of the lower sounds (longer wavelengths) will bend around your head and reach your ears.

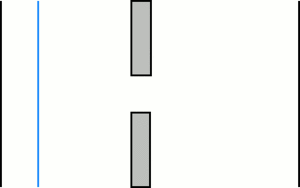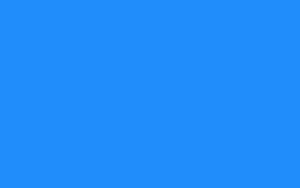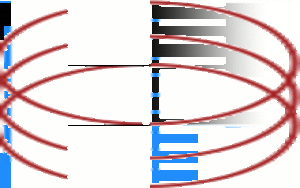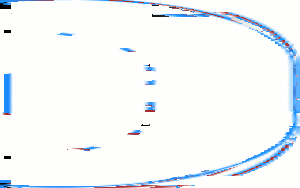
Babinet's principle and complimentary patterns

File:Complimentary-patterns.svg

(CC) Drawing: Johan A. Förberg
Two pairs of complimentary patterns.

A complimentary pattern is the inverse of a pattern, so to speak. If P is a pattern that has some opaque areas and some transparent ones, the complimentary pattern P' is the pattern in which exactly the opposite areas are opaque and transparent. Thus, the complimentary pattern of a single slit is a thread of the same size, and the complimentary pattern of a circular opening is a dot.

If P and P' are complimentary patterns, Babinet's principle states that the intensity distributions from these are identical. The reasoning behind this is that complimentary patterns together add up to a completely opaque pattern. This means that the diffracted waves from these patterns must add up to zero, implying that waves from these patterns have equal amplitude in each point, but are completely out of phase. The phase of a wave is not visible in an intensity distribution, why the distributions are equal.

Scientists were initially sceptical about this law, since it predicts a bright spot in the middle of the diffraction pattern from, say, a coin of the correct size. This spot was later observed. It matters, however that the pattern is of the correct size depending on the wavelength of the waves used.

Resolution and the Rayleigh criterion

The Rayleigh criterion, camera example

Geometric interpretation

Derivation of the single-slit formula

Quantum-mechanical interpretation

Heisenberg's uncertainty principle

Applications

Spectrographs, ...