Work (physics): Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer |
||
| Line 8: | Line 8: | ||
== Definition of mechanical work == | == Definition of mechanical work == | ||
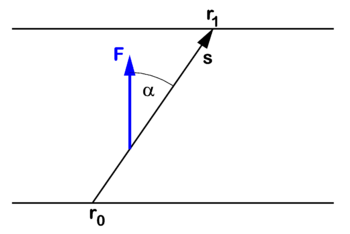
{{Image|Work with constant force.png|right|350px|Constant force '''F''' along path '''s''' <nowiki>=</nowiki> '''r'''<sub>1</sub> − '''r'''<sub>0</sub>.}} | {{Image|Work with constant force.png|right|350px|Constant force '''F''' along path '''s''' <nowiki>=</nowiki> '''r'''<sub>1</sub> − '''r'''<sub>0</sub>.}} | ||
The mechanical work ''W'' is defined as force times path length: When a ''constant'' force '''F''' acts on a body along a ''straight'' path and the body is moved over a length |'''s'''| along this path, then | |||
:<math> | :<math> | ||
W=\mathbf F \cdot \mathbf s = |\mathbf F| \, |\mathbf s| \, \cos\alpha\,. | W=\mathbf F \cdot \mathbf s = |\mathbf F| \, |\mathbf s| \, \cos\alpha\,. | ||
| Line 16: | Line 16: | ||
When the force is directed along the path ('''F''' and '''s''' parallel), α = 0, cosα = 1, and we have simply ''W'' = |'''F'''| |'''s'''|. The positive work ''W'' is converted into an increase of [[kinetic energy]] ''T'', | When the force is directed along the path ('''F''' and '''s''' parallel), α = 0, cosα = 1, and we have simply ''W'' = |'''F'''| |'''s'''|. The positive work ''W'' is converted into an increase of [[kinetic energy]] ''T'', | ||
:W = Δ''T'' ≡ ''T''<sub>1</sub> − ''T''<sub>0</sub> > 0. | :W = Δ''T'' ≡ ''T''<sub>1</sub> − ''T''<sub>0</sub> > 0. | ||
In the next section this relation will be proved and shown to be a consequence of [[Newton's second law]]: ''F = m a''. | |||
When a force is perpendicular to the path, α = 90°, cosα = 0, the force performs no work. Examples of such a situation are the [[centrifugal force]] on a mass in uniform circular motion and the gravitational force acting on a satellite in a circular orbit. If a body is in uniform (i.e., has constant speed) straight motion and the only force acting on it is perpendicular to its path, then the body will persist in its uniform straight motion ([[Newton's first law]]). | When a force is perpendicular to the path, α = 90°, cosα = 0, the force performs no work. Examples of such a situation are the [[centrifugal force]] on a mass in uniform circular motion and the gravitational force acting on a satellite in a circular orbit. If a body is in uniform (i.e., has constant speed) straight motion and the only force acting on it is perpendicular to its path, then the body will persist in its uniform straight motion ([[Newton's first law]]). | ||
Revision as of 05:13, 4 July 2009
In physics, work is the energy that is transferred to a body when it is moved along a path by a force. When the force is conservative (non-dissipative) the work is independent of the path. Work done on a body is accomplished not only by a displacement of the body as a whole from one place to another but also, for example, by compressing a gas, by rotating a shaft, and even by directing small magnetic particles within a body along an external magnetic field.
As stated, work is a form of energy and consequently has dimension energy (force times length). In SI units the unit is joule; in cgs units it is erg.
The terms "work", "energy", and "force" have a well-defined, quantitative, meaning in physics, which differs somewhat from their more qualitative meaning in daily life. For instance, in physics work can be negative.
Definition of mechanical work
The mechanical work W is defined as force times path length: When a constant force F acts on a body along a straight path and the body is moved over a length |s| along this path, then
Here s is vector of magnitude |s| along the path. The dot product between the two vectors F and s is the product of their magnitudes |F| and |s| times the cosine of the angle, α, between the vectors.
When the force is directed along the path (F and s parallel), α = 0, cosα = 1, and we have simply W = |F| |s|. The positive work W is converted into an increase of kinetic energy T,
- W = ΔT ≡ T1 − T0 > 0.
In the next section this relation will be proved and shown to be a consequence of Newton's second law: F = m a.
When a force is perpendicular to the path, α = 90°, cosα = 0, the force performs no work. Examples of such a situation are the centrifugal force on a mass in uniform circular motion and the gravitational force acting on a satellite in a circular orbit. If a body is in uniform (i.e., has constant speed) straight motion and the only force acting on it is perpendicular to its path, then the body will persist in its uniform straight motion (Newton's first law).
When a force F is anti-parallel to the path (α = 180°), it performs negative work W < 0, since cosα = −1, and |F| and |s| are both greater than zero. The negative work done by the force is converted into a decrease of the kinetic energy T,
- W = ΔT < 0
(ΔT < 0 because T decreases, i.e., T1 < T0).
For example, think of an old-fashioned type of cannon that shoots a cannon ball of mass m straight up. The gun powder explosion gives the ball initial kinetic energy T0 = ½ m v02. The gravitational attraction of the earth performs negative work (force downward, motion of the cannon ball upward), until at the highest point the speed v1 and the kinetic energy T1 = ½ m v12 of the ball are zero. The amount of work performed is W = ΔT = 0−T0 = −T0. At the highest point the motion of the cannon ball reverts direction, it starts falling to earth, and from there on the gravitational attraction performs positive work (direction of motion and force are parallel). The kinetic energy increases again until it achieves its original value T0 = ½ m v02 at the point where the cannon ball arrives again at the cannon. The total work done by the gravitation is zero, the work done on the cannon ball going up cancels the work done on the ball going down. (In this example we ignore friction by the air).
When the the force is conservative (non-dissipative), the work is independent of path, and when furthermore the path is a closed curve, the total work is zero (one way the work is positive and the other way the work is equally large in absolute value, but negative).
As the gravitational field is conservative, we just saw an example of a mass (a cannon ball) making a closed path in a conservative force field. The potential energy U of a mass m close to the surface of the earth is equal to U = mgh, where g is the gravitational acceleration and h is the height. Assuming that the cannon is positioned at height h = 0, the cannon ball starts with potential energy zero, U0 = 0. The work W done by the gravitational field on the cannon ball going upward has two effects: it decreases its kinetic energy—as just discussed—and it increases its potential energy, U1 > U0, so that
- W = −ΔU ≡ −(U1 − U0) = U0 − U1 < 0.
At the highest point, h1, the potential energy is maximum U1 = mgh1 (equal to minus the work performed) and the kinetic energy is zero (this is the point where the motion of the cannon ball changes direction, for a small amount of time its speed is zero). The work done by a conservative force converts a decrease in kinetic energy into an increase of potential energy and conversely:
- W = ΔT = −ΔU, so that ΔT + ΔU = 0.
When the cannon ball dropping down is at height h = 0 again, its kinetic energy is maximum (equal to the energy imparted to it by the exploding gun powder) and its potential energy is zero again.
Mathematical formulation
When the force is not constant along the path, or the path is not straight, it is possible to compute the work by infinitesimal calculus. One divides the path in N pieces Δsi, which are small enough to assume that the force is constant and the piece is straight. The (approximate) total work is obtained by summing the work done along the individual small pieces,
To improve the approximation one makes the pieces Δs smaller and smaller, so that their lengths go to zero. The limit is the path integral
where s0 is the tangent vector to the path at r(t0) ≡ r0 and s1 is tangent at the end point r1 of the path.
To show that the work is converted into an increase in kinetic energy, we write for one mass m
where we used F = m a (Newton's second law) and that the acceleration a is the second derivative of r with respect to time. Integrate
where we used that Δs is tangent to the path, i.e.,
and s0 = s(t0) and s1 = s(t1). Hence
To show that work by a conservative force is converted into decrease in potential energy, we use the relation between force and potential, valid for conservative fields
and
Integrate
In summary,
In total, the conservation of mechanical energy follows
Example of mechanical work
- Work to lift a mass m in the gravitational field of the earth. Close to the surface of the earth, the attractive force is constant and equal to the gravitational acceleration g. The work to lift the mass to a height h is,
- When h is positive, and the mass is at rest before and after the lifting (no kinetic energy), the work is completely converted into potential energy.