User:Boris Tsirelson/Sandbox1

For a mathematical theory, correctness means formalizability. "In practice, the mathematician ... is content to bring the exposition to a point where his experience and mathematical flair tell him that translation into formal language would be no more than an exercise of patience (though doubtless a very tedious one)." Reliability of these experience and flair appears to be high but not perfect. Formalization is especially desirable in complicated cases, but feasible only in very simple cases, unless computers help. (Similarly, without computers a programmer is able to debug only very simple programs.)

A proof assistant is a computer program used interactively for developing human-readable reliable mathematical documents in a formal language. (It is not the same as a non-interactive, fully automated theorem prover.)

Nowadays (about 2010) the most successful project of this class combines

• Isabelle, a generic system for implementing logical formalisms;
• Isar (Intelligible SemiAutomated Reasoning), a versatile language environment for structured formal proofs;
• Proof General, a configurable user interface (front-end) for proof assistants;
• HOL (Higher-Order Logic).

This combination is meant below (unless otherwise stated explicitly), and called just Isabelle (rather than Isabelle/Isar/HOL/Proof General).

Top 100 theorems in Isabelle + Formalizing 100 Theorems + Isabelle + Download and installation + Projects + The Isabelle2009-2 Library + IsarMathLib: A library of formalized mathematics for Isabelle/ZF

WP:fold

Example session

First impressions

An existing file, verified before, is used as the source text in this example. Thus, the session is not really interactive. However, this fact is not known to Isabelle. The proof assistant treats the session as interactive, and the text as new.

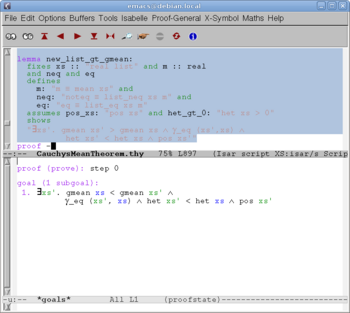
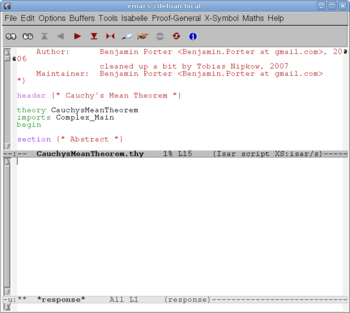
We start Proof General (Fig. 1) and enter the source text (Fig. 2).

(CC) Image: Boris Tsirelson Fig. 1: Proof General welcome (CC) Image: Boris Tsirelson Fig. 2: Source text entered

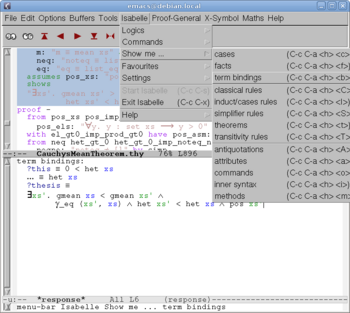
On this stage Proof General does not send the text to Isabelle; we still can edit the text. Proof General helps us by automatic colorization according to the syntax of the Isar language.

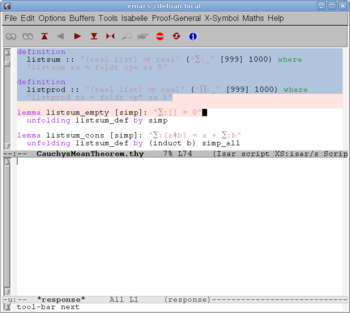
We start a new theory "CauchysMeanTheorem". (The well-know Cauchy's Mean Theorem says that the geometric mean is less than, or equal to, the arithmetic mean, for every finite collection of positive numbers. However, this theorem will appear much later, near the end of the source text.) The existing theory "Complex_Main" is a prerequisite. (It contains main facts about real and complex numbers; only real numbers are relevant, but some useful formulas about $(a+b)^{2}$ appear in "Complex_Main".)

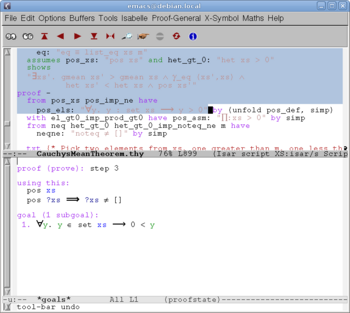
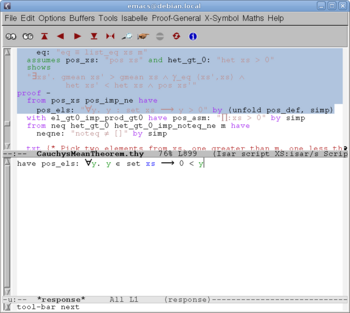
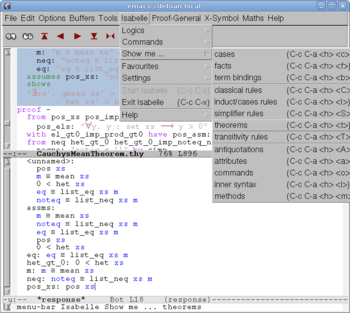
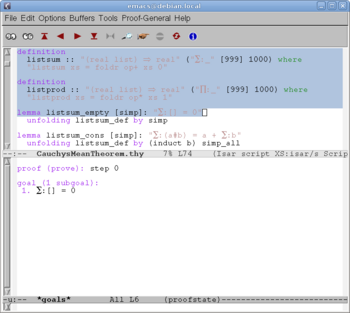
Clicking the red button "$\triangleright$" we send the first portion of the text to Isabelle. After two more such clicks Isabelle reads the line "imports Complex_Main" and finds in the library the "Complex_Main" theory (since it is a prerequisite to the new "CauchysMeanTheorem"), but also "Real", since it appears to be a prerequisite to "Complex_Main", and so on, recursively, until all prerequisites are found and processed (in a logical order). After 9 more clicks we come to the screen shown on Fig. 3. The definitions (and everything before them) are already processed by Isabelle; accordingly, they turn into blue, and become read-only. The formulation of the first lemma is being processed by Isabelle; accordingly, it turns into orange. A fraction of a second later we get Fig. 4. The formulation of the lemma is read by Isabelle; a dialog about its proof starts on the bottom window.

(CC) Image: Boris Tsirelson Fig. 3: Definitions are done; now reading the lemma. (CC) Image: Boris Tsirelson Fig. 4: The proof mode started.

A robot as a student

The first lemma "listsum_empty" (of the new "CauchysMeanTheorem" theory) is ridiculously trivial; it claims that the sum of the empty collection of numbers is equal to zero! Here is an explanation of this disturbing fact.

A human student would not start to learn Cauchy's mean theorem

${\sqrt[{n}]{a_{1}\dots a_{n}}}\leq {\frac {a_{1}+\dots +a_{n}}{n}}$

being unfamiliar with such notions as the sum $(a_{1}+\dots +a_{n})$ and the product $(a_{1}\dots a_{n})$ of n numbers. However, a robot (like Isabelle) is not a human. A robot never was in a kindargarten or elementary school. We cannot say to Isabelle: "Look, here is a sum of three numbers: 15+5+10=30; note that also 5+10+15=30 etc. Likewise, any finite collection of numbers has its sum." Children proceed from the particular to the general, but proof assistants proceed from the general to the particular.

For now, Isabelle is not well-educated. Its mathematical knowledge is rather fragmentary. Some volunteers contribute some theories to the library of Isabelle; this is not a well-organized process rich of resources. Each contributor has to find out, which of the relevant facts are already known to Isabelle and which are not.

Definitions of the sum and the product of a list of numbers are given to Isabelle just before the first lemma (see "listsum" and "listprod" on Fig. 3,4) in terms of

• the sum and the product of two numbers (already known), and
• "foldr", the right fold operation defined in the "List" theory (one of the prerequisites).

Informally, the right fold applies to a binary operation (say, "+"), a list (say, "[x,y,z]") and an initial value (say, "a"), giving "x+(y+(z+a))"; more formally,

foldr op+ [x,y,z] a  =  x+(y+(z+a)).

(For this operation one may write just "x+y+z+a", but in general an operation need not be associative.) The "listsum" definition stipulates the sum operation and the initial value 0; the "listprod" definition stipulates the multiplication operation and the initial value 1. The sum of a list is denoted by Isabelle as follows:

$\Sigma :[x,y,z]=x+(y+(z+0))\,.$

A human student, given by such a formal definition of sum (only sketched here) would not be too disturbed by the trivial exercise "prove that the sum of the empty list is equal to 0"; this is the "listsum_empty" lemma. After the formulation, the source text contains a hint to the proof,

unfolding listsum_def by simp

which means informally: Isabelle, use the definition of the sum of a list, do evident simplifications, and hopefully you'll find a proof of the lemma.

Now we continue the example session.

More

(CC) Image: Boris Tsirelson Fig. 5: ? (CC) Image: Boris Tsirelson Fig. 6: ?

---

(CC) Image: Boris Tsirelson
"We have", why?

(CC) Image: Boris Tsirelson
Here is why!

(CC) Image: Boris Tsirelson
Really complicated arguments...

(CC) Image: Boris Tsirelson
Happy end is coming.

(CC) Image: Boris Tsirelson
The theorem is proved.

(CC) Image: Boris Tsirelson
Some options of the Proof General.

(CC) Image: Boris Tsirelson
Isabelle, show us your methods...

(CC) Image: Boris Tsirelson
...and your term bindings...

(CC) Image: Boris Tsirelson
...and the theorems.

References

Bourbaki, Nicolas (1968), Elements of mathematics: Theory of sets, Hermann (original), Addison-Wesley (translation).