User:Boris Tsirelson/Sandbox1

In Newtonian mechanics, coordinates of moving bodies are functions of time. For example, the classical equation for a falling body; its height h at a time t is

$h=f(t)=h_{0}-0.5gt^{2}$

(here h₀ is the initial height, and g is the acceleration due to gravity). Infinitely many corresponding values of t and h are embraced by a single function f.

PD Image
Vibrating string: a function changes in time

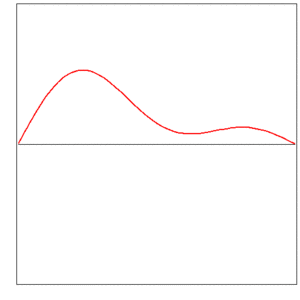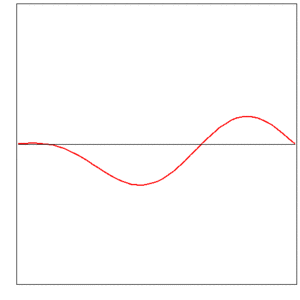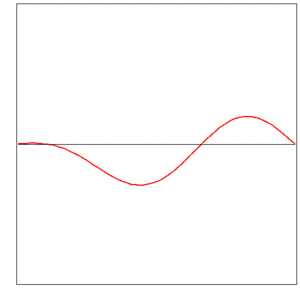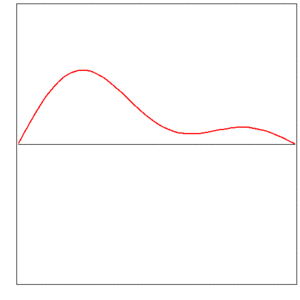
The instantaneous shape of a vibrating string is described by a function (the displacement y as a function of the coordinate x), and this function changes in time:

$y=f_{t}(x).$

Infinitely many functions f_t are embraced by a single function f of two variables,

$y=f(x,t).$

After some speculations by Galileo and mathematical interpretation by Brook Taylor (1715/1717) and Johann Bernoulli (1727), the mathematical theory of vibrating string was started by Jean d'Alembert (1746/1749). His approach is equivalent to a partial differential equation written out by Leonhard Euler in 1755,

${\frac {\partial ^{2}}{\partial t^{2}}}f(x,t)={\frac {\partial ^{2}}{\partial x^{2}}}f(x,t),$

now well-known as the one-dimensional wave equation. D'Alembert found a solution as the superposition of two waves, one traveling to the right, the other to the left:

$f(x,t)=\phi (x+t)+\psi (x-t).$

The initial shape of the string is given by the function f₀. It was a controversial question in the 18th century, whether f₀ must develop into a power series, or not necessarily.

D'Alembert held the opinion that the de-facto standard mentioned above still applies; f₀ must be represented by a single equation. (He changed his opinion in 1780.)

The old standard was repudiated by Euler in 1744. He introduced "mixed" functions, given by different equations on two or more intervals. Moreover, he admitted functions that do not comply with any analytical law, whose graphs are traced by a free stroke of the hand.

Physically, the vibrating string may be thought of as an infinite collection of non-interacting harmonic oscillators (vibratory modes, harmonics). This idea, previously used by Euler in some special cases, turned into a general method of solving the wave equation by Daniel Bernoulli (1755). To this end the initial function has to be developed into a trigonometric series

$f_{0}(x)=c_{1}\sin x+c_{2}\sin 2x+c_{3}\sin 3x+\dots$

It was unclear, how many functions can be so developed. D. Bernoulli believed that a trigonometric series is as general as a power series. Both d'Alembert and Euler believed that a trigonometric series is less general than a power series. The truth was revealed only in the 19th century: in fact, a trigonometric series is more general than a power series!

Heat conduction is physically very different from vibrating string, but mathematically it is again about a function that changes in time, and leads to another partial differential equation

${\frac {\partial }{\partial t}}f(x,t)={\frac {\partial ^{2}}{\partial x^{2}}}f(x,t),$

now well-known as the one-dimensional heat equation. It was first investigated by Joseph Fourier (1807/1822). According to Fourier, the general solution is

$f(x,t)=c_{0}+c_{1}e^{-t}\sin x+c_{2}e^{-4t}\sin 2x+c_{1}e^{-9t}\sin 3x+\dots$