Sine rule: Difference between revisions
imported>Paul Wormer (→Lemma) |
imported>Paul Wormer No edit summary |
||
| Line 18: | Line 18: | ||
[[Image:Proof sine rule2.png|right|thumb|200px|Fig. 3]] | [[Image:Proof sine rule2.png|right|thumb|200px|Fig. 3]] | ||
===Proof of sine rule=== | ===Proof of sine rule=== | ||
| Line 27: | Line 25: | ||
</math> | </math> | ||
where ''d'' is the diameter of the circle. From this result the sine rule follows. | where ''d'' is the diameter of the circle. From this result the sine rule follows. | ||
==External link== | |||
[http://madmath.madslideruling.com/precalculus/sinerule.html Life lecture on Sine Law] | |||
Revision as of 09:12, 18 October 2008
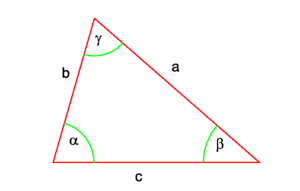
In trigonometry, the sine rule states that the ratio of the sines of the angles of a triangle is equal to the ratio of the lengths of the opposite sides, see Fig.1. Equivalently,
Proof
The easiest proof is purely geometric.
Lemma
In Fig. 2 the angle β satisfies,
Indeed, in Fig. 2 we see two angles, α and β, that share a segment of the circle (have the chord a in common). By a well-known theorem of plane geometry it follows that the angles are equal. The angle α, having the diameter of the circle d as one of its sides, has as opposite angle a right angle. Hence sin(α) = a/d, the length of chord a divided by the diameter d. It follows that the angle β, with a corner on the circumference of the same circle as α, but other than that arbitrary, has the same sine as α.
Proof of sine rule
From the lemma follows that the angles in Fig. 3 are
where d is the diameter of the circle. From this result the sine rule follows.