Tetration

Fig.1. Tetration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{tet}_b(x)} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\mathrm{e}} , $b=2$, $b=\exp(1/\mathrm {e} )$, and $b={\sqrt {2}}$ versus $x$.

This article is currently under construction. While, use article from wikipedia http://en.wikipedia.org/wiki/Tetration

Definiton

For real $b>1$, Tetration $F=\mathrm {tet} _{b}$ on the base $b$ is function of complex variable, which is holomorphic at least in the range $\{z\in \mathbb {C} :~\Re (z)>-2\}$, bounded in the range $\{z\in \mathbb {C} :~|\Re (z)|\leq 1\}$, and satisfies conditions

$F(z+1)=\exp _{b}\!{\big (}F(z){\big )}$

$F(0)=1$

$F\!{\big (}z^{*}{\big )}=F{\big (}z{\big )}^{*}$

at least within range $\Re (z)>-2$.

Real values of the arguments

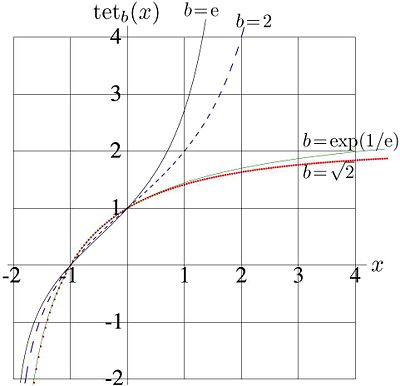
Examples of behavior of this function at the real axis are shown in figure 1 for values $b=\mathrm {e}$, $b=2$, $b=\exp(1/\mathrm {e} )$, and for $b={\sqrt {2}}$. It has logarithmic singularity at $-2$, and it is monotonously increasing function.

At $b\leq \exp(1/\mathrm {e} )$ tetration $\mathrm {tet} _{b}(x)$ approaches its limiting value as $x\rightarrow +\infty$, and $\displaystyle \lim _{x\rightarrow +\infty }~\mathrm {tet} _{b}(x)>1$.

At $b>\exp(1/\mathrm {e} )$ tetration $\mathrm {tet} _{b}(x)$ grows faster than any exponential function. For this reason the tetration is suggested for the representation of huge numbers in mathematics of computation. A number, that cannot be stored as floating point, could be stored as $\mathrm {tet} _{b}(x)$ for some standard value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} (for example, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=2} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\mathrm{e}} ) and relatively moderate value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . The analytic properties of tetration could be used for the implementation of arithmetic operations with huge numbers without to convert them to the floating point representation.

Integer values of the argument

For integer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} , tetration

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm tet}_b}

Etymology

Creation of word tetration is attributed to Englidh mathematician Reuben Louis Goodstein .

Piecewice tetration

uxp

Analytic tetration

This section is not yet written. There is non-finished draft at User:Dmitrii Kouznetsov/Analytic Tetration.

Free online sources

• http://reglos.de/lars/ffx.html , Lars Kindermann. References about Iterative Roots and Fractional Iteration.
• http://math.eretrandre.org/tetrationforum/index.php , Discussion about tetration
• http://tetration.itgo.com/ Tetration site by Andrew Robbins
• http://www.tetration.org/ Tetration site by Daniel Geisler