Ampere's equation: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer |
||
| Line 23: | Line 23: | ||
==Two loops== | ==Two loops== | ||
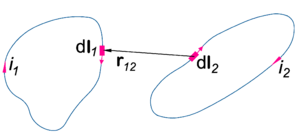
Let <math>\scriptstyle i_1</math> and <math>\scriptstyle i_2</math> be electric currents constant in time. They run in separate loops, see figure on the right, where all quantities are defined. The total force between two loops is given by the double path integral over the loops | Let <math>\scriptstyle i_1</math> and <math>\scriptstyle i_2</math> be electric currents constant in time. They run in separate loops (closed curves) ''C''<sub>1</sub> and ''C''<sub>2</sub>, see figure on the right, where all quantities are defined. The total force between two loops is given by the double path integral over the loops | ||
:<math> | :<math> | ||
\mathbf{F}_{12} = -k i_1 i_2 \oint_{ | \mathbf{F}_{12} = -k i_1 i_2 \oint_{C_1}\oint_{C_2} \frac{ (d\mathbf{l}_1 \cdot d\mathbf{l}_2)\, \mathbf{r}_{12} }{|\mathbf{r}_{12}|^3}. | ||
\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad (1) | |||
</math> | </math> | ||
==Alternative expression== | |||
One can find on the internet the asymmetric (in interchange of the two currents) expression: | |||
:<math> | |||
\mathbf{F}_{12} = k i_1 i_2 \oint_{C_1}\oint_{C_2} \frac{ d\mathbf{l}_1 \times( d\mathbf{l}_2\, \times \mathbf{r}_{12} )}{|\mathbf{r}_{12}|^3}, | |||
\qquad\qquad\qquad\qquad\qquad\qquad\qquad (2) | |||
</math> | |||
instead of the simpler expression in Eq. (1). Here the multiplication signs indicate [[vector products]]. The force in Eq. (2) has in fact two contribution as follows from the result well-known in [[vector analysis]], | |||
:<math> | |||
\frac{ d\mathbf{l}_1 \times( d\mathbf{l}_2\, \times \mathbf{r}_{12} )} {|\mathbf{r}_{12}|^3} = | |||
\frac{( d\mathbf{l}_1 \cdot \mathbf{r}_{12} )\, d\mathbf{l}_2}{|\mathbf{r}_{12}|^3} - \frac{(d\mathbf{l}_1 \cdot d\mathbf{l}_2)\, \mathbf{r}_{12}}{|\mathbf{r}_{12}|^3} . | |||
</math> | |||
The second contribution of Eq. (2) is obviously equal to Eq. (1). We will show that the first contribution vanishes after integration over a closed curve. | |||
Write | |||
:<math> | |||
\frac{\mathbf{r}_{12}}{|\mathbf{r}_{12}|^3} = -\boldsymbol{\nabla}_1 \left(\frac{1}{|\mathbf{r}_{12}|}\right) \equiv -\mathbf{A}, | |||
</math> | |||
where '''A''' is a short hand notation. | |||
Applying [[Stokes' theorem]], we find that the first contribution becomes | |||
:<math> | |||
-k i_1 i_2 \oint_{C_2}\left[ \oint_{C_1} (d\mathbf{l}_1 \cdot \mathbf{A})\,\right] d\mathbf{l}_2 = - k i_1 i_2 \oint_{C_2} \left[\iint_S (\boldsymbol{\nabla}_1 \times \mathbf{A}) \cdot d\mathbf{S}_1 \, \right]d\mathbf{l}_2. | |||
</math> | |||
Again, it is well-known in vector analysis that | |||
:<math> | |||
\boldsymbol{\nabla}_1 \times \boldsymbol{\nabla}_1 \Phi = 0 | |||
</math> | |||
for any scalar function and Φ in particular for Φ ≡ 1/|'''r'''<sub>12</sub>|. Hence the first contribution to the force in Eq. (2) vanishes. | |||
==See also== | ==See also== | ||
*[[Biot-Savart's law]] | *[[Biot-Savart's law]] | ||
Revision as of 12:05, 20 February 2008
In physics, more particularly in electrodynamics, Ampère's equation describes the force between two infinitesimal elements of electric-current-carrying wires. The equation is named for the early nineteenth century French physicist and mathematician André-Marie Ampère.
Rather than giving the infinitesimal equation, which is not without problems,[1][2] we will describe two common cases obtained by integration: a system consisting of two straight wires and a system of two closed loops. Since the integrals over disputed terms in Ampère's infinitesimal equation vanish, the equations for these integrated systems are generally accepted and, moreover, are in full agreement with experiment.
Electromagnetic units
Equations[3] will be given in two common systems of electromagnetic units (SI and Gaussian) and to that end we define the constant k as follows,
Here μ0 is the magnetic constant (also known as vacuum permeability). The quantity c is the velocity of light in the vacuum 299 792 458 m s−1 exactly) .
Two straight, infinite, and parallel wires
Consider two wires, one carrying an electric current , the other . Both currents are constant in time; the wires are infinite, straight, and parallel. If the wires are a distance r apart, the force (per length l of wire) between them is,
The force is attractive if the currents run in the same direction and repulsive if they flow in opposite direction. This equation is used to define the SI unit of current A (ampere). Take wires in vacuum, r = 1 m, l = 1 m, F = 2 ⋅ 10−7 N , and equal currents, then the currents are equal to 1 A. Note that in SI units this implies that μ0 = 4π ⋅ 10−7 N/A2.
.
Two loops
Let and be electric currents constant in time. They run in separate loops (closed curves) C1 and C2, see figure on the right, where all quantities are defined. The total force between two loops is given by the double path integral over the loops
Alternative expression
One can find on the internet the asymmetric (in interchange of the two currents) expression:
instead of the simpler expression in Eq. (1). Here the multiplication signs indicate vector products. The force in Eq. (2) has in fact two contribution as follows from the result well-known in vector analysis,
The second contribution of Eq. (2) is obviously equal to Eq. (1). We will show that the first contribution vanishes after integration over a closed curve.
Write
where A is a short hand notation. Applying Stokes' theorem, we find that the first contribution becomes
Again, it is well-known in vector analysis that
for any scalar function and Φ in particular for Φ ≡ 1/|r12|. Hence the first contribution to the force in Eq. (2) vanishes.
See also
References
- ↑ E. Whittaker, A History of the Theories of Aether and Electricity, vol. I, 2nd edition, Nelson, London (1951). Reprinted by the American Institute of Physics, (1987). pp. 85-88
- ↑ C. Christodoulides, Comparison of the Ampère and Biot-Savart magnetostatic force laws in their line-current-element forms, American Journal of Physics, vol. 56, pp. 357-362 (1988)
- ↑ J. D. Jackson, Classical Electrodynamics, 2nd edition, John Wiley, New York (1975) pp. 172-173








![{\displaystyle -ki_{1}i_{2}\oint _{C_{2}}\left[\oint _{C_{1}}(d\mathbf {l} _{1}\cdot \mathbf {A} )\,\right]d\mathbf {l} _{2}=-ki_{1}i_{2}\oint _{C_{2}}\left[\iint _{S}({\boldsymbol {\nabla }}_{1}\times \mathbf {A} )\cdot d\mathbf {S} _{1}\,\right]d\mathbf {l} _{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/210e07091d4d3214c501672a52b080cb4f95ba10)
