Polar coordinates

Two dimensional polar coordinates r and θ of vector $\scriptstyle {\vec {\mathbf {r} }}$

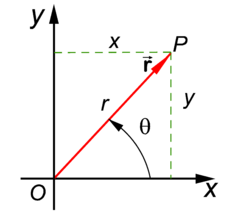
In mathematics and physics, polar coordinates give the position of a vector $\scriptstyle {\vec {\mathbf {r} }}$ in two-dimensional real space $\scriptstyle \mathbb {R} ^{2}$. A Cartesian system of two orthogonal axes is presupposed. One number (r) gives the length of the vector and the other number (θ) gives the angle of the vector with the x-axis of the Cartesian system (measured in the direction of the positive y-axis).

Definition

The polar coordinates are related to the Cartesian coordinates x and y through

${\begin{aligned}r&={\sqrt {x^{2}+y^{2}}}\\x&=r\cos \theta \\y&=r\sin \theta ,\\\end{aligned}}$

so that for r ≠ 0,

$\theta ={\begin{cases}\arccos(x/r)&{\hbox{ if }}y\geq 0\\360^{0}-\arccos(x/r)&{\hbox{ if }}y<0.\\\end{cases}}$

Surface element

The infinitesimal surface element in polar coordinates is

$dA=J\,dr\,d\theta .$

The Jacobian J is the determinant

$J={\frac {\partial (x,y)}{\partial (r,\theta )}}={\begin{vmatrix}\cos \theta &-r\sin \theta \\\sin \theta &r\cos \theta \\\end{vmatrix}}=r.$

Example: the area A of a circle of radius R is given by

$A=\int _{0}^{2\pi }\int _{0}^{R}r\,dr\,d\theta =\pi R^{2}$