User:Aleksander Stos/ComplexNumberAdvanced: Difference between revisions
imported>Aleksander Stos m (preliminary formatting) |
imported>Aleksander Stos (expo) |
||
| Line 31: | Line 31: | ||
Obviously, the conjugation is just the symmetry with respect to the x-axis. | Obviously, the conjugation is just the symmetry with respect to the x-axis. | ||
;Trigonometric form | ;Trigonometric and exponential form | ||
As the graphical representation suggests, any complex number ''z=a+bi'' of modulus 1 (i.e. a point from the unit circle) can be written as <math>z=\cos \theta + i\sin\theta</math> | As the graphical representation suggests, any complex number ''z=a+bi'' of modulus 1 (i.e. a point from the unit circle) can be written as <math>z=\cos \theta + i\sin\theta</math> | ||
for some <math>\theta\in [0,2\pi).</math> So actually any (non-null) <math>z\in\mathbb{C}</math> can be represented as | for some <math>\theta\in [0,2\pi).</math> So actually any (non-null) <math>z\in\mathbb{C}</math> can be represented as | ||
| Line 37: | Line 37: | ||
This is the ''trigonometric form'' of the complex number ''z''. If we adopt convention that <math>\theta \in [0,2\pi)</math> then such <math>\theta</math> is unique and called the ''argument'' of ''z''.<ref>In literature the convention <math>\theta\in (-\pi,\pi]</math> is found as well.</ref> | This is the ''trigonometric form'' of the complex number ''z''. If we adopt convention that <math>\theta \in [0,2\pi)</math> then such <math>\theta</math> is unique and called the ''argument'' of ''z''.<ref>In literature the convention <math>\theta\in (-\pi,\pi]</math> is found as well.</ref> | ||
Graphically, the number <math>\theta</math> is the (oriented) angle between the ''x''-axis and the interval containing 0 and ''z''. | Graphically, the number <math>\theta</math> is the (oriented) angle between the ''x''-axis and the interval containing 0 and ''z''. | ||
Closely related is the exponential notation. | |||
If we define complex exponential as | |||
:<math>e^z = \sum_0^\infty \frac{z^n}{n!},</math> | |||
then it may be shown that | |||
:<math>e^{i\theta}=\cos\theta + i\sin\theta,\quad\quad \theta\in\mathbb{R}. </math> | |||
Consequently, any (non-zero) <math> z\in \mathbb{C}</math> can be written as | |||
:<math> z= r e^{i\theta}</math> with the same ''r'' and ''theta'' as above. | |||
This is called the ''exponential form'' of the complex number ''z''. | |||
The trigonometric form is particularly well adapted to perform multiplication. If <math>z_1=r_1(\sin( | |||
Revision as of 07:36, 13 August 2007
This is an experimental draft. For a brief description of the project and motivations click here.
Complex numbers are defined as ordered pairs of reals:
Such pairs can be added and multiplied as follows
- addition:
- multiplication:
with the addition and multiplication is the field of complex numbers. From another of view, with complex additions and multiplication by real numbers is a 2-dimesional vector space.
To perform basic computations it is convenient to introduce the imaginary unit, i=(0,1).[1] It has the property Any complex number can be written as (this is often called the algebraic form) and vice-versa. The numbers a and b are called the real part and the imaginary part of z, respectively. We denote and Notice that i makes the multiplication quite natural:
The square root of number in the denominator in the above formula is called the modulus of z and denoted by ,
We have for any two complex numbers and
- provided
For we define also , the conjugate, by Then we have
- provided
- Geometric interpretation
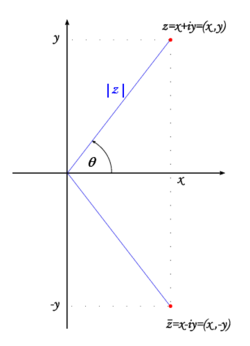
Complex numbers may be naturally represented on the complex plane, where corresponds to the point (x,y), see the fig. 1.
Obviously, the conjugation is just the symmetry with respect to the x-axis.
- Trigonometric and exponential form
As the graphical representation suggests, any complex number z=a+bi of modulus 1 (i.e. a point from the unit circle) can be written as for some So actually any (non-null) can be represented as
- where r traditionally stands for |z|.
This is the trigonometric form of the complex number z. If we adopt convention that then such is unique and called the argument of z.[2] Graphically, the number is the (oriented) angle between the x-axis and the interval containing 0 and z. Closely related is the exponential notation. If we define complex exponential as
then it may be shown that
Consequently, any (non-zero) can be written as
- with the same r and theta as above.
This is called the exponential form of the complex number z.
The trigonometric form is particularly well adapted to perform multiplication. If <math>z_1=r_1(\sin(



































![{\displaystyle \theta \in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2742d923047f035ec3e8db8259485fda0629104b)