Lambert W function: Difference between revisions
imported>Fredrik Johansson No edit summary |
imported>Fredrik Johansson |
||
| Line 10: | Line 10: | ||
[[Image:Lambertw.png|400px|center|]] | [[Image:Lambertw.png|400px|center|]] | ||
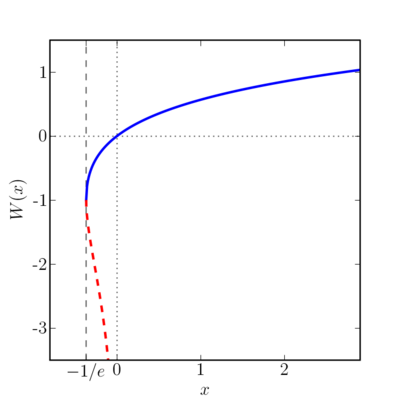
The function has two real branches in the interval <math>-1/e < x < 0</math>. Concretely, this means that the equation <math>x = w e^w</math> has two real solutions if <math>x</math> lies in that interval. For example, if <math>x = -0.15</math> (which is about half way between <math>-1/e</math> and 0), there is one solution <math>\scriptstyle w_0 \approx -0.17</math> that lies on the blue graph and another solution <math>\scriptstyle w_1 \approx -3.0</math> that lies on the dashed red graph. | |||
==History and application== | ==History and application== | ||
Revision as of 15:44, 26 April 2007
The Lambert W function is used in mathematics to solve equations in which the unknown appears both as a linear term and in the argument of an exponential function or a logarithm, such as or . Such equations cannot otherwise, except in special cases, be solved explicitly in terms of algebraic operations, exponentials and logarithms.
Definition
The Lambert W function is defined as the multivalued function that satisfies
for any complex number . Equivalently, it may be defined as the inverse function of . An equation can be solved by rewriting it in the canonical form , after which the solution is given by . The multivaluedness of the Lambert W function means that the equations it may be used to solve generally have more than one solution.
The function has two real branches in the interval . Concretely, this means that the equation has two real solutions if lies in that interval. For example, if (which is about half way between and 0), there is one solution that lies on the blue graph and another solution that lies on the dashed red graph.
History and application
Equations of the kind that can be solved analytically with the Lambert W function are common in mathematics and science, yet the utility of such a function was not realized until recently. The Lambert W function was introduced in the 1980's as a function in the Maple computer algebra system, whose interface required an explicit notation for solutions of equations. The function's history highlights the importance of good mathematical notation: due to previously not being recognized as a function in its own right, it had not been studied systematically, despite its most important properties requiring only elementary complex analysis. An account of the function and its history that helped popularize it is given in a 1996 paper by R. M. Corless et al. (with Donald Knuth a notable co-author).[1]
The basic theory behind the Lambert W function was investigated in 1779 by Leonhard Euler.[2] The Maple developers chose the name of Johann Heinrich Lambert instead of Euler's since Euler had referenced work by Lambert in his paper, and possibly because "naming yet another function after Euler would not be useful".[3]
Since its introduction, the Lambert W function has been applied to problems ranging from quantum physics to the complexity of algorithms. Cranmer[4] discusses the application of the Lambert W function in solar wind physics and writes in the conclusion: "The Lambert W function used in these solutions was defined and publicized only about a decade ago, but it has rapidly become a convenient tool for mathematical physicists. The elegance of explicit solutions to equations thought previously to be expressible only implicitly is clear, but there also are many practical benefits to having explicit solutions as well."
Mathematical details
To write:
- Taylor series
- Differential equation
- Integral
- Asymptotics
- Calculation
Particular values of the Lambert W function include and . The value
has been named the omega constant. Eric Weisstein notes that, as it satisfies , it "can be considered a sort of 'golden ratio' of exponentials".[5]
See also
References
- ↑ R. M. Corless, R. M., Gonnet, G. H., Hare, D. E. G., Jeffrey, D. J. & Knuth, D. E. (1996). "On the Lambert W function". Adv. Computational Maths. 5, 329–359
- ↑ Euler, L. (1779). "De serie Lambertina plurimisque eius insignibus proprietatibus". Originally published in Acta Academiae Scientarum Imperialis Petropolitinae 1779, 1783, pp. 29–51. Also in Opera Omnia: Series 1, Volume 6, pp. 350 - 369. See E532 in The Euler Archive for a scanned copy.
- ↑ Corless, R., Jeffrey, D. & Knuth, D. E. (1997). "A Sequence of Series for the Lambert W Function", ISSAC: Proceedings of the ACM SIGSAM International Symposium on Symbolic and Algebraic Computation (formerly SYMSAM, SYMSAC, EUROSAM, EUROCAL) (also sometimes in cooperation with the Symbolic and Algebraic Manipulation Groupe in Europe (SAME))
- ↑ Cranmer, S. R. (2004). "New views of the solar wind with the Lambert W function". Am. J. Phys. 72, 1397
- ↑ Weisstein, E. W. (April 18, 2005). "Lambert W-Function", MathWorld