Prime number/Citable Version

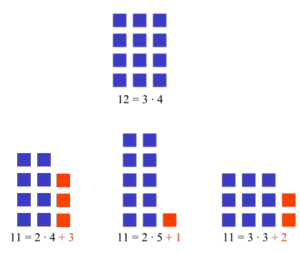
Prime numbers illustrated with square tiles: 12 squares can be arranged into a rectangle with sides of length 3 and 4, so 12 is not a prime number. There is no way to form a full rectangle more than one square wide with 11 squares, so 11 is a prime number.

A prime number is a whole number (i.e., one having no fractional or decimal part) that cannot be evenly divided by any numbers but 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and 17. With the exception of $2$, all prime numbers are odd numbers, but not every odd number is prime. For example, $9=3\cdot 3$ and $15=3\cdot 5$, so neither 9 nor 15 is prime. The study of prime numbers has a long history, going back to ancient times, and it remains an active part of number theory (a branch of mathematics) today. It is commonly believed that the study of prime numbers is an interesting, but not terribly useful, area of mathematical research. While this used to be the case, the theory of prime numbers has important applications now. Understanding properties of prime numbers and their generalizations is essential to modern cryptography, and to public key ciphers that are crucial to Internet commerce, wireless networks and, of course, military applications. Less well known is that other computer algorithms also depend on properties of prime numbers.

Definition

Prime numbers are usually defined to be positive integers (other than 1) with the property that they are only (evenly) divisible by 1 and themselves. In other words, a number $n\in \mathbb {N}$ is said to be prime if there are exactly two $m\in \mathbb {N}$ such that $m|n$, namely $m=1$ and $m=n$.

There is another way of defining prime numbers, and that is that a number is prime if whenever it divides the product of two numbers, it must divide one of those numbers. A nonexample (if you will) is that 4 divides 12, but 4 does not divide 2 and 4 does not divide 6 even though 12 is 2 times 6. This means that 4 is not a prime number. We may express this second possible definition in symbols (a phrase commonly used to mean "in mathematical notation") as follows: A number $p\in \mathbb {N}$ is prime if for any $a,b\in \mathbb {N}$ such that $p|ab$ (read p divides ab), either $p|a$ or $p|b$. If the first characterization of prime numbers is taken as the definition, the second is derived from it as a theorem, and vice versa.

Aside on mathematical notation: The second sentence above is a translation of the first into mathematical notation. It may seem difficult at first (perhaps even a form of obfuscation!), but mathematics relies on precise reasoning, and mathematical notation has proved to be a valuable, if not indispensible, aid to the study of mathematics. It is commonly noted while ancient Greek mathematicians had a good understanding of prime numbers, and indeed Euclid was able to show that there are infinitely many prime numbers, the study of prime numbers (and algebra in general) was hampered by the lack of a good notation, and this is one reason ancient Greek mathematics (or mathematicians) excelled in geometry, making comparatively less progress in algebra and number theory.

Unique factorization

Every integer N > 1 can be written in a unique way as a product of prime factors, up to reordering. to see why this is true, assume that N can be written as a product of prime factors in two ways

$N=p_{1}p_{2}\cdots p_{m}=q_{1}q_{2}\cdots q_{n}$

We may now use a technique known as mathematical induction to show that the two prime decompositions are really the same.

Consider the prime factor $p_{1}$. We know that

$p_{1}\mid q_{1}q_{2}\cdots q_{n}.$

Using the second definition of prime numbers, it follows that $p_{1}$ divides one of the q-factors, say $q_{i}$. Using the first definition, $p_{1}$ is in fact equal to $q_{i}$

Now, if we set $N_{1}=N/p_{1}$, we may write

$N_{1}=p_{2}p_{3}\cdots p_{m}$

and

$N_{1}=q_{1}q_{2}\cdots {\hat {q}}_{i}\cdots q_{n}$

where the circumflex ("hat symbol") indicates that $q_{i}$ is not part of the prime factorization of $N_{1}$.

Continuing this way, we obtain a sequence of numbers $N=N_{0}>N_{1}>N_{2}>\ldots >N_{n}=1$ where each $N_{\alpha }$ is obtained by dividing $N_{\alpha -1}$ by a prime factor. In particular, we see that $m=n$ and that there is some permutation ("rearrangement") σ of the indices $1,2,\ldots n$ such that $p_{i}=q_{\sigma (i)}$. Said differently, the two factorizations of N must be the same up to a possible rearrangement of terms.

There are infinitely many primes

One basic fact about the prime numbers is that there are infinitely man of them. In other words, the list of prime numbers 2, 3, 5, 7, 11, 13, 17, ... doesn't ever stop. There are a number of ways of showing that this is so, but one of the oldest and most familiar proofs goes back go Euclid.

Euclid's proof

Suppose the set of prime numbers is finite, say $\{p_{1},p_{2},p_{3},\ldots ,p_{n}\}$, and let

$N=p_{1}p_{2}\cdots p_{n}+1$

then for each $i\in 1,\ldots ,n$ we know that $p_{i}\not |N$ (because the remainder is 1). This means that N is not divisible by an prime, which is impossible. This contradiction shows that our assumption that there must only be a finite number of primes must have been wrong and thus proves the theorem.

Euler's proof

The Swiss mathematician Leonhard Euler showed how the existence of infinitely many primes could be demostrated using a rather different approach. The starting point is the fact that the harmonic series

$1+{\frac {1}{2}}+{\frac {1}{3}}+\ldots +{\frac {1}{n}}+\ldots$

diverges. That is, for any $N>0$, we can choose n such that

$1+{\frac {1}{2}}+{\frac {1}{3}}+\ldots +{\frac {1}{n}}>N$

A second fact we will need about infinite series is that if $|x|<1$

$1+{\frac {1}{x}}+{\frac {1}{x^{2}}}+\ldots ={\frac {1}{1-x}}$

Now, unique factorization gives us

$\sum _{i=1}^{\infty }{\frac {1}{i}}=\prod _{p}{\frac {1}{1-p}}$

where the sum on the left is the harmonic series, and the product on the right is extended over all primes p. Now, if there are only finitely many primes, the product on the right has a (finite) value, but the harmonic series (the sum on the left) diverges. This shows that there must be infinitely many primes, after all.

Remark: One might well wonder what point there is in offering multiple proofs of the same result. After all, isn't one enough? In mathematics, the point of writing a proof is not so much to establish that something is true, but to understand why it is true. Euclid's proof is purely algebraic, and ultimately depends on the fact that prime numbers can be characterized in two different ways. Euler's proof, on the other hand, makes use of a couple of facts about infinite series combined with the unique factorization property establishe above. What is interesting is that these two proofs (and there are many others) use ideas from very different parts of mathematics to arrive at the same result. One has the feeling that this is evidence of particularly deep interconnections between different parts of mathematics.

Locating primes

How can we tell which numbers are prime and which are not? It is sometimes possible to tell that a number is not prime from looking at its digits: for example, any number larger than 2 whose last digit is even is divisble by 2 and hence not prime, and any number ending with 5 is divisible by 5. Therefore, any prime number larger than 5 must end with 1, 3, 7 or 9. This check can be used to rule out the possibility of a randomly chosen number being prime roughly half of the time, but a number that ends with 1, 3, 7 or 9 could have a divisor that is harder to spot.

To find prime numbers, we must use a systematic procedure — an algorithm. Nowadays, prime-finding calculations are performed by computers, often using very complicated algorithms, but there are simple algorithms that can be carried out by hand if the numbers are small. In fact, the simplest methods for locating prime numbers are some of the oldest algorithms, known since antiquity. Two classical algorithms are called trial division and the sieve of Eratosthenes.

Trial division

Trial division consists of systematically searching the list of numbers 2, 3, ..., $n-1$ for a divisor; if none is found, the number is prime. If n has a small divisor, we can quit as soon as we've found it, but in the worst case — if n is prime — we have to test all $n-2$ numbers to be sure. This algorithm can be improved by realizing the following: if n has a divisor a that is larger than ${\sqrt {n}}$, there must be another divisor b that is smaller than ${\sqrt {n}}$. Thus, it is sufficient to look for a divisor up to ${\sqrt {n}}$. This makes a significant difference: for example, we only need to try dividing by 2, 3, ..., 31 to verify that 997 is prime, rather than all the numbers 2, 3, ..., 996. Trial division might be described as follows using pseudocode:

Algorithm: trial division

Given n,

For each i = 2, 3, ... less than or equal to ${\sqrt {n}}$:

If i divides n:

Return "n is not prime"

Else:

Continue with the next i

When all i have been checked:

Return "n is prime"