Riemann-Hurwitz formula: Difference between revisions
Jump to navigation
Jump to search
imported>William Hart mNo edit summary |
imported>David Lehavi (added picture of pullback triangulation) |
||
| Line 3: | Line 3: | ||
<math>2 (\mbox{genus}(C)-1)=2d(\mbox{genus}(D)-1)+B</math>. | <math>2 (\mbox{genus}(C)-1)=2d(\mbox{genus}(D)-1)+B</math>. | ||
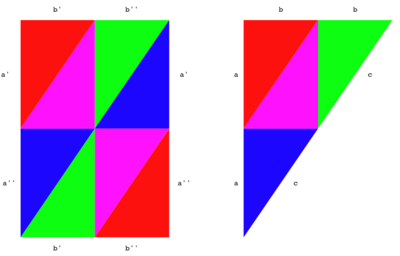
Over a [[field]] in general [[characteristic]], this theorem is a consequence of the [[Riemann-Roch theorem]]. Over the [[complex numbers]], the theorem can be proved by choosing a [[triangulation]] of the curve <math>D</math> such that all the branch points of the map are nodes of the triangulation. One then considers the [[pullback]] of the triangulation to the curve <math>C</math> and computes the [[Euler characteristics]] of both curves. | [[Image:Gludiag.png|400px|thumb|a triangulated gluing diagram for the Riemann sphere, and it's pullback to a torus double cover, which is ramified over the vertices of the triangulation]]Over a [[field]] in general [[characteristic]], this theorem is a consequence of the [[Riemann-Roch theorem]]. Over the [[complex numbers]], the theorem can be proved by choosing a [[triangulation]] of the curve <math>D</math> such that all the branch points of the map are nodes of the triangulation. One then considers the [[pullback]] of the triangulation to the curve <math>C</math> and computes the [[Euler characteristics]] of both curves. | ||
[[Category:Mathematics Workgroup]] | [[Category:Mathematics Workgroup]] | ||
[[Category:CZ Live]] | [[Category:CZ Live]] | ||
Revision as of 13:47, 23 February 2007
In algebraic geometry the Riemann-Hurwitz formula states that if C,D are smooth algebraic curves, and is a finite map of degree then the number of branch points of , denoted by , is given by
.
Over a field in general characteristic, this theorem is a consequence of the Riemann-Roch theorem. Over the complex numbers, the theorem can be proved by choosing a triangulation of the curve such that all the branch points of the map are nodes of the triangulation. One then considers the pullback of the triangulation to the curve and computes the Euler characteristics of both curves.