ArcSin: Difference between revisions
imported>Dmitrii Kouznetsov (→Expansion in vicinity of the branchpoints: remove "math") |
imported>Dmitrii Kouznetsov m (→Real values) |
||
| Line 22: | Line 22: | ||
==Real values== | ==Real values== | ||
[[File:AsinplotT.png|right|300px]] | [[File:AsinplotT.png|right|300px]] | ||
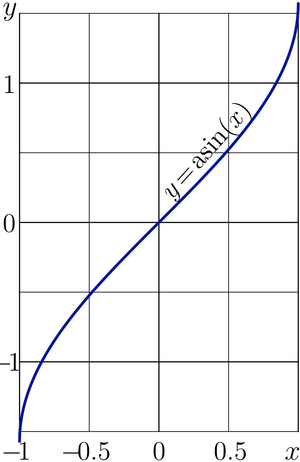
While <math>-1\le x\le 1</math>, id est, along the real axis, <math>\arcsin(x)</math> has real values. The graphic is plotted | While <math>-1\le x\le 1</math>, id est, along the real axis, <math>\arcsin(x)</math> has real values. The graphic is plotted in figure at right. | ||
==Numerical Implementation of ArcSin== | ==Numerical Implementation of ArcSin== | ||
Revision as of 02:34, 2 April 2012
ArcSin, or asign, or arcsin is holomorphic function, inverse of sin.
ArcSin is considered as elementary function
is holomorphic solution of equation
such that
Range of holomorphism
is holomorphic in the whole complex plane except the halflines and .
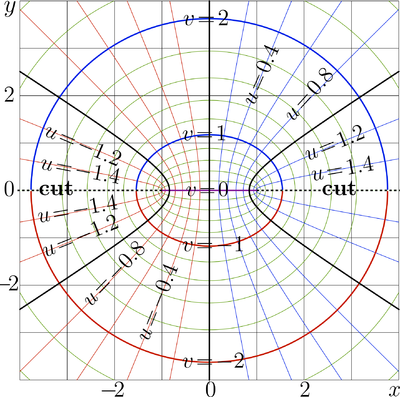
Complex map or </math>f=\arcsin(x+\mathrm i y)</math> is shown in figure at right in the , plane with levels and levels . Thick lines correspond to the Integer values. The cut lines are shown with dashed lines. In vicinity of the cut lines, the real part of ArcSin approach values .
Real values
While , id est, along the real axis, has real values. The graphic is plotted in figure at right.
Numerical Implementation of ArcSin
In some programing languages, acos is implemented only for real argument. However, it can be expressed through the log function as follows:
complex double asin(complex double z){
if(Im(z)<0){if(Re(z)>=0){return M_PI/2.-I*log( z + sqrt(z*z-1.) );}
else{return M_PI/2.-I*log( z - sqrt(z*z-1.) );}}
if(Re(z)>=0){return M_PI/2.+I*log( z + sqrt(z*z-1.) );}
else {return M_PI/2.+I*log( z - sqrt(z*z-1.) );} }
where I denotes the imaginary unity; Re and Im denote the real and imaginary parts; M_PI denotes $\pi$.
Fortunately, in the C++ compilers, function log is already implemented for complex double argument.
This implementation above used to plot the complex map of ArcSin at the top figure. In particular, the same representation can be used for real values of the argument; the explicit plot of ArcSin is generated with the same representation. (Click the figure to see the code used for its generation.) However, the last graphic could be generated also with the internal C++ function asin of real argument, as well as with flipping of plot of function sin.
Expansions
Expansion at zero
Often, the expansions of Sin and ArcSin at small values of argument are used;
Mathematica allows to evaluate many terms of this expantion:
arcsin(z) = z + 0.166666666666667
z3 + 0.0750000000000000
z5 + 0.0446428571428571
z7 + 0.0303819444444444
z9 + 0.0223721590909091
z11 + 0.0173527644230769
z13 + 0.0139648437500000
z15 + 0.0115518008961397
z17 + 0.00976160952919408
z19 + 0.00839033580961682
z21 + 0.00731252587359885
z23 + 0.00644721031188965
z25 + ..
Expansion in vicinity of the branchpoints
Extremums of function Sin correspond to branch points of ArcSin. The expansions can be written as follows:
Mathematica allows to evaluate many of terms of this expansion;
arcsin(-1+t) =- 1.5707963267948966 + 1.4142135623730950 $ $ +0.117851130 19775792 t +0.026516504294495532 t2+0.0078918167543141465 t3 + 0.0026854098677874526 t4+ 0.00098871908768538028 t5+ 0.00038344554362157376 t6+ 0.00015429118302868087 t7+ 0.000063815287098259552 t8+ 0.000026962891771048261 t9+ 0.000011587623725414788 t10 +0.0000050495474929920175 t11 +0.0000022260088531606476 t12 +...
Similar expansion of ArcSin can be written at another branch point:
The expansions above allow to evaluate ArcSin at least in vicinity of the segment ; the precision of evaluation can be improved with the iteration
References
Some part of the content above is copypasted from TORI, http://tori.ils.uec.ac.jp/TORI/index.php/ArcSin






















![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

