Centrifugal force: Difference between revisions
imported>John R. Brews m (→Whirling table: promote header) |
imported>John R. Brews (→Rotating spheres: reword to fit modified figure) |
||
| Line 12: | Line 12: | ||
==Rotating spheres== | ==Rotating spheres== | ||
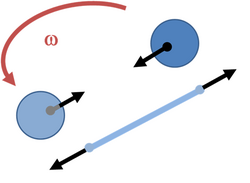
{{Image|Rotating-sphere forces.PNG|right|250px| Exploded view of rotating spheres in an inertial frame of reference showing the centripetal forces on the spheres provided by the tension in a rope tying them together.}} | {{Image|Rotating-sphere forces.PNG|right|250px| Exploded view of rotating spheres in an inertial frame of reference showing the centripetal forces on the spheres provided by the tension in a rope tying them together.}} | ||
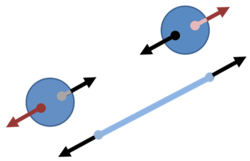
{{Image|Rotating spheres in rotating frame.PNG|right|250px|Rotating spheres subject to centrifugal force in a co-rotating frame.}} | {{Image|Rotating spheres in rotating frame.PNG|right|250px|Rotating spheres subject to centrifugal (outward) force in a co-rotating frame in addition to the (inward) tension from the rope.}} | ||
Consider two identical balls isolated in space, but connected by a rope. We ignore any effects of gravity. We observe the tension in the rope, for example, by placing a spring in the center of the rope and measuring its stretch when the rope is under tension. We sit at the center of the rope and inquire whether the two balls are rotating about us. | Consider two identical balls isolated in space, but connected by a rope. We ignore any effects of gravity. We observe the tension in the rope, for example, by placing a spring in the center of the rope and measuring its stretch when the rope is under tension. We sit at the center of the rope and inquire whether the two balls are rotating about us. | ||
| Line 21: | Line 21: | ||
Let us now look at this tension from the viewpoint of the inertial observers: they see the balls rotating with an angular rate of (say) ω radians/s. That means the balls have a speed of ''v = ωR'' where 2''R'' is the separation of the centers of the balls. Their circular motion means that each ball is subject to an inward [[centripetal force]] provided by the tension in the rope, of magnitude ''F<sub>T</sub> = mv<sup>2</sup>/R = mRω<sup>2</sup>'', and the measured stretch of the spring reflects exactly this force. | Let us now look at this tension from the viewpoint of the inertial observers: they see the balls rotating with an angular rate of (say) ω radians/s. That means the balls have a speed of ''v = ωR'' where 2''R'' is the separation of the centers of the balls. Their circular motion means that each ball is subject to an inward [[centripetal force]] provided by the tension in the rope, of magnitude ''F<sub>T</sub> = mv<sup>2</sup>/R = mRω<sup>2</sup>'', and the measured stretch of the spring reflects exactly this force. | ||
Next, let's look at things from the viewpoint of the rotating observers sitting at the center of the rope. They see the balls as stationary, because they are rotating with them. Because they rotate at the same rate as the spheres, they are said to be in a ''co-rotating frame''. But they also see the stretched spring. | Next, let's look at things from the viewpoint of the rotating observers sitting at the center of the rope. They see the balls as stationary, because they are rotating with them. Because they rotate at the same rate as the spheres, they are said to be in a ''co-rotating frame''. But they also see the stretched spring. Despite the tension from the stretched string, the balls do not move, so they are subject to no net force. The rotating observers succeed in using Newton's laws to explain the tension despite no motion, and to explain no motion despite the tension because, in their rotating frame, they experience a ''centrifugal force'', an outward force radiating from their center position that affects all bodies they observe (including themselves if they move off-center). This centrifugal radially outward force on objects at distance ''R'' is of magnitude ''mRω<sup>2</sup>'', but of course, these rotating observers simply see that this is the tension in the spring, and they cannot ''calculate'' its magnitude from scratch because they cannot measure the rotational rate ''ω''. | ||
However, if they are quite sophisticated, the rotating observers will notice that the centrifugal force they observe on every object they measure has some peculiar properties not shared by forces like gravity, or electrical forces. In particular, it has no observable source in a mass or a charge, like other physical forces, and appears to become larger the further you go from its radiating center, instead of weakening with distance like other forces. So they might conclude that this is an inertial force and try to explain their observations based upon their frame seen as a rotating frame, and calculate their rate of rotation using the measured tension and the formula ''F<sub>T</sub> = mRω<sup>2</sup>''. If they did that, then their calculations would be mapped into an inertial frame, and they would analyze the situation the same way as an inertial observer. They then would use centripetal force instead of centrifugal force in their calculations, but as they move about in their rotating frame, their immediate visceral experience of the centrifugal force will be a real part of their everyday experience. | However, if they are quite sophisticated, the rotating observers will notice that the centrifugal force they observe on every object they measure has some peculiar properties not shared by forces like gravity, or electrical forces. In particular, it has no observable source in a mass or a charge, like other physical forces, and appears to become larger the further you go from its radiating center, instead of weakening with distance like other forces. So they might conclude that this is an inertial force and try to explain their observations based upon their frame seen as a rotating frame, and calculate their rate of rotation using the measured tension and the formula ''F<sub>T</sub> = mRω<sup>2</sup>''. If they did that, then their calculations would be mapped into an inertial frame, and they would analyze the situation the same way as an inertial observer. They then would use centripetal force instead of centrifugal force in their calculations, but as they move about in their rotating frame, their immediate visceral experience of the centrifugal force will be a real part of their everyday experience. | ||
Revision as of 15:01, 15 February 2011
Centrifugal force (from Latin centrum "center" and fugere "to flee") refers to an outward force experienced by a body on a curved path that is directed away from the center of curvature. Such a force is experienced in a reference frame attached to the body, which (because the body is not in a uniform straight-line motion) is an accelerating reference frame, not an inertial reference frame. Such a body also may experience other forces due to its acceleration, namely the Coriolis force and the Euler force.
Reference frames
Newton's laws of motion are expressed for observations made in an inertial frame of reference, commonly referred to as any frame of reference that is in straight-line motion at constant speed relative to the "fixed stars", an historical reference taken today to refer to the entire universe. However, everyday experience does not take place in such a reference frame. For example, we live upon planet Earth, which rotates about its axis (an accelerated motion), orbits the Sun (another accelerated motion), and moves with the Milky Way (still another accelerated motion). These motions are slight, although they do affect matters such as aiming artillery pieces and plotting transoceanic air flights. More visceral examples of everyday experience of non-inertial frames are roller coaster rides and simply turning a sharp corner in a car. In these last examples we are immediately aware of forces upon us due to our motion, and we interpret these motions from our own viewpoint, not that of an impartial observer attached to the universe.
The question then arises as to how to connect these experiences in accelerating frames with Newton's laws that are not formulated for such situations. The answer lies in the introduction of inertial forces, which are forces observed in the accelerating reference frame, due to its motion, but are not forces recognized in an inertial frame. These inertial forces are included in Newton's laws of motion, and with their inclusion Newton's laws work just as they would in an inertial frame. Centrifugal force is one of these inertial forces, the other two being the Coriolis force and the Euler force.
The way inertial forces work is illustrated below by a few examples.
Rotating spheres
Consider two identical balls isolated in space, but connected by a rope. We ignore any effects of gravity. We observe the tension in the rope, for example, by placing a spring in the center of the rope and measuring its stretch when the rope is under tension. We sit at the center of the rope and inquire whether the two balls are rotating about us.
This thought experiment was devised by Newton, who wanted to explore the question of whether we could discover that the balls were rotating even though we had no point of reference from which to infer that rotation was underway. He concluded that an observed tension in the rope would allow us to infer that the balls are rotating.
It is clear that the tension in the rope, as indicated by the stretch of the spring, is an incontrovertible observation that any observer would see, regardless of whether they were stationary or rotating with the balls.
Let us now look at this tension from the viewpoint of the inertial observers: they see the balls rotating with an angular rate of (say) ω radians/s. That means the balls have a speed of v = ωR where 2R is the separation of the centers of the balls. Their circular motion means that each ball is subject to an inward centripetal force provided by the tension in the rope, of magnitude FT = mv2/R = mRω2, and the measured stretch of the spring reflects exactly this force.
Next, let's look at things from the viewpoint of the rotating observers sitting at the center of the rope. They see the balls as stationary, because they are rotating with them. Because they rotate at the same rate as the spheres, they are said to be in a co-rotating frame. But they also see the stretched spring. Despite the tension from the stretched string, the balls do not move, so they are subject to no net force. The rotating observers succeed in using Newton's laws to explain the tension despite no motion, and to explain no motion despite the tension because, in their rotating frame, they experience a centrifugal force, an outward force radiating from their center position that affects all bodies they observe (including themselves if they move off-center). This centrifugal radially outward force on objects at distance R is of magnitude mRω2, but of course, these rotating observers simply see that this is the tension in the spring, and they cannot calculate its magnitude from scratch because they cannot measure the rotational rate ω.
However, if they are quite sophisticated, the rotating observers will notice that the centrifugal force they observe on every object they measure has some peculiar properties not shared by forces like gravity, or electrical forces. In particular, it has no observable source in a mass or a charge, like other physical forces, and appears to become larger the further you go from its radiating center, instead of weakening with distance like other forces. So they might conclude that this is an inertial force and try to explain their observations based upon their frame seen as a rotating frame, and calculate their rate of rotation using the measured tension and the formula FT = mRω2. If they did that, then their calculations would be mapped into an inertial frame, and they would analyze the situation the same way as an inertial observer. They then would use centripetal force instead of centrifugal force in their calculations, but as they move about in their rotating frame, their immediate visceral experience of the centrifugal force will be a real part of their everyday experience.
Whirling table
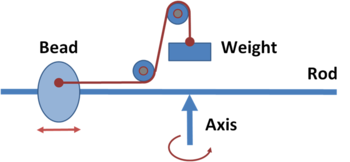
An apparatus called a "whirling table" consists of a rod that can be whirled about an axis, causing a bead to slide on the rod under the influence of centrifugal force.[1] A cord ties a weight to the sliding bead.
In a frame co-rotating with the rod, equilibrium is achieved when the inward force on the bead due to the weight exactly counterbalances the outward centrifugal force upon the bead. By observing changes in the equilibrium balancing distance for a given weight, or the variation of the weight at a fixed distance, the centrifugal force can be measured under changing conditions and used to infer the rate of rotation, which is not observable in a co-rotating frame.
From the viewpoint of an inertial (non-rotating) frame of reference, equilibrium results when the bead is positioned in the particular circular orbit for which the weight provides the correct centripetal force. By observing how the equilibrium balancing distance varies with the weight and the speed of rotation, the centripetal force can be measured as a function of the rate of rotation and the distance of the bead from the center of rotation.