User:John R. Brews/WP Import: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>John R. Brews
No edit summary
imported>John R. Brews
No edit summary
Line 1: Line 1:
A '''frame of reference''' in [[physics]], may refer to a ''[[coordinate system]]''  or [[Cartesian coordinate system|set of axes]] within which to measure the position, [[orientation (geometry)|orientation]], and other properties of objects in it, or it may refer to an ''observational reference frame'' tied to the state of motion of an [[Observer (special relativity)|observer]].
[[Image:Nullore bilanciato.svg|right|200px|thumb|Nullor electronic symbol (balanced version)]]
It may also refer to both an observational reference frame and an attached coordinate system, as a unit.
[[Image:Nullore sbilanciato.svg|right|200px|thumb|Nullor electronic symbol (unbalanced version)]]


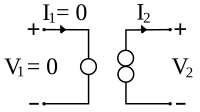
==Different aspects==
A '''nullor''' is a theoretical [[two-port network]] composed of a [[nullator]] at its input and a [[norator]] at its output.<ref>The name "nullor" was introduced by H.J. Carlin, ''Singular network elements'', IEEE Trans. Circuit Theory, March 1965, vol. CT-11, pp. 67-72.</ref> Nullors represent an ideal [[amplifier]], having infinite [[Electronic_amplifier#Input_and_output_variables|current, voltage, transconductance and transimpedance]] gain.<ref name=Verhoeven>
{{cite book
|author=Verhoeven C J M van Staveren A Monna G L E Kouwenhoven M H L & Yildiz E
|title=Structured electronic design: negative feedback amplifiers
|year= 2003
|publisher=Kluwer Academic
|location=Boston/Dordrecht/London
|isbn=1402075901
|pages=§2.2.2 pp. 32–34
|url=http://books.google.com/books?id=p8wDptzCMrUC&pg=PA24&dq=isbn:1402075901&sig=cxJIK6hgY7wKfWc7cV6ZVHT-iDc#PPA32,M1}}
</ref> Its [[Two-port_network#ABCD-parameters|transmission parameters]] are all zero, that is, its input-output behavior is summarized with the matrix:
::<math>
\begin{pmatrix}
v_1\\
i_1
\end{pmatrix}
=
\begin{pmatrix}
  0 & 0 \\
  0 & 0
\end{pmatrix}
\begin{pmatrix}
v_2\\
i_2
\end{pmatrix}


The need to distinguish between the various meanings of "frame of reference" has led to a variety of terms. For example, sometimes the type of coordinate system is attached as a modifier, as in ''Cartesian frame of reference''. Sometimes the state of motion is emphasized, as in ''[[Rotating reference frame|rotating frame of reference]]''. Sometimes the way it transforms to frames considered as related is emphasized as in ''Galilean frame of reference''. Sometimes frames are distinguished by the scale of their observations, as in ''macroscopic'' and ''microscopic frames of reference''.<ref name=macroscopic>The distinction between macroscopic and microscopic frames shows up, for example, in electromagnetism where [[Constitutive equation|constitutive relations]] of various time and length scales are used to determine the current and charge densities entering [[Maxwell's equations]]. See, for example, {{cite book |title=Electromagnetic and Optical Pulse Propagation 1: Spectral Representations in Temporally Dispersive Media |author=Kurt Edmund Oughstun |pages=p. 165 |url=http://books.google.com/books?id=behRnNRiueAC&pg=PA165&dq=macroscopic+frame++electromagnetism&lr=&as_brr=0&sig=ACfU3U3J6a2ZwvTOx7T3S6Zunptf9E9nxQ
|isbn=038734599X |year=2006 |publisher=Springer }}. These distinctions also appear in thermodynamics. See {{cite book |title=Classical Theory |author=Paul McEvoy |pages=p. 205 |url=http://books.google.com/books?id=dj0wFIxn-PoC&pg=PA206&dq=macroscopic+frame&lr=&as_brr=0&sig=ACfU3U2JFNgXVpz6Ew6hmp2rmdL6p9O7Ng#PPA205,M1
\ . </math>
|isbn=1930832028 |year=2002 |publisher=MicroAnalytix  }}.</ref>
In [[negative feedback]] circuits, the circuit surrounding the nullor determines the nullor output in such a way as to force the nullor input to zero.


In this article the term ''observational frame of reference'' is used when emphasis is upon the ''state of motion'' rather than upon the coordinate choice or the character of the observations or observational apparatus. In this sense, an observational frame of reference allows study of the effect of motion upon an entire family of coordinate systems that could be attached to this frame. On the other hand, a ''coordinate system'' may be employed for many purposes where the state of motion is not the primary concern. For example, a coordinate system may be adopted to take advantage of the symmetry of a system. In a still broader perspective, of course, the formulation of many problems in physics employs ''[[generalized coordinates]]'', ''[[normal modes]]'' or ''[[eigenvectors]]'', which are only indirectly related to space and time. It seems useful to divorce the various aspects of a reference frame for the discussion below. We therefore take observational frames of reference, coordinate systems, and observational equipment as independent concepts, separated as below:
Inserting a nullor in a circuit schematic imposes mathematical constraints on how that circuit must behave, forcing the circuit itself to adopt whatever arrangements are needed to meet the conditions. For example, an ideal [[op amp]] can be modeled using a nullor,<ref name=Verhoeven2>{{cite book
|author=Verhoeven C J M van Staveren A Monna G L E Kouwenhoven M H L & Yildiz E
|title=§2.6
|isbn=1402075901
|url=http://books.google.com/books?id=p8wDptzCMrUC&pg=PA24&dq=isbn:1402075901&sig=cxJIK6hgY7wKfWc7cV6ZVHT-iDc#PPA43,M1}}
</ref> and the textbook analysis of a feedback circuit using an ideal op amp uses the mathematical conditions imposed by the nullor to analyze the circuit surrounding the op amp.


*An observational frame (such as an [[inertial frame]] or [[non-inertial frame of reference]]) is a physical concept related to state of motion.
== Example: voltage-controlled current sink ==
[[Image:Current sink.PNG|thumbnail|250px|Figure 1: Operational-amplifier based current sink. Because the op amp is modeled as a nullor, op amp input variables are zero regardless of the values for its output variables.]]
Figure 1 shows a voltage-controlled current sink.<ref name=Spencer>
{{cite book
|author=Richard R Spencer & Ghausi MS
|title=Introduction to electronic circuit design
|year= 2003
|publisher=Prentice Hall/Pearson Education
|location=Upper Saddle River NJ
|isbn=0-201-36183-3
|pages=§5.1.6 pp. 226–227
|url=http://worldcat.org/isbn/0-201-36183-3}}
</ref> The sink is intended to draw the same current ''i<sub>OUT</sub>'' regardless of the applied voltage ''V<sub>CC</sub>'' at the output. The value of current drawn is to be set by the input voltage ''v<sub>IN</sub>''. Here the sink is to be analyzed by idealizing the op amp as a nullor.


*A coordinate system is a mathematical concept, amounting to a choice of language used to describe observations.<ref name =Pontriagin>
Using properties of the input nullator portion of the nullor, the input voltage across the op amp input terminals is zero. Consequently, the voltage across reference resistor ''R<sub>R</sub>'' is the applied voltage ''v<sub>IN</sub>'', making the current in  ''R<sub>R</sub>'' simply ''v<sub>IN</sub> / R<sub>R</sub>''. Again using the nullator properties, the input current to the nullor is zero. Consequently, [[Kirchhoff's current law]] at the emitter provides an emitter current of ''v<sub>IN</sub> / R<sub>R</sub>''. Using properties of the norator output portion of the nullor, the nullor provides whatever current is demanded of it, regardless of the voltage at its output. In this case, it provides the transistor base current ''i<sub>B</sub>''. Thus, Kirchhoff's current law applied to the transistor as a whole provides the output current drawn through resistor ''R<sub>C</sub>'' as:


In very general terms, a coordinate system is a set of arcs ''x''<sup>i</sup> = ''x''<sup>i</sup> (''t'') in a complex [[Lie group]]; see {{cite book |author=Lev Semenovich Pontri͡agin |title=L.S. Pontryagin: Selected Works Vol. 2: Topological Groups |pages= p. 429 |year=  |url=http://books.google.com/books?id=JU0DT_wXu2oC&pg=PA429&dq=algebra+%22coordinate+system%22&lr=&as_brr=0&sig=ACfU3U07j7JfzfwMigYTa2iDVygAb0WKCA
::<math> i_{OUT} = \frac {v_{IN}} {R_{R}} -i_B \ , </math>
|isbn=2881241336 |publisher=Gordon and Breach|edition=3rd ed }}. Less abstractly, a coordinate system in a space of n-dimensions is defined in terms of a basis set of vectors {'''e'''<sub>1</sub>, '''e'''<sub>2</sub>,… '''e'''<sub>n</sub>}; see {{cite book |title=Linear Algebra: A Geometric Approach |author= Edoardo Sernesi, J. Montaldi |pages=p. 95 |url=http://books.google.com/books?id=1dZOuFo1QYMC&pg=PA95&dq=algebra+%22coordinate+system%22&lr=&as_brr=0&sig=ACfU3U1TD6WmY73w4hEYlVFcXK5NxtKSDQ
|isbn=0412406802 |year=1993 |publisher=CRC Press  }} As such, the coordinate system is a mathematical construct, a language, that may be related to motion, but has no necessary connection to motion.


</ref> Consequently, an observer in an observational frame of reference can choose to employ any coordinate system (Cartesian, polar, curvilinear, generalized, …) to describe observations made from that frame of reference. A change in the choice of this coordinate system does not change an observer's state of motion, and so does not entail a change in the observer's ''observational'' frame of reference. This viewpoint can be found elsewhere as well.<ref name=Johansson>
where the base current of the bipolar transistor ''i<sub>B</sub>'' is normally negligible provided the transistor remains in [[Bipolar_junction_transistor#Regions_of_operation|active mode]]. That is, based upon the idealization of a nullor, the output current is controlled by the user-applied input voltage ''v<sub>IN</sub>'' and the designer's choice for the reference resistor ''R<sub>R</sub>''.
{{cite book |title=Unification of Classical, Quantum and Relativistic Mechanics and of the Four Forces |author=J X Zheng-Johansson and Per-Ivar Johansson
|pages=p. 13
|url=http://books.google.com/books?id=I1FU37uru6QC&pg=PA13&dq=frame+coordinate+johansson&lr=&as_brr=0&sig=ACfU3U1VAkGbfRjt_GTknoX6WRLWP-AVZw
|isbn=1594542600
|publisher=Nova Publishers
|year=2006  }}</ref> Which is not to dispute that some coordinate systems may be a better choice for some observations than are others.


*Choice of what to measure and with what observational apparatus is a matter separate from the observer's state of motion and choice of coordinate system.
The purpose of the transistor in the circuit is to reduce the portion of the current in ''R<sub>R</sub>'' supplied by the op amp. Without the transistor, the current through ''R<sub>C</sub>'' would be ''i<sub>OUT</sub> = ( V<sub>CC</sub> − v<sub>IN</sub> ) / R<sub>C</sub>'', which interferes with the design goal of independence of ''i<sub>OUT</sub>'' from ''V<sub>CC</sub>''. Another practical advantage of the transistor is that the op amp must deliver only  the small transistor base current, which is unlikely to tax the op amp's current delivery capability. Of course, only real op amps are current-limited, not nullors.


Here is a quotation applicable to moving observational frames <math>\mathfrak{R}</math> and various associated Euclidean three-space coordinate systems [''R'', ''R' '', ''etc.'']:
The remaining variation of the current with the voltage ''V''<sub>CC</sub>  is due to the [[Early effect]], which causes the β of the transistor to change with its collector-to-base voltage ''V''<sub>CB</sub> according to the relation β = β<sub>0</sub> ( 1 + ''V''<sub>CB</sub> / ''V''<Sub>A</sub> ), where ''V''<sub>A</sub> is the so-called Early voltage. Analysis based upon a nullor leads to the [[output resistance]] of this current sink as ''R''<sub>out</sub> = r<sub>O</sub> ( β + 1 ) + ''R''<sub>C</sub> , where r<sub>O</sub> is the small-signal transistor output resistance given by r<sub>O</sub> = ( ''V''<sub>A</sub> + ''V''<sub>CB</sub> ) / ''i''<sub>out</sub>. See [[Current_mirror#Output_resistance_3|current mirror]] for the analysis.
<ref name=Lyle >{{cite book  |title=Handbook of Continuum Mechanics: General Concepts, Thermoelasticity |pages= p. 9 |author=Jean Salençon, Stephen Lyle |url=http://books.google.com/books?id=H3xIED8ctfUC&pg=PA9&dq=physical+%22frame+of+reference%22&lr=&as_brr=0&sig=ACfU3U1tEWQICZdsXeuLyfmH2PoLgZnMGA
|isbn=3540414436 |year=2001 |publisher=Springer  }}</ref>


{{Cquote|We first introduce the notion of ''reference frame'', itself related to the idea of ''observer'': the reference frame is, in some sense, the "Euclidean space carried by the observer". Let us give a more mathematical definition:… the reference frame is... the set of all points in the Euclidean space with the rigid body motion of the observer. The frame, denoted <math>\mathfrak{R}</math>, is said to move with the observer.… The spatial positions of particles are labelled relative to a frame <math>\mathfrak{R}</math> by establishing a ''coordinate system'' ''R'' with origin ''O''. The corresponding set of axes, sharing the rigid body motion of the frame <math>\mathfrak{R}</math>, can be considered to give a physical realization of <math>\mathfrak{R}</math>. In a frame <math>\mathfrak{R}</math>, coordinates are changed from ''R'' to ''R''' by carrying out, at each instant of time, the same coordinate transformation on the components of ''intrinsic'' objects (vectors and tensors) introduced to represent physical quantities ''in this frame''.| Jean Salençon, Stephen Lyle ''Handbook of Continuum Mechanics: General Concepts, Thermoelasticity''}}
Use of the nullor idealization allows design of the circuitry around the op amp. The practical problem remains of designing an op amp that behaves like a nullor.
and this on the utility of separating the notions of <math>\mathfrak{R}</math> and [''R'', ''R' '', ''etc.'']:<ref name= Lakhtakia>{{cite book |title=Essays on the Formal Aspects of Electromagnetic Theory |author=Patrick Cornille |editor=Akhlesh Lakhtakia., ed |pages=p. 149 |url=http://books.google.com/books?id=qsOBhKVM1qYC&pg=PA149&dq=coordinate+system+%22reference+frame%22&lr=&as_brr=0&sig=ACfU3U0xhpZ2lI99UPiYQCOL6oJ0ALO5uA
|isbn=9810208545 |year=1993 |publisher=World Scientific  }}</ref>
{{Cquote|As noted by Brillouin, a distinction between mathematical sets of coordinates and physical frames of reference must be made. The ignorance of such distinction is the source of much confusion… the dependent functions such as velocity for example, are measured with respect to a physical reference frame, but one is free to choose any mathematical coordinate system in which the equations are specified.|L. Brillouin in ''Relativity Reexamined'' (quoted by Patrick Cornille) }}
and this, also on the distinction between <math>\mathfrak{R}</math> and [''R'', ''R' '', ''etc.'']:<ref name= Nerlich>{{cite book |title=What Spacetime Explains: Metaphysical essays on space and time |author=Graham Nerlich |pages=p. 64 |url=http://books.google.com/books?id=fKK7rKOpc7AC&pg=PA64&dq=%22idea+of+a+reference+frame%22&lr=&as_brr=0&sig=ACfU3U2wsO42pqLOJ453eeIzk7ztXTa6uQ
|isbn=0521452619 |year=1994 |publisher=Cambridge University Press}}</ref>


{{Cquote|The idea of a reference frame is really quite different from that of a coordinate system. Frames differ just when they define different ''spaces'' (sets of ''rest'' points) or times (sets of simultaneous events). So the ideas of a space, a time, of rest and simultaneity, go inextricably together with that of frame. However, a mere shift of origin, or a purely spatial rotation of space coordinates results in a new coordinate system. So frames correspond at best to ''classes'' of coordinate systems.|Graham Nerlich: ''What Spacetime Explains''}}
==References==
 
<references/>
and from J. D. Norton:<ref name=Norton>
 
{{cite journal |journal=Rep. Prog. Phys.|author=John D. Norton |year=1993 |volume=vol. 56 |pages=pp. 835-837 |title=General covariance and the foundations of general relativity: eight decades of dispute |url=http://www.pitt.edu/~jdnorton/papers/decades.pdf}}
 
</ref>
 
{{Cquote|In traditional developments of special and general relativity it has been customary not to distinguish between two quite distinct ideas. The first is the notion of a coordinate system, understood simply as the smooth, invertible assignment of four numbers to events in spacetime neighborhoods. The second, the frame of reference, refers to an idealized system used to assign such numbers …  To avoid unnecessary restrictions, we can divorce this arrangement from metrical notions. … Of special importance for our purposes is that each frame of reference has a definite state of motion at each event of spacetime.…Within the context of special relativity and as long as we restrict ourselves to frames of reference in inertial motion, then little of importance depends on the difference between an inertial frame of reference and the inertial coordinate system it induces. This comfortable circumstance ceases immediately once we begin to consider frames of reference in nonuniform motion even within special relativity.…More recently, to negotiate the obvious ambiguities of Einstein’s treatment, the notion of frame of reference has reappeared as a structure distinct from a coordinate system.|John D. Norton: ''General Covariance and the Foundations of General Relativity}}
 
The discussion is taken beyond simple space-time coordinate systems by Brading and Castellani.<ref name=Brading>
 
{{cite book |title=Symmetries in Physics: Philosophical Reflections |author=Katherine Brading & Elena Castellani |pages=p. 417 |url=http://books.google.com/books?id=SnmBN64cAdYC&pg=PA417&dq=%22idea+of+a+reference+frame%22&lr=&as_brr=0&sig=ACfU3U1PdXJdmFyMRiDb7xPDAI_dy9MgJg |isbn=0521821371 |year=2003 |publisher=Cambridge University Press}}
 
</ref> Extension to coordinate systems using generalized coordinates underlies the [[Hamilton's principle|Hamiltonian]] and [[Lagrangian]] formulations<ref name=Johns>
 
{{cite book |title=Analytical Mechanics for Relativity and Quantum Mechanics |pages=Chapter 16 |author=Oliver Davis Johns |url=http://books.google.com/books?id=PNuM9YDN8CIC&pg=PA318&dq=coordinate+observer&lr=&as_brr=0&sig=ACfU3U3TRrg4EVCiIW8btVgFdR49PD9RUg#PPA276,M1
|isbn=019856726X |year=2005 |publisher=Oxford University Press |nopp=true }}
 
</ref> of [[quantum field theory]], [[classical mechanics|classical relativistic mechanics]], and [[quantum gravity]].<ref name=Greenwood>
 
{{cite book |title=Classical dynamics |author=Donald T Greenwood |pages=p. 313 |year=1997 |edition=Reprint of 1977 Prentice-Hall ed |publisher=Courier Dover Publications |url=http://books.google.com/books?id=x7rj83I98yMC&pg=RA2-PA314&dq=%22relativistic+%22+Lagrangian+OR+Hamiltonian&lr=&as_brr=0&sig=ACfU3U3l7hGibLCCG40qWuiO3A5sN7E7lg#PRA2-PA313,M1
|isbn=0486696901 }}
 
</ref><ref name=Trump>
 
{{cite book |title=Classical Relativistic Many-Body Dynamics |author=Matthew A. Trump & W. C. Schieve |pages= p. 99 |url=http://books.google.com/books?id=g2yfLOp0IzwC&pg=PA99&dq=relativity+%22generalized+coordinates%22&lr=&as_brr=0&sig=ACfU3U230ux_i1Ov3QHf_xy1dAA_oLSKpw#PPA99,M1
|year=1999 |publisher=Springer |isbn= 079235737X }}
 
</ref><ref name=Kompaneyets>
 
{{cite book |author=A S Kompaneyets |title=Theoretical Physics |url=http://books.google.com/books?id=CQ2gBrL5T4YC&pg=PA118&dq=relativity+%22generalized+coordinates%22&lr=&as_brr=0&sig=ACfU3U3OOAmAAh2wV46vG0gUN0wSIPiIww
|pages=p. 118 |isbn=0486495329 |year=2003 |publisher=Courier Dover Publications |edition=Reprint of 2nd 1962 ed }}</ref><ref name=Srednicki>{{cite book |title=Quantum Field Theory |pages= Chapter 4|author=M Srednicki |publisher=Cambridge University Press |year=2007 |isbn=978-0-521-86449-7 |url=http://books.google.com/books?id=5OepxIG42B4C&pg=PA266&dq=isbn=9780521864497&sig=ACfU3U2J9PylxA2eptc48_TBT2u2GPfnVA#PPA31,M1 |nopp=true }}
 
</ref><ref name=Rovelli>
 
{{cite book |title=Quantum Gravity |author=Carlo Rovelli |pages= pp. 98 ''ff'' |url=http://books.google.com/books?id=HrAzTmXdssQC&pg=PA179&dq=%22relativistic+%22+Lagrangian+OR+Hamiltonian&lr=&as_brr=0&sig=ACfU3U3TLyr3CXsHYKFUGDe1dpq5ZWm_kg#PPA98,M1
|isbn=0521837332 |year=2004 |publisher=Cambridge University Press    }}</ref>
 
===Coordinate systems===
 
Although the term "coordinate system" is often used (particularly by physicists) in a nontechnical sense, the term "coordinate system" does have a precise meaning in mathematics, and sometimes that is what the physicist means as well.
 
A coordinate system in mathematics is a facet of [[geometry]] or of [[algebra]],<ref name=Barker>{{cite book |title=Continuous symmetry: from Euclid to Klein |author=William Barker & Roger Howe |pages=pp. 18 ''ff'' |url=http://books.google.com/books?id=NIxExnr2EjYC&pg=PA17&dq=geometry++axiom+%22coordinate+system%22&lr=&as_brr=0&sig=ACfU3U1-Tq9AjjikB_HSYJ1Xn0fFdHWY0g#PPA18,M1
|isbn=0821839004 |year=2008 |publisher=American Mathematical Society }}</ref><ref name=Ramsay>{{cite book |title=Introduction to Hyperbolic Geometry |author=Arlan Ramsay & Robert D. Richtmyer |pages=p. 11 |url=http://books.google.com/books?id=UVozmKVh7GsC&pg=PA202&dq=geometry++axiom+%22coordinate+system%22&lr=&as_brr=0&sig=ACfU3U0Nr0kKmV8XtorU41jRiiEo2wil3Q#PPA11,M1
|isbn=0387943390 |publisher=Springer |year=1995  }}</ref> in particular, a property of [[manifold]]s (for example, in physics, [[configuration space]]s or [[phase space]]s).<ref name=Hawking>According to Hawking and Ellis: "A manifold is a space locally similar to Euclidean space in that it can be covered by coordinate patches. This structure allows differentiation to be defined, but does not distinguish between different coordinate systems. Thus, the only concepts defined by the manifold structure are those that are independent of the choice of a coordinate system." {{cite book |title=The Large Scale Structure of Space-Time |author=Stephen W. Hawking & George Francis Rayner Ellis |isbn=0521099064 |year=1973 |publisher=Cambridge University Press |pages=p. 11 |url=http://books.google.com/books?id=QagG_KI7Ll8C&pg=PA59&dq=manifold+%22The+Large+Scale+Structure+of+Space-Time%22&lr=&as_brr=0&sig=ACfU3U1q-iaRTBDo6J8HMEsyPeFi8cJNWg#PPA11,M1
}} A mathematical definition is: ''A connected [[Hausdorff space]] ''M'' is called an ''n''-dimensional manifold if each point of ''M'' is contained in an open set that is homeomorphic to an open set in Euclidean ''n''-dimensional space.''</ref><ref name=Morita>{{cite book |title=Geometry of Differential Forms |author=Shigeyuki Morita, Teruko Nagase, Katsumi Nomizu |pages=p. 12 |url=http://books.google.com/books?id=5N33Of2RzjsC&pg=PA12&dq=geometry++axiom+%22coordinate+system%22&lr=&as_brr=0&sig=ACfU3U3Vi7xsLiYiWCK0erF6X2gczHOkJA#PPA12,M1
|isbn=0821810456 |year=2001 |publisher=American Mathematical Society Bookstore  }}</ref> The [[Cartesian coordinate system|coordinates]] of a point '''r''' in an ''n''-dimensional space are simply an ordered set of ''n'' numbers:<ref name=Korn>{{cite book |title=Mathematical handbook for scientists and engineers : definitions, theorems, and formulas for reference and review |author=Granino Arthur Korn, Theresa M. Korn |pages=p. 169 |url=http://books.google.com/books?id=xHNd5zCXt-EC&pg=PA169&dq=curvilinear+%22coordinate+system%22&lr=&as_brr=0&sig=ACfU3U3psSqwpBtA3U40e46VPPaMNMEw4g#PPA169,M1
|isbn=0486411478 |year=2000 |publisher=Courier Dover Publications}}</ref><ref name=encarta>See [http://encarta.msn.com/encyclopedia_761579532/Coordinate_System_(mathematics).html Encarta definition]. [http://www.webcitation.org/5kwcKb20f Archived] 2009-10-31.</ref>
:<math>\mathbf{r} =[x^1,\ x^2,\ \dots\ ,  x^n] \ .</math>
In a general [[Banach space]], these numbers could be (for example) coefficients in a functional expansion like a [[Fourier series]]. In a physical problem, they could be [[spacetime]] coordinates or [[normal mode]] amplitudes. In a [[Robotics|robot design]], they could be angles of relative rotations, linear displacements, or deformations of [[linkage (mechanical)|joints]].<ref name=Yamane>{{cite book |author=Katsu Yamane |title=Simulating and Generating Motions of Human Figures |isbn=3540203176 |year=2004 |publisher=Springer  |pages=12–13 |url=http://books.google.com/books?id=tNrMiIx3fToC&pg=PA12&dq=generalized+coordinates+%22kinematic+chain%22&lr=&as_brr=0&sig=ACfU3U3LRGJJTAHs21CHdOvuu08vw0cAuw#PPA13,M1  }}</ref> Here we will suppose these coordinates can be related to a [[Cartesian coordinate]] system by a set of functions:
:<math>x^j = x^j (x,\  y,\  z,\  \dots)\ , </math>&ensp; &ensp; <math> j = 1, \ \dots \ , \ n\  </math>
 
where ''x'', ''y'', ''z'', ''etc.'' are the ''n'' Cartesian coordinates of the point. Given these functions,  '''coordinate surfaces''' are defined by the relations:
:<math> x^j (x, y, z, \dots) = \mathrm{constant}\ , </math>&ensp; &ensp; <math> j = 1, \ \dots \ , \ n\  .</math>
The intersection of these surfaces define '''coordinate lines'''. At any selected point, tangents to the intersecting coordinate lines at that point define a set of '''basis vectors''' {'''e'''<sub>1</sub>, '''e'''<sub>2</sub>, …, '''e'''<sub>n</sub>} at that point. That is:<ref name=Papapetrou>{{cite book |title=Lectures on General Relativity |author=Achilleus Papapetrou |page=5 |url=http://books.google.com/books?id=SWeOggyp1ZsC&pg=PA3&dq=relativistic++%22general+coordinates%22&lr=&as_brr=0&sig=ACfU3U3sPmqPV3oEzbV5zHqErtZrqcx4bg#PPA5,M1
|isbn=9027705402 |year=1974 |publisher=Springer    }}</ref>
 
:<math>\mathbf{e}_i(\mathbf{r}) =\lim_{\epsilon \rightarrow 0} \frac{\mathbf{r}\left(x^1,\  \dots,\  x^i+\epsilon,\  \dots ,\  x^n \right) - \mathbf{r}\left(x^1,\  \dots,\  x^i,\  \dots ,\  x^n \right)}{\epsilon }\ ,</math>
 
which can be normalized to be of unit length. For more detail see [[Curvilinear_coordinates#Covariant_basis|curvilinear coordinates]].
 
Coordinate surfaces, coordinate lines, and [[Basis (linear algebra)|basis vectors]] are components of a '''coordinate system'''.<ref name=Zdunkowski>{{cite book |title=Dynamics of the Atmosphere |page=84  |isbn=052100666X |year=2003 |author=Wilford Zdunkowski & Andreas Bott |publisher=Cambridge University Press |url=http://books.google.com/books?id=GuYvC21v3g8C&pg=RA1-PA84&dq=%22curvilinear+coordinate+system%22&lr=&as_brr=0&sig=ACfU3U2g2k7kY5u-CVcJ1pH5ZxsbEb9Rig  }}</ref> If the basis vectors are orthogonal at every point, the coordinate system is an [[Orthogonal coordinates|orthogonal coordinate system]].


An important aspect of a coordinate system is its [[Metric (mathematics)|metric]] ''g''<sub>ik</sub>, which determines the [[arc length]] ''ds'' in the coordinate system in terms of its coordinates:<ref name=Borisenko>{{cite book |title=Vector and Tensor Analysis with Applications |author= A. I. Borisenko, I. E. Tarapov, Richard A. Silverman |page=86 |url=http://books.google.com/books?id=CRIjIx2ac6AC&pg=PA86&dq=coordinate+metric&lr=&as_brr=0&sig=ACfU3U1osXaT2hg7Md57cJ9katl3ttL43Q
[[Category:Electrical components]]
|isbn=0486638332 |publisher=Courier Dover Publications |year=1979  }}</ref>
[[Category:Control theory]]
[[Category:Electronics terms]]
[[Category:Signal processing]]
[[Category:Analog circuits]]
[[Category:Electronic design]]


:<math>(ds)^2 = g_{ik}\ dx^i\ dx^k \ , </math>


where repeated indices are summed over.
[[de:Nullor]]
 
[[it:Nullore]]
As is apparent from these remarks, a coordinate system is a [[Model theory|mathematical construct]], part of an [[axiomatic system]]. There is no necessary connection between coordinate systems and physical motion (or any other aspect of reality). However, coordinate systems can include time as a coordinate, and can be used to describe motion. Thus, [[Lorentz transformation]]s and [[Galilean transformation]]s may be viewed as [[Coordinate_system#Transformations|coordinate transformation]]s.
 
General and specific topics of coordinate systems can be pursued following the [[#See also|See also]] links below.
 
===Observational frames of reference===
 
An '''observational frame of reference''', often referred to as a ''physical frame of reference'', a ''frame of reference'', or simply a ''frame'', is a physical concept related to an [[Observer (special relativity)|observer]] and the observer's state of motion. Here we adopt the view expressed by Kumar and Barve: an observational frame of reference is characterized ''only by its state of motion''.<ref name=Kubar>See {{cite book |author=Arvind Kumar & Shrish Barve |page=115 |title=How and Why in Basic Mechanics |url=http://books.google.com/books?id=czlUPz38MOQC&pg=PA115&dq=%22characterized+only+by+its+state+of+motion%22+inauthor:Kumar&lr=&as_brr=0&sig=ACfU3U36HY3RerJYLWRlfJaGxRw7EqzIeA
|isbn=8173714207 |year= 2003 |publisher =Orient Longman}}</ref> However, there is lack of unanimity on this point. In special relativity, the distinction is sometimes made between an ''observer'' and a ''frame''. According to this view, a ''frame'' is an ''observer'' plus a coordinate lattice constructed to be an orthonormal right-handed set of spacelike vectors perpendicular to a timelike vector. See Doran.<ref name=Doran>{{cite book |url=http://www.worldcat.org/search?q=9780521715959&qt=owc_search |title=Geometric Algebra for Physicists |author= Chris Doran & Anthony Lasenby |page= §5.2.2, p. 133 |isbn=978-0-521-71595-9 |year=2003 |publisher=Cambridge University Press}}.</ref>  This restricted view is not used here, and is not universally adopted even in discussions of relativity.<ref name=Moller>For example, Møller states: "Instead of Cartesian coordinates we can obviously just as well employ general curvilinear coordinates for the fixation of points in physical space.…we shall now introduce general "curvilinear" coordinates ''x''<sup>i</sup> in four-space…." {{cite book |author=C. Møller |title=The Theory of Relativity |page=222 and p. 233 |year=1952 |publisher=Oxford University Press}}</ref><ref name=Lightman>{{cite book |title=Problem Book in Relativity and Gravitation  |author=Alan P. Lightman, R. H. Price & William H. Press |page=15  |url=http://books.google.com/books?id=YtxGYnnP1PEC&pg=PA15&dq=relativistic++%22general+coordinates%22&lr=&as_brr=0&sig=ACfU3U28SuvzlWcCJ7PXCY71TVn33GeBvA
|isbn=069108162X |publisher=Princeton University Press |year=1975  }}</ref> In [[general relativity]] the use of general coordinate systems is common (see, for example, the [[Karl Schwarzschild|Schwarzschild]] solution for the gravitational field outside an isolated sphere<ref name= Faber>{{cite book |title=Differential Geometry and Relativity Theory: an introduction |author=Richard L Faber |url=http://books.google.com/books?id=ctM3_afLuVEC&pg=PA149&dq=relativistic++%22general+coordinates%22&lr=&as_brr=0&sig=ACfU3U1_zMogoRkH1OhzpC77ULTkMN0ihg#PPA211,M1
|page=211 |isbn=082471749X |year=1983 |publisher=CRC Press  }}</ref>).
There are two types of observational reference frame: [[Inertial frame of reference|inertial]] and [[non-inertial reference frame|non-inertial]].
An inertial frame of reference is defined as one in which all laws of physics take on their simplest form. In [[special relativity]] these frames are related by [[Lorentz transformation]]s. In Newtonian mechanics, a more restricted definition requires only that [[Newton's first law]] holds true; that is, a Newtonian inertial frame is one in which a [[free particle]] travels in a [[straight line]] at constant [[speed]], or is at rest. These frames are related by [[Galilean transformation]]s. These relativistic and Newtonian transformations are expressed in spaces of general dimension in terms of [[Representation theory|representations]] of the [[Representation theory of the Poincaré group|Poincaré group]] and of the [[Representation theory of the Galilean group|Galilean group]].
 
In contrast to the inertial frame, a non-inertial frame of reference is one in which [[fictitious force]]s must be invoked to explain observations. An example is an observational frame of reference centered at a point on the Earth's surface. This frame of reference orbits around the center of the Earth, which introduces a fictitious force known as the [[Coriolis force]] (among others).
 
===Measurement apparatus===
A further aspect of a frame of reference is the role of the [[metrology|measurement apparatus]] (for example, clocks and rods) attached to the frame (see Norton quote above). This question is not addressed in this article, and is of particular interest in [[Measurement in quantum mechanics|quantum mechanics]], where the relation between observer and measurement is still under discussion (see [[measurement problem]]).
 
In physics experiments, the frame of reference in which the laboratory measurement devices are at rest is usually referred to as the [[laboratory frame]] or simply "lab frame." An example would be the frame in which the detectors for a particle accelerator are at rest. The lab frame in some experiments is an inertial frame, but it is not required to be (for example the laboratory in the surface of the Earth in many physics experiments is not inertial). In particle physics experiments, it is often useful to transform energies and momenta of particles from the lab frame where they are measured, to the [[center of momentum frame]] "COM frame" in which calculations are sometimes simplified, since potentially all kinetic energy still present in the COM frame may be used for making new particles. 
 
In this connection it may be noted that the clocks and rods often used to describe observers' measurement equipment in thought, in practice are replaced by a much more complicated and indirect [[metrology]] that is connected to the nature of the [[vacuum]], and uses [[atomic clocks]] that operate according to the [[standard model]] and that must be corrected for [[gravitational time dilation]].<ref name= Wolfson>{{cite book |author=  Richard Wolfson |title=Simply Einstein |url=http://books.google.com/books?id=OUJWKdlFKeQC&pg=PA216&dq=%22gravitational+time+dilation+%22&lr=&as_brr=0&sig=ACfU3U0_wc8IuNJdGCLnsaO-SyqXYaRapw
|page=216 |isbn=0393051544 |publisher=W W Norton & Co. |year=2003  }}</ref> (See [[second]], [[meter]] and [[kilogram]]).
 
In fact, Einstein felt that clocks and rods were merely expedient measuring devices and they should be replaced by more fundamental entities based upon, for example, atoms and molecules.<ref name=Rizzi>See {{cite book |title=Relativity in rotating frames |page=33 |url=http://books.google.com/books?id=_PGrlCLkkIgC&pg=PA226&dq=centrifugal+%22+%22+relativity+OR+relativistic&lr=&as_brr=0&sig=ACfU3U038RpTaZOnfjYn6zH9umefW7y_-Q#PPA33,M1
|isbn=1402018053 |year=2003 |publisher=Springer |author=Guido Rizzi, Matteo Luca Ruggiero  }}.</ref>
 
==Notes==
<references/>
[http://en.wikipedia.org/w/index.php?title=Frame_of_reference&diff=241548266&oldid=241417924 last edit by myself]
[http://en.wikipedia.org/w/index.php?title=Frame_of_reference&diff=227021176&oldid=225336594 first edit by myself]

Revision as of 11:58, 19 May 2011

Nullor electronic symbol (balanced version)
Nullor electronic symbol (unbalanced version)

A nullor is a theoretical two-port network composed of a nullator at its input and a norator at its output.[1] Nullors represent an ideal amplifier, having infinite current, voltage, transconductance and transimpedance gain.[2] Its transmission parameters are all zero, that is, its input-output behavior is summarized with the matrix:

In negative feedback circuits, the circuit surrounding the nullor determines the nullor output in such a way as to force the nullor input to zero.

Inserting a nullor in a circuit schematic imposes mathematical constraints on how that circuit must behave, forcing the circuit itself to adopt whatever arrangements are needed to meet the conditions. For example, an ideal op amp can be modeled using a nullor,[3] and the textbook analysis of a feedback circuit using an ideal op amp uses the mathematical conditions imposed by the nullor to analyze the circuit surrounding the op amp.

Example: voltage-controlled current sink

Figure 1: Operational-amplifier based current sink. Because the op amp is modeled as a nullor, op amp input variables are zero regardless of the values for its output variables.

Figure 1 shows a voltage-controlled current sink.[4] The sink is intended to draw the same current iOUT regardless of the applied voltage VCC at the output. The value of current drawn is to be set by the input voltage vIN. Here the sink is to be analyzed by idealizing the op amp as a nullor.

Using properties of the input nullator portion of the nullor, the input voltage across the op amp input terminals is zero. Consequently, the voltage across reference resistor RR is the applied voltage vIN, making the current in RR simply vIN / RR. Again using the nullator properties, the input current to the nullor is zero. Consequently, Kirchhoff's current law at the emitter provides an emitter current of vIN / RR. Using properties of the norator output portion of the nullor, the nullor provides whatever current is demanded of it, regardless of the voltage at its output. In this case, it provides the transistor base current iB. Thus, Kirchhoff's current law applied to the transistor as a whole provides the output current drawn through resistor RC as:

where the base current of the bipolar transistor iB is normally negligible provided the transistor remains in active mode. That is, based upon the idealization of a nullor, the output current is controlled by the user-applied input voltage vIN and the designer's choice for the reference resistor RR.

The purpose of the transistor in the circuit is to reduce the portion of the current in RR supplied by the op amp. Without the transistor, the current through RC would be iOUT = ( VCC − vIN ) / RC, which interferes with the design goal of independence of iOUT from VCC. Another practical advantage of the transistor is that the op amp must deliver only the small transistor base current, which is unlikely to tax the op amp's current delivery capability. Of course, only real op amps are current-limited, not nullors.

The remaining variation of the current with the voltage VCC is due to the Early effect, which causes the β of the transistor to change with its collector-to-base voltage VCB according to the relation β = β0 ( 1 + VCB / VA ), where VA is the so-called Early voltage. Analysis based upon a nullor leads to the output resistance of this current sink as Rout = rO ( β + 1 ) + RC , where rO is the small-signal transistor output resistance given by rO = ( VA + VCB ) / iout. See current mirror for the analysis.

Use of the nullor idealization allows design of the circuitry around the op amp. The practical problem remains of designing an op amp that behaves like a nullor.

References

  1. ↑ The name "nullor" was introduced by H.J. Carlin, Singular network elements, IEEE Trans. Circuit Theory, March 1965, vol. CT-11, pp. 67-72.
  2. ↑ Verhoeven C J M van Staveren A Monna G L E Kouwenhoven M H L & Yildiz E (2003). Structured electronic design: negative feedback amplifiers. Boston/Dordrecht/London: Kluwer Academic, §2.2.2 pp. 32–34. ISBN 1402075901. 
  3. ↑ Verhoeven C J M van Staveren A Monna G L E Kouwenhoven M H L & Yildiz E. §2.6. ISBN 1402075901. 
  4. ↑ Richard R Spencer & Ghausi MS (2003). Introduction to electronic circuit design. Upper Saddle River NJ: Prentice Hall/Pearson Education, §5.1.6 pp. 226–227. ISBN 0-201-36183-3. 


de:Nullor it:Nullore

Retrieved from "https://citizendium.org/wiki/index.php?title=User:John_R._Brews/WP_Import&oldid=816942"