Wasan: Difference between revisions
imported>Chunbum Park |
imported>Chunbum Park |
||
| Line 35: | Line 35: | ||
=== Types of problems === | === Types of problems === | ||
In the beginning, wasan included problems dealing with practical concerns, such as the calendar, which stimulated some of the most important findings in the studies of curves.<ref name="ogawa145">Ogawa, 2001.pp. 145</ref> Yoshida introduced the challenge of calculating the value of pi as an idai problem in a later edition of his ''Jinkoki''’s. The first to solve the problem was [[Muramatsu Shigekiyo]], who wrote in 1663 that π <math>= 3.14195264877</math>.<ref name="lavoisier">"Japanese mathematics in the Edo period (1600-1868) (Science networks. Historical studies)." Lavoisier Librairie. Web. 07 Dec. 2009. <http://www.lavoisier.fr>.</ref> He used the same technique that was used by [[Archimedes]] nineteen hundred years earlier, in which the value of pi is approximated on a regular polygon with a very large number of sides (in Muramatsu’s case, 32,768). [[Seki Takakazu]], Japan’s most celebrated mathematician, calculated a much more accurate value of pi to be 355/113, which was correct to the eleventh digit.<ref name="hidetoshirothman16">Hideotshi and Rothman, 2008. pp. 16</ref> He first used Muramatsu’s method to calculate the perimeters of three polygons with <math>2^1</math><math>^5</math>, <math>2^1</math><math>^6</math>, and <math>2^1</math><math>^7</math> sides respectively. Then he posited that the perimeter of an infinite-sided polygon, a.k.a. the circle, is the sum of a [[geometric series]] ( <math>a + ar + ar^2 + ar^3</math>…), which equals to <math>a/(1 - r)</math> with infinite number of terms | In the beginning, wasan included problems dealing with practical concerns, such as the calendar, which stimulated some of the most important findings in the studies of curves.<ref name="ogawa145">Ogawa, 2001.pp. 145</ref> Yoshida introduced the challenge of calculating the value of pi as an idai problem in a later edition of his ''Jinkoki''’s. The first to solve the problem was [[Muramatsu Shigekiyo]], who wrote in 1663 that π <math>= 3.14195264877</math>.<ref name="lavoisier">"Japanese mathematics in the Edo period (1600-1868) (Science networks. Historical studies)." Lavoisier Librairie. Web. 07 Dec. 2009. <http://www.lavoisier.fr>.</ref> He used the same technique that was used by [[Archimedes]] nineteen hundred years earlier, in which the value of pi is approximated on a regular polygon with a very large number of sides (in Muramatsu’s case, 32,768). [[Seki Takakazu]], Japan’s most celebrated mathematician, calculated a much more accurate value of pi to be 355/113, which was correct to the eleventh digit.<ref name="hidetoshirothman16">Hideotshi and Rothman, 2008. pp. 16</ref> He first used Muramatsu’s method to calculate the perimeters of three polygons with <math>2^1</math><math>^5</math>, <math>2^1</math><math>^6</math>, and <math>2^1</math><math>^7</math> sides respectively. Then he posited that the perimeter of an infinite-sided polygon, a.k.a. the circle, is the sum of a [[geometric series]] ( <math>a + ar + ar^2 + ar^3</math>…), which equals to <math>a/(1 - r)</math> with infinite number of terms: | ||
<blockquote>P(∞) = P(15) + a/(1-r) = P(16) + a<sub>1</sub> a<sub>2</sub> /( a<sub>1</sub> - a<sub>2</sub> ) = P(16) +<nowiki>[</nowiki> P(16) - P(15) <nowiki>][</nowiki> P(17) - P(16) <nowiki>] /{[</nowiki> P(16) - P(15) <nowiki>] - [</nowiki> P(17) - P(16) <nowiki>]}</nowiki></blockquote> | <blockquote>P(∞) = P(15) + a/(1-r) = P(16) + a<sub>1</sub> a<sub>2</sub> /( a<sub>1</sub> - a<sub>2</sub> ) = P(16) +<nowiki>[</nowiki> P(16) - P(15) <nowiki>][</nowiki> P(17) - P(16) <nowiki>] /{[</nowiki> P(16) - P(15) <nowiki>] - [</nowiki> P(17) - P(16) <nowiki>]}</nowiki></blockquote> | ||
He let a<sub>1</sub> equal the difference in the perimeters of <math>2^1</math><math>^5</math> and <math>2^1</math><math>^6</math>-sided polygons, a<sub>2</sub> equal the difference in the perimeters of <math>2^1</math><math>^6</math> and <math>2^1</math><math>^7</math>-sided polygons, and r equal the ratio of the differences, a<sub>2</sub> and a<sub>1</sub>. | |||
Seki evidently took great interest in the number theory, as his other achievements include discovering the theory of determinants, (see fig. 8) the Bernoulli numbers, and Horner’s method for extracting irrational roots before the European mathematicians who are given credit for originating them. (Hidetoshi and Rothman 69-71) He also devoted one of his seven books to the magic squares. In one example, Seki drew a filled 3 by 3 square like the one shown in fig. 9 and a blank 7 by 7 (which is 2n + 1, in which n = 3) square. Then he started numbering to the right from the cell next to the left of the upper right-hand corner until he reached n (in this case, number 3). Then he numbered left from the cell to the left of 1 until he reached the 2n-1 (in this case, number 5). Then he numbered down the right side to the cell preceding the lower right-hand one. Then he numbered along the top row until he reached the upper left-hand corner. Then he filled the left-hand column and the bottom row by subtracting from (2n + 1)2 + 1 the respective numbers on the opposite side. Then he switched n (in this case, 3) figures to the left of the upper right-hand corner with the corresponding ones in the lower row, and likewise for the n figures above the lower right hand corner, resulting in a square shown in fig. 11. Finally he filled the inner cells by repeating the procedure with number 13, resulting in the square shown in fig. 12, which includes all numbers from 1 to 49 and features consecutive patterns at intervals of 3 (10, 11, 12; 23, 25, 27; 43, 42, 41; 28, 36, 48). (Smith and Mikami 116-118) | Seki evidently took great interest in the number theory, as his other achievements include discovering the theory of determinants, (see fig. 8) the Bernoulli numbers, and Horner’s method for extracting irrational roots before the European mathematicians who are given credit for originating them. (Hidetoshi and Rothman 69-71) He also devoted one of his seven books to the magic squares. In one example, Seki drew a filled 3 by 3 square like the one shown in fig. 9 and a blank 7 by 7 (which is 2n + 1, in which n = 3) square. Then he started numbering to the right from the cell next to the left of the upper right-hand corner until he reached n (in this case, number 3). Then he numbered left from the cell to the left of 1 until he reached the 2n-1 (in this case, number 5). Then he numbered down the right side to the cell preceding the lower right-hand one. Then he numbered along the top row until he reached the upper left-hand corner. Then he filled the left-hand column and the bottom row by subtracting from (2n + 1)2 + 1 the respective numbers on the opposite side. Then he switched n (in this case, 3) figures to the left of the upper right-hand corner with the corresponding ones in the lower row, and likewise for the n figures above the lower right hand corner, resulting in a square shown in fig. 11. Finally he filled the inner cells by repeating the procedure with number 13, resulting in the square shown in fig. 12, which includes all numbers from 1 to 49 and features consecutive patterns at intervals of 3 (10, 11, 12; 23, 25, 27; 43, 42, 41; 28, 36, 48). (Smith and Mikami 116-118) | ||
Revision as of 23:52, 13 December 2009
Higher mathematics in pre-modern Japan, also known as wasan (和算), flourished during the Edo period from the early 17th to the late 19th centuries. It had its origins in the Chinese mathematical texts which were acquired by the Japanese during their invasions of Korea in the late 16th century.[1] In a fairly isolated state, the Japanese mathematicians were able to make brilliant new discoveries in areas rarely attributed to a non-Western scholarship, sometimes outpacing their Western counterparts.[2]
Studies of Japanese mathematics were prompted by the introduction of Western mathematics to Japan and the subsequent decline of wasan during the latter half of the 19th century. Despite the steady increase in the number of articles published in Japanese since the 1920s, the subject remained at the backstage because of postwar-Japan’s scientific national policy. This changed in the recent years with the revisionist historians who have sought to contradict the Eurocentric historical views by reevaluating the non-Western sciences.[3] In this revisionist discourse, the centerpiece has often consisted of China and Japan, both of which defied the West’s totalitarian portrait of the Orient[4] by building vibrant economies and achieving comparable scientific advances before the mid-1800s.[5]
Mathematics during the Asuka and Nara periods
The oldest known case of mathematics in Japan was a system of exponential notation for high powers of ten, similar to the exponential law , which was in use before Jimmu’s legendary founding of Japan in the seventh century BCE. Findings on the subsequent cases of mathematics in ancient Japan come from the 6th century CE and afterwards when Buddhism was introduced from Korea. During the reign of Empress Suiko, the Chinese chronological system was made known, books on astrology and the calendar were introduced, and the first almanacs came into use. Prince Shotoku was so engaged in these learnings that he was honored as the father of Japanese mathematics. Emperor Tenchi, who ruled from 668 to 671 CE, created a water clock and defined the length of a day as one hundred hours. Around this time, a school of arithmetic and an observatory were also established. In 701, Emperor Monbu established a university system that included mathematical studies based on nine Chinese texts.[6] The most important among them concerned algebra, which enabled the creation of the department of “Arithmetic Intelligence” responsible for land survey and tax collection in 718. Calculations of the period were done with small bamboo sticks known as sangi, which were arranged differently like the Roman numerals to represent different numbers and were placed on paper with prescribed operations.[7]
After this brief period of enthusiasm and progress, Japanese mathematics unfortunately stagnated and stalled for nine hundred years. The nine Chinese texts were eventually forgotten, and mathematics in Japan degenerated into a superstitious body of knowledge that concerned puzzles and fortune telling. It was said that the knowledge of division was lost except in some religious establishments where calendar manuscripts were found.[8] During the Kamakura and the Muromachi periods, occasional references to sangi indicate that its use continued, but no new developments materialized.[9]
Wasan during the Edo period
The Dark Age for Japanese mathematics ended with Toyotomi Hideyoshi’s invasion of Korea in 1592. A soldier was able to return to the port of Hakata with a Chinese abacus, which existed in China since the 1200s and became known as soroban in Japanese. (Palmer) Its use became widespread after Mori Shigeyoshi published an introductory text regarding the abacus in 1622, although it did not completely replace the sangi that was more convenient for complex algebraic operations.[10] A more extensive text, and also the first complete mathematics book in Japan, was published under the title, Jinkoki, or Large and Small Numbers, in 1627 by Yoshida Mitsuyoshi. It was based on a famous Chinese text that was published in 1593 and dealt mostly with methods of computations such as multiplication, division, and the extraction of square and cube roots on the abacus.[11] Yoshida published at least six new editions of the Jinkoki, and among them the 1641 edition was the beginning of idai,[1] in which open problems are presented to the readers at the end of the book.[12]
After this initial takeoff, Japanese mathematics steadily progressed, primarily in areas of geometry and number theory,[13] within an open intellectual dialogue that was initially facilitated and proliferated by the samurai class. At the onset, mathematics was mostly pursued by the samurais as it had military application in surveying, navigation, and calendar making.[14] As the samurais came to work as civil servants with modest stipends, they also taught reading, writing, and arithmetic in small private schools called juku, which comprised much of the educational system in pre-modern Japan. Because of the low attendance fees, juku’s were widely attended by members across all ages and economic strata, and consequently mathematics became widely accessible within the Japanese society. People who could not afford to publish their own books posted their new findings on wooden prayer tablets in temples as offering to the gods. These tablets, which became known as sangaku, allowed the Japanese mathematicians to exchange ideas and identify new problems and thus transformed the temples into intellectual forums facilitating a nationwide dialogue. This open and collaborative discourse also existed in publications through the practice of idai, and it accelerated advances in Japanese mathematics, which took tangible form as wasan by the end of the seventeenth century.[15]
How wasan was expressed
|
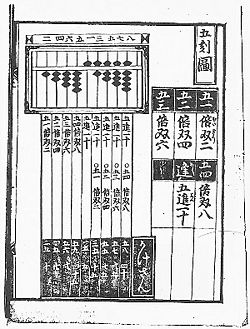
Example of mathematical notations in wasan: The number of vertical lines represent the coefficient; for example, "||" means "". 長 is designated as ; 短, ; and 中, . 巾 means , and 勾 means "/". |
How was wasan expressed and solved? It was written vertically in Kanbun, or classical Chinese, that served a similar role in East Asia as Latin in medieval Europe as the written language of higher culture.[16] Because there were only few symbols involved, more complicated equations had to be accompanied by sentences.[17] The traditional Japanese mathematicians did not discriminate between the rational and the irrational numbers, since they dealt with the physical representations of numbers directly on the abacus rather than converting them into decimals. This meant that, unlike their Western contemporaries,[18] the Japanese did not automatically assume π to consist of repeating decimals. It is also important to note that there was no concept of the Cartesian plane in wasan, which limited the understanding differential calculus for the Japanese.[19]
Types of problems
In the beginning, wasan included problems dealing with practical concerns, such as the calendar, which stimulated some of the most important findings in the studies of curves.[20] Yoshida introduced the challenge of calculating the value of pi as an idai problem in a later edition of his Jinkoki’s. The first to solve the problem was Muramatsu Shigekiyo, who wrote in 1663 that π .[21] He used the same technique that was used by Archimedes nineteen hundred years earlier, in which the value of pi is approximated on a regular polygon with a very large number of sides (in Muramatsu’s case, 32,768). Seki Takakazu, Japan’s most celebrated mathematician, calculated a much more accurate value of pi to be 355/113, which was correct to the eleventh digit.[22] He first used Muramatsu’s method to calculate the perimeters of three polygons with , , and sides respectively. Then he posited that the perimeter of an infinite-sided polygon, a.k.a. the circle, is the sum of a geometric series ( …), which equals to with infinite number of terms:
P(∞) = P(15) + a/(1-r) = P(16) + a1 a2 /( a1 - a2 ) = P(16) +[ P(16) - P(15) ][ P(17) - P(16) ] /{[ P(16) - P(15) ] - [ P(17) - P(16) ]}
He let a1 equal the difference in the perimeters of and -sided polygons, a2 equal the difference in the perimeters of and -sided polygons, and r equal the ratio of the differences, a2 and a1.
Seki evidently took great interest in the number theory, as his other achievements include discovering the theory of determinants, (see fig. 8) the Bernoulli numbers, and Horner’s method for extracting irrational roots before the European mathematicians who are given credit for originating them. (Hidetoshi and Rothman 69-71) He also devoted one of his seven books to the magic squares. In one example, Seki drew a filled 3 by 3 square like the one shown in fig. 9 and a blank 7 by 7 (which is 2n + 1, in which n = 3) square. Then he started numbering to the right from the cell next to the left of the upper right-hand corner until he reached n (in this case, number 3). Then he numbered left from the cell to the left of 1 until he reached the 2n-1 (in this case, number 5). Then he numbered down the right side to the cell preceding the lower right-hand one. Then he numbered along the top row until he reached the upper left-hand corner. Then he filled the left-hand column and the bottom row by subtracting from (2n + 1)2 + 1 the respective numbers on the opposite side. Then he switched n (in this case, 3) figures to the left of the upper right-hand corner with the corresponding ones in the lower row, and likewise for the n figures above the lower right hand corner, resulting in a square shown in fig. 11. Finally he filled the inner cells by repeating the procedure with number 13, resulting in the square shown in fig. 12, which includes all numbers from 1 to 49 and features consecutive patterns at intervals of 3 (10, 11, 12; 23, 25, 27; 43, 42, 41; 28, 36, 48). (Smith and Mikami 116-118)
Outside the publications, Japanese mathematics was usually limited to geometry problems that were found on the sangaku tablets. Geometry problems sometimes concerned beautiful arrangement of shapes, such as a fan, and solving them were considered as a type of art in itself.[20] Some geometric problems related to more practical concerns of architecture and woodcraft. One such case involved the lotus decorations of the Japanese temples from the Asuka and the Nara periods (538-794). As the lotus fruits were usually arranged in densest packaging within the receptacle, a practical artistic concern was the densest packing of circles within circles. The Japanese may also have had an interest in the densest packing problems because they addressed the practical issues of economical cuttings and arrangements of objects.[23] Geometry problems continued to evolve in more complex forms, until they eventually involved intersecting solids and surface areas.[24]
Wasan's decline and conclusion
Despite its substantial achievements, mathematics in Japan never led to a discovery of mechanical or physical laws as it has in the West. This was partly because mathematics was considered as more of a recreational art rather than science. The Japanese mathematicians also refused to denigrate their works as those of the artisans by solving problems relating to practical issues. Instead they focused on abstract problems, which made inevitable the displacement of wasan by western mathematics by the late Tokugawa period.[25]
notes
- ↑ Jump up to: 1.0 1.1 Okumura, 2009. pp. 79
- ↑ Ruttkay, 2008. pp. 1
- ↑ Ogawa, 2001.pp. 146-147
- ↑ Hobson, 2004. pp. 226
- ↑ Hanley, 1999. pp. 13
- ↑ Smith and Mikami, 1914. pp. 4-9
- ↑ Hideotshi and Rothman, 2008. pp. 10-12
- ↑ Smith and Mikami, 1914. pp. 14-15
- ↑ Hideotshi and Rothman, 2008. pp. 14
- ↑ Hideotshi and Rothman, 2008. pp. 19
- ↑ Smith and Mikami, 1914. pp. 38
- ↑ Hideotshi and Rothman, 2008. pp. 13-16
- ↑ Okumura, 2009. pp. 80
- ↑ Bartholomew, 1989. pp. 21
- ↑ Hideotshi and Rothman, 2008. pp. 19-21
- ↑ Hideotshi and Rothman, 2008. pp. 9
- ↑ Ogawa, 2001.pp. 140
- ↑ Hideotshi and Rothman, 2008. pp. 75
- ↑ Morimoto, 2009. pp. 132-133
- ↑ Jump up to: 20.0 20.1 Ogawa, 2001.pp. 145
- ↑ "Japanese mathematics in the Edo period (1600-1868) (Science networks. Historical studies)." Lavoisier Librairie. Web. 07 Dec. 2009. <http://www.lavoisier.fr>.
- ↑ Hideotshi and Rothman, 2008. pp. 16
- ↑ Tarnai and Miyazaki, 2003. pp. 145-149
- ↑ Okumura, 2009. pp. 81
- ↑ Ravina, 1993. pp. 205-207