Work (physics): Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer No edit summary |
||
| Line 125: | Line 125: | ||
where (ξ, η, ζ) is the acceleration of particle with mass ''m''. This is already the modern formula, but not yet the modern terminology. Navier published this formula in 1819, in a new edition of ''Architecture Hydraulique'', an old work (c. 1738) written by [[Forest de Bélidor]]. The old work was revised and extended by Navier, (who, parenthetically, referred to the 1779 work of Lazare Carnot). | where (ξ, η, ζ) is the acceleration of particle with mass ''m''. This is already the modern formula, but not yet the modern terminology. Navier published this formula in 1819, in a new edition of ''Architecture Hydraulique'', an old work (c. 1738) written by [[Forest de Bélidor]]. The old work was revised and extended by Navier, (who, parenthetically, referred to the 1779 work of Lazare Carnot). | ||
Much of the modern terminology [work (''travail'') is force times path (''chemin'')] was established by [[Gaspard-Gustave Coriolis]],<ref>G.-G. de Coriolis, ''Du Calcul de l'Effet des Machines'', Paris (1829). | Much of the modern terminology [work (''travail'') is force times path (''chemin'')] was established by [[Gaspard-Gustave Coriolis]],<ref>G.-G. de Coriolis, ''Du Calcul de l'Effet des Machines'', Paris (1829). Also the second edition of 1844 (see [http://books.google.nl/books?id=-mISAAAAIAAJ&dq=%22Du+Calcul+de+l%27effet+des+machines%22+Coriolis&source=gbs_navlinks_s Google books]) uses the term ''force vive'' and not ''énergie cinétique''.</ref> who gave the correct formula for change in kinetic energy, although he spoke of ''force vive'' (with factor ½), instead of kinetic energy (the latter term was coined by [[William Thomson]] around 1850). His terminology was taken over by [[Jean-Victor Poncelet]] who did much to propagate the terms, especially among engineers. | ||
==Reference== | ==Reference== | ||
<references /> | <references /> | ||
Revision as of 10:34, 5 July 2009
In physics, work is the energy that is transferred to a body when it is moved along a path by a force. When the force is conservative (non-dissipative) the work is independent of the path. Work done on a body is accomplished not only by a displacement of the body as a whole from one place to another but also, for example, by compressing a gas, by rotating a shaft, and even by directing small magnetic particles within a body along an external magnetic field.
As stated, work is a form of energy and consequently has dimension energy (force times length). In SI units the unit is joule; in cgs units it is erg.
The terms "work", "energy", and "force" have a well-defined, quantitative, meaning in physics, which differs somewhat from their more qualitative meaning in daily life. For instance, in physics work can be negative.
Definition of mechanical work
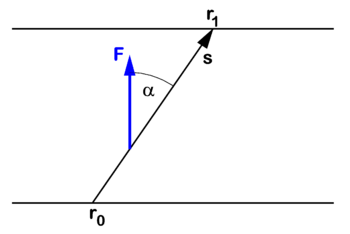
The mechanical work W is defined as force times path length: When a constant force F acts on a body along a straight path and the body is moved over a length |s| along this path, then
Here s is vector of magnitude |s| along the path. The dot product between the two vectors F and s is the product of their magnitudes |F| and |s| times the cosine of the angle, α, between the vectors.
When the force is directed along the path (F and s parallel), α = 0, cosα = 1, and we have simply W = |F| |s|. The positive work W is converted into an increase of kinetic energy T,
- W = ΔT ≡ T1 − T0 > 0.
In the next section this relation will be proved and shown to be a consequence of Newton's second law: F = m a.
When a force is perpendicular to the path, α = 90°, cosα = 0, the force performs no work. Examples of such a situation are the centrifugal force on a mass in uniform circular motion and the gravitational force acting on a satellite in a circular orbit. If a body is in uniform (i.e., has constant speed) straight motion and the only force acting on it is perpendicular to its path, then the body will persist in its uniform straight motion (Newton's first law).
When a force F is anti-parallel to the path (α = 180°), it performs negative work W < 0, since cosα = −1, and |F| and |s| are both greater than zero. The negative work done by the force is converted into a decrease of the kinetic energy T,
- W = ΔT < 0
(ΔT < 0 because T decreases, i.e., T1 < T0).
For example, think of an old-fashioned type of cannon that shoots a cannon ball of mass m straight up. The gun powder explosion gives the ball initial kinetic energy T0 = ½ m v02. The gravitational attraction of the earth performs negative work (force downward, motion of the cannon ball upward), until at the highest point the speed v1 and the kinetic energy T1 = ½ m v12 of the ball are zero. The amount of work performed is W = ΔT = 0−T0 = −T0. At the highest point the motion of the cannon ball reverts direction, it starts falling to earth, and from there on the gravitational attraction performs positive work (direction of motion and force are parallel). The kinetic energy increases again until it achieves its original value T0 = ½ m v02 at the point where the cannon ball arrives again at the cannon. The total work done by the gravitation is zero, the work done on the cannon ball going up cancels the work done on the ball going down. (In this example we ignore friction by the air).
When the the force is conservative (non-dissipative), the work is independent of path, and when furthermore the path is a closed curve, the total work is zero (one way the work is positive and the other way the work is equally large in absolute value, but negative).
As the gravitational field is conservative, we just saw an example of a mass (a cannon ball) making a closed path in a conservative force field. The potential energy U of a mass m close to the surface of the earth is equal to U = mgh, where g is the gravitational acceleration and h is the height. When the cannon is positioned at height h = 0, the cannon ball starts with potential energy zero, U0 = 0. The work W done by the gravitational field on the cannon ball going upward has two effects: it decreases its kinetic energy—as just discussed—and it increases its potential energy, U1 > U0, so that
- W = −ΔU ≡ −(U1 − U0) = U0 − U1 < 0.
At the highest point, h1, the potential energy is maximum U1 = mgh1 (equal to minus the work performed) and the kinetic energy is zero (this is the point where the motion of the cannon ball changes direction, for a small amount of time its speed is zero). The work done by a conservative force converts a decrease in kinetic energy into an increase of potential energy and conversely:
- W = ΔT = −ΔU, so that ΔT + ΔU = 0.
When the cannon ball dropping down is at height h = 0 again, its kinetic energy is maximum (equal to the energy imparted to it by the exploding gun powder) and its potential energy is zero again.
Example of mechanical work
- Work to lift a mass m in the gravitational field of the earth. Close to the surface of the earth, the attractive force is constant and equal to the gravitational acceleration g times m. The work W to lift the mass to a height h is,
- When h is positive, and the mass is at rest before and after the lifting (no change in kinetic energy), the work is completely converted into potential energy: U(h) = mgh.
Mathematical formulation
When the force is not constant along the path, or the path is not straight, it is possible to compute the work by infinitesimal calculus. One divides the path in N pieces Δsi, which are small enough to assume that the force is constant and the piece is straight. The (approximate) total work is obtained by summing the work done along the individual small pieces,
To improve the approximation one makes the pieces Δs smaller and smaller, so that their lengths go to zero. The limit is the path integral
where s0 is the tangent vector to the path at r(t0) ≡ r0 and s1 is tangent at the end point r1 of the path.
To show that the work is converted into an increase in kinetic energy, we write for one mass m
where we used F = m a (Newton's second law) and that the acceleration a is the second derivative of r with respect to time. Integrate
where we used that Δs is tangent to the path, i.e.,
and s0 = s(t0) and s1 = s(t1). Hence
To show that work by a conservative force is converted into decrease in potential energy, we use the relation between force and potential, valid for conservative fields
and by the chain rule
Integrate
In summary,
In total, the conservation of mechanical energy follows
History
The following remarks are mainly based on a paper by Grattan-Guinness.[1]
When Newton published his Principia in 1687 he, of course, defined implicitly energy and work. However, it took more than a century before these concepts were recognized amidst the equations and seen as useful and worthy of independent consideration. A quantity close to kinetic energy was noticed quite early; Leibniz coined the name vis viva (live force) in 1695 for the quantity mv2 that—except for the factor ½— is what we now call kinetic energy. The fact that Leibniz used the name "vis", which usually was restricted to mean "force", shows already that the concept of force was not fully grasped at that time either. Daniel Bernoulli wrote in 1753 about "live forces which the man produces during his work". He was close to the statement (proved earlier in this article) that work gives (a change of) kinetic energy (live force).
During the industrial revolution attention of many engineers and scientists became focused on machines (steam engines, watermills, windmills, etc.) that delivered useful work. In that context Lazare Carnot derived in 1779 a formula for the change in live forces that comes close to the modern equation. It contains the angle between the velocity (ds/dt) and the acceleration (F/m) and integrates over time, hence Carnot's formula is almost (in modern notation):
Next developments came from French physicists and engineers educated at the École Polytechnique, a school which was founded in revolutionary France (1794). Claude-Louis Navier, recognizing energy conservation, derived
where (ξ, η, ζ) is the acceleration of particle with mass m. This is already the modern formula, but not yet the modern terminology. Navier published this formula in 1819, in a new edition of Architecture Hydraulique, an old work (c. 1738) written by Forest de Bélidor. The old work was revised and extended by Navier, (who, parenthetically, referred to the 1779 work of Lazare Carnot).
Much of the modern terminology [work (travail) is force times path (chemin)] was established by Gaspard-Gustave Coriolis,[2] who gave the correct formula for change in kinetic energy, although he spoke of force vive (with factor ½), instead of kinetic energy (the latter term was coined by William Thomson around 1850). His terminology was taken over by Jean-Victor Poncelet who did much to propagate the terms, especially among engineers.
Reference
- ↑ I. Grattan-Guinness, Work for the Workers: Advances in Engineering Mechanics and Instruction in France, 1800-1830, Annals of Science, vol. 41, (1984), pp. 1–33
- ↑ G.-G. de Coriolis, Du Calcul de l'Effet des Machines, Paris (1829). Also the second edition of 1844 (see Google books) uses the term force vive and not énergie cinétique.