User:Boris Tsirelson/Sandbox1: Difference between revisions
imported>Boris Tsirelson |
imported>Boris Tsirelson |
||
| Line 134: | Line 134: | ||
such operations (higher order logic). In particular, third-order logic appears when dealing with all topologies on ''X''. Subsets of ''X'' may be treated as maps <math> X \to \{0,1\} </math>; sequences of points of ''X'' may be treated as maps <math> \{1,2,\dots\} \to X </math>. | such operations (higher order logic). In particular, third-order logic appears when dealing with all topologies on ''X''. Subsets of ''X'' may be treated as maps <math> X \to \{0,1\} </math>; sequences of points of ''X'' may be treated as maps <math> \{1,2,\dots\} \to X </math>. | ||
Using ''Isabelle/HOL'' syntax, Example 1 may be written as | Using ''Isabelle/HOL'' syntax, Example 1 may be written as {{nowrap|"<math>\forall</math>''x''::real. <math>\exists</math>''y''::real. <math>y^3=x</math>"}}, | ||
which is of first order. Second-order examples: "for every subset ''A'' of the real line" may be written as {{nowrap|"<math>\forall</math>''A''::real set"}} while "for every function ''f'' from the real line to itself" may be written as {{nowrap|"<math>\forall</math>''f''::{real}<math>\Rightarrow</math>real"}}. | which is of first order. Second-order examples: "for every subset ''A'' of the real line" may be written as {{nowrap|"<math>\forall</math>''A''::real set"}} while "for every function ''f'' from the real line to itself" may be written as {{nowrap|"<math>\forall</math>''f''::{real}<math>\Rightarrow</math>real"}}. | ||
Revision as of 07:59, 16 August 2010
For a mathematical theory, correctness means formalizability. "In practice, the mathematician ... is content to bring the exposition to a point where his experience and mathematical flair tell him that translation into formal language would be no more than an exercise of patience (though doubtless a very tedious one)."[1] Reliability of these experience and flair appears to be high but not perfect. Formalization is especially desirable in complicated cases, but feasible only in very simple cases, unless computers help. (Similarly, without computers a programmer is able to debug only very simple programs.)
A proof assistant is a computer program used interactively for developing human-readable reliable mathematical documents in a formal language. (It is not the same as a non-interactive, fully automated theorem prover.)
Isabelle/Isar
Nowadays (about 2010) the most successful project of this class combines
- Isabelle, a generic system for implementing logical formalisms;
- Isar (Intelligible SemiAutomated Reasoning), a versatile language environment for structured formal proofs;
- Proof General, a configurable user interface (front-end) for proof assistants;
- HOL (Higher-Order Logic).
Top 100 theorems in Isabelle + Formalizing 100 Theorems + Isabelle + Download and installation + Projects + The Isabelle2009-2 Library + IsarMathLib: A library of formalized mathematics for Isabelle/ZF
Example session
First impressions
An existing file, verified before, is used as the source text in this example. Thus, the session is not really interactive. However, this fact is not known to Isabelle. The proof assistant treats the session as interactive, and the text as new.
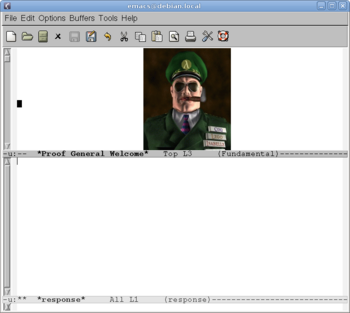
We start Proof General (Fig. 1) and enter the source text (Fig. 2).
On this stage Proof General does not send the text to Isabelle; we still can edit the text. Proof General helps us by automatic colorization according to the syntax of the Isar language.
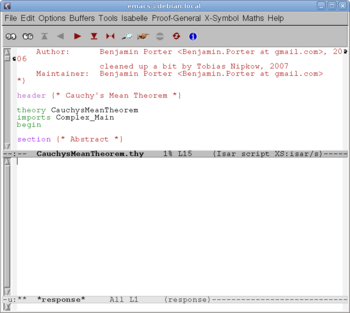
We start a new theory "CauchysMeanTheorem". (The well-know Cauchy's Mean Theorem says that the geometric mean is less than, or equal to, the arithmetic mean, for every finite collection of positive numbers. However, this theorem will appear much later, near the end of the source text.) The existing theory "Complex_Main" is a prerequisite. (It contains main facts about real and complex numbers; only real numbers are relevant, but some useful formulas about appear in "Complex_Main".)
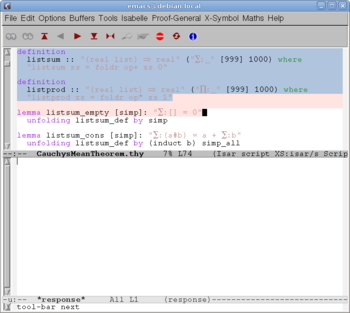
Clicking the red button "" we send the first portion of the text to Isabelle. After two more such clicks Isabelle reads the line "imports Complex_Main" and finds in the library the "Complex_Main" theory (since it is a prerequisite to the new "CauchysMeanTheorem"), but also "Real", since it appears to be a prerequisite to "Complex_Main", and so on, recursively, until all prerequisites are found and processed (in a logical order). Then, after 9 more clicks we come to the screen shown on Fig. 3. The definitions (and everything before them) are already processed by Isabelle; accordingly, they turn into blue, and become read-only. The formulation of the first lemma is being processed by Isabelle; accordingly, it turns into orange. A fraction of a second later we get Fig. 4. The formulation of the lemma is read by Isabelle; a dialog about its proof starts on the bottom window.
A robot as a student
The first lemma "listsum_empty" (of the new "CauchysMeanTheorem" theory) is ridiculously trivial; it claims that the sum of the empty collection of numbers is equal to zero! Here is an explanation of this disturbing situation.
A human student would not start to learn Cauchy's mean theorem
being unfamiliar with such notions as the sum and the product of n numbers. However, a robot (like Isabelle) is not a human. A robot never was in a kindergarten or elementary school. We cannot say to Isabelle: "Look, here is a sum of three numbers: 15+5+10=30; note that also 5+10+15=30 etc. Likewise, any finite collection of numbers has its sum." Children proceed from the particular to the general, but proof assistants proceed from the general to the particular.
For now, Isabelle is not well-educated. Its mathematical knowledge is rather fragmentary. Some volunteers contribute some theories to the library of Isabelle; this is not a well-organized process rich of resources. Each contributor has to find out, which of the relevant facts are already known to Isabelle and which are not.
Definitions of the sum and the product of a list of numbers are given to Isabelle just before the first lemma (see "listsum" and "listprod" on Fig. 3 or 4) in terms of
- addition and multiplication for two numbers (already known), and
- "foldr", the right fold operation defined in the "List" theory (one of the prerequisites).
Informally, the right fold applies to a binary operation (say, "+"), a list (say, "[x,y,z]") and an initial value (say, "a"), giving "x+(y+(z+a))"; more formally,
foldr op+ [x,y,z] a = x+(y+(z+a)).
(For the summation case one may write just "x+y+z+a", but in general an operation need not be associative.) The "listsum" definition stipulates the addition operation and the initial value 0; the "listprod" definition stipulates the multiplication operation and the initial value 1. The sum of a list is denoted by Isabelle as follows:
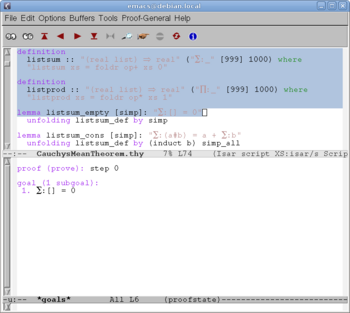
A human student, given by such a formal definition of sum (only sketched here) would not be too astonished by the trivial exercise "prove that the sum of the empty list is equal to 0"; this is our "listsum_empty" lemma. After the formulation, the source text contains a hint to the proof,
unfolding listsum_def by simp
which means informally: "Isabelle, use the definition of the sum of a list, do evident simplifications, and hopefully you'll find a proof of the lemma." And indeed, Isabelle is cute enough in order take the hint. After a fraction of a second it reports that the lemma is successfully proved.
Now we continue the example session.
Hard work
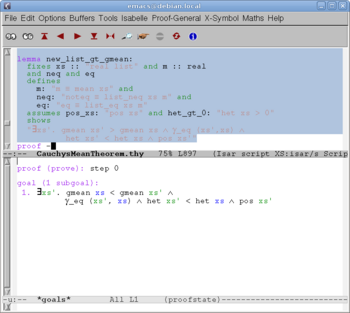
After more than 30 rather boring, mostly trivial lemmas, whose proofs vary in length from one line to about 50 lines, we arrive to a more interesting lemma (Fig. 5) and start proving it (Fig. 6).
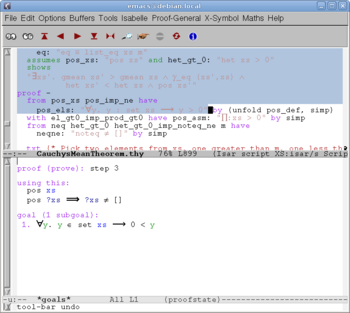
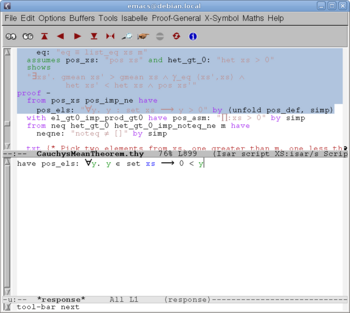
We make a claim of the form "from A have B..."; Isabelle responds by "using this: A, goal: B" (Fig. 7) and waits. We add a hint "...by C"; Isabelle takes the hint, finds a proof and responds by "have B" (Fig. 8).
We continue; the work becomes hard (Fig. 9). After a lot of effort we get close to the happy end (Fig. 10), and finally the theorem is proved (Fig. 11).
Options
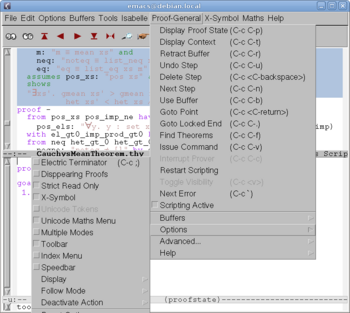
Many options are available for Proof General (Fig. 12) and Isabelle. In particular, many kinds of additional information may be requested from Isabelle at any moment of the session (Fig. 13).
Higher-order logic versus theory of sets
The logical structure of a mathematical text is "the choreography of and " [2]; these are symbols for quantifiers ("for all", "exists") and connectives ("and", "or", "implies"). Quantifiers bind variables; each variable runs over its domain.
Example 1. Every real number has its qubic root. More formally, for every real number x there exists a real number y such that . Symbolically, . Variables x, y run over the real line
Example 2. Every bounded set of real numbers has its least upper bound. More formally: for every subset A of the real line, if there exists a real x greater than, or equal to, all elements of A, then there exists the least such x. The variable A runs over the set of all subsets of the real line.
Example 3. Every continuous map (that is, function) from a circle to a sphere can be extended to a continuous map from the disk (bounded by the circle) to the sphere. Here, variables run over maps.
We observe that the domain of a variable is a given set X (first-order logic), or the set of all maps from one given set X to another given set Y (second-order logic), or a set that results from several given sets by a finite number of such operations (higher order logic). In particular, third-order logic appears when dealing with all topologies on X. Subsets of X may be treated as maps ; sequences of points of X may be treated as maps .
Using Isabelle/HOL syntax, Example 1 may be written as "x::real. y::real. ", which is of first order. Second-order examples: "for every subset A of the real line" may be written as "A::real set" while "for every function f from the real line to itself" may be written as "f::{real}real".
Example 4. Every linear space has a basis. Here, one variable runs over the class of all linear spaces, and another variable - over the set of all subsets of the linear space.
The class of all linear spaces cannot be treated as a (given) set. It may seem that we must leave the higher-order logic for the theory of sets. However, we may redesign the theory of linear spaces as a theory with the axiom "L is a linear space", and the theorem as "L has a basis". Now only one variable is used, and it runs over L. The quantifier "for every linear space L" becomes implicit; the theory holds for all linear spaces.
During the 20 century the theory of sets was used as a universal infrastructure behind various specialized mathematical theories. The higher-order logic is weaker than the theory of sets, but still strong enough in order to accommodate the specialized theories. For those preferring the habitual set-theoretic framework, Isabelle (combined with Isar and Proof General) provides the option to use the logic ZF (Zermelo-Frenkel theory of sets) instead of HOL (higher-order logic). This approach is used in IsarMathLib. Here is a quotation from "Questions and Answers of IsarMathLib" (see the external links page):
- Q3: Why ZF logic?
- A: Almost all mathematics I know about is based on the first order logic and Zermelo-Fraenkel set theory. This is what I was taught in high school and feels natural to me. I am sure other logical frameworks, like HOL, are interesting and useful, but someone would have to pay me money to make me twist my brain around HOL and its typed set theory.
Comparing IsarMathLib with the HOL library it is easy to note that HOL makes the formal text shorter, simpler, and more elegant (but of course, less habitual), while ZF leaves idle the helpful mechanism of types. In the long run this loss should outweigh the burden of initial learning again.
Reliability
Availability
Other systems
- Mizar
- Hol88, Hol98, Hol4, Hol Light
- Lego, Coq
- Lambda-CLAM
- Matita
- Otter
- Prover9
- Mace2
- Jape, Ssreflect, PhoX, pvs
- ACL2, Twelf
Notes
- ↑ Bourbaki 1968, page 8.
- ↑ Taylor p.44
References
Bourbaki, Nicolas (1968), Elements of mathematics: Theory of sets, Hermann (original), Addison-Wesley (translation).


![{\displaystyle {\sqrt[{n}]{a_{1}\dots a_{n}}}\leq {\frac {a_{1}+\dots +a_{n}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01331288193287c9f28c73bb42a21a974b73025d)


![{\displaystyle \Sigma :[x,y,z]=x+(y+(z+0))\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91df07687dea2b3c034e9bf48ad5b7fd5c354426)