Electric displacement: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 17: | Line 17: | ||
</math> | </math> | ||
where the symbol '''∇'''⋅ gives the [[divergence]] of '''D'''('''r''') and ρ('''r''') is the charge density at the point '''r'''. | where the symbol '''∇'''⋅ gives the [[divergence]] of '''D'''('''r''') and ρ('''r''') is the charge density at the point '''r'''. | ||
==Relation of D to surface charge density σ== | |||
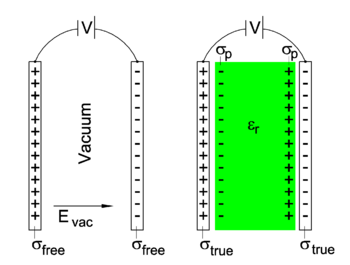
[[Image: Dielectric.png|thumb|right|350px|Two capacitors at same voltage ''V''. On the left vacuum between the plates and on the right a dielectric with relative permittivity ε<sub>r</sub>. Absolute values of surface charge densities are indicated by σ.]] | |||
The electric displacement ''D'' (is the magnitude of vector '''D''', which points from − to + charge) is equal to the true surface charge density σ<sub>true</sub> indicated in the figure, | |||
where two [[parallel-plate capacitor]]s are shown that are completely identical except for the matter between the plates. In particular the plates have the same voltage difference ''V''. | |||
To explain this interpretation of ''D'', we recall that the [[relative permittivity]] may be defined as the ratio of two [[capacitances]], ''C'' ≡ ''Q'' / ''V'', namely the ratio of the capacitance ''C'' of the capacitor filled with dielectric to the capacitance ''C''<sub>vac</sub> of a capacitor in vacuum, | |||
:<math> | |||
\epsilon_\mathrm{r} \equiv \frac{C}{C_\mathrm{vac}} = \frac{Q_\mathrm{true}}{V} \left[ \frac{Q_\mathrm{free}}{V}\right]^{-1} = | |||
\frac{Q_\mathrm{true}}{Q_\mathrm{free}} = \frac{\sigma_\mathrm{true}}{\sigma_\mathrm{free}}, | |||
</math> | |||
where we used that ''Q'' is σ × ''A'', with ''A'' the area of the plates. | |||
<!-- | <!-- | ||
The value of the electric displacement D may be thought of as equal to the amount of free charge on one plate divided by the area of the plate. From this point of view D is frequently called the electric flux density, or free charge surface density, because of the close relationship between electric flux and electric charge. The dimensions of electric displacement, or electric flux density, in the metre-kilogram-second system are charge per unit area, and the units are coulombs per square metre. In the centimetre-gram-second system the dimensions of D are the same as those of the primary electric field E, the units of which are dynes per electrostatic unit, or statvolts per centimetre. | The value of the electric displacement D may be thought of as equal to the amount of free charge on one plate divided by the area of the plate. From this point of view D is frequently called the electric flux density, or free charge surface density, because of the close relationship between electric flux and electric charge. The dimensions of electric displacement, or electric flux density, in the metre-kilogram-second system are charge per unit area, and the units are coulombs per square metre. In the centimetre-gram-second system the dimensions of D are the same as those of the primary electric field E, the units of which are dynes per electrostatic unit, or statvolts per centimetre. | ||
--> | --> | ||
==Tensor character of D== | |||
As defined here, '''D''' and '''E''' are proportional, i.e., ε<sub>r</sub> is a number (a scalar). For a ''non-isotropic'' dielectric ε<sub>r</sub> may be a second rank [[tensor]], | As defined here, '''D''' and '''E''' are proportional, i.e., ε<sub>r</sub> is a number (a scalar). For a ''non-isotropic'' dielectric ε<sub>r</sub> may be a second rank [[tensor]], | ||
:<math> | :<math> | ||
| Line 31: | Line 46: | ||
</math> | </math> | ||
--> | --> | ||
'''(To be continued)''' | '''(To be continued)''' | ||
Revision as of 05:07, 5 December 2008
In physics, electric displacement, usually denoted by D, is a vector field in a non-conducting medium, a dielectric, that is proportional to the electric field E. In SI units,
where ε0 is the electric constant and εr is the relative permittivity. In Gaussian units ε0 is not defined and may put equal to unity. In vacuum the dimensionless quantity εr = 1 (both for SI and Gaussian units) and D is simply related, or equal, to E. Often D is termed an auxiliary field with the principal field being E. An alternative auxiliary field is the electric polarization P of the dielectric,
The vector field P describes the polarization (displacement of charges) occurring in a dielectric when it is inserted between the charged plates of a parallel-plate capacitor. Clearly, the fact that for any insulator εr > 1 (i.e., that D is not simply equal to εrE) has the same physical origin.
The electric displacement appears in one of the macroscopic Maxwell equations,
where the symbol ∇⋅ gives the divergence of D(r) and ρ(r) is the charge density at the point r.
Relation of D to surface charge density σ
The electric displacement D (is the magnitude of vector D, which points from − to + charge) is equal to the true surface charge density σtrue indicated in the figure, where two parallel-plate capacitors are shown that are completely identical except for the matter between the plates. In particular the plates have the same voltage difference V.
To explain this interpretation of D, we recall that the relative permittivity may be defined as the ratio of two capacitances, C ≡ Q / V, namely the ratio of the capacitance C of the capacitor filled with dielectric to the capacitance Cvac of a capacitor in vacuum,
where we used that Q is σ × A, with A the area of the plates.
Tensor character of D
As defined here, D and E are proportional, i.e., εr is a number (a scalar). For a non-isotropic dielectric εr may be a second rank tensor,
(To be continued)



![{\displaystyle \epsilon _{\mathrm {r} }\equiv {\frac {C}{C_{\mathrm {vac} }}}={\frac {Q_{\mathrm {true} }}{V}}\left[{\frac {Q_{\mathrm {free} }}{V}}\right]^{-1}={\frac {Q_{\mathrm {true} }}{Q_{\mathrm {free} }}}={\frac {\sigma _{\mathrm {true} }}{\sigma _{\mathrm {free} }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c05bbde9cced290ddf8f2450ae50a16ccf68065d)
