Circle (mathematics): Difference between revisions
imported>Daniel Mietchen m (Circle moved to Circle (mathematics): disambig) |
imported>Donal O'Hara No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
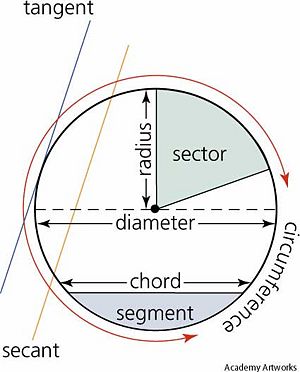
[[Image:A4circle.jpg|right|thumb|300px|Image of a circle showing the key labels]] | |||
A '''circle''' is most commonly a [[locus]] of [[Point (geometry)|points]] in a [[Plane (geometry)|plane]] equidistant from a single point, the center. The term may also refer to similarly defined loci on other two-dimensional [[Manifold (geometry)|manifolds]]. | |||
The circle has been of incredible interest to mathematicians since [[mathematics|mathematics']] foundation. The circle serves as the starting point for much of mathematics, for example '''[[pi|π]]''' was first encountered as the ratio of a circle's diameter to its circumference. | |||
The circle also serves as the starting point for the [[trigonometric function|tirgonometric functions]] sine, cosine and tan. The functions are dervied from the unit circle. As shown below, at any point on the circle's circumference the x coordinate is given by <math>\cos \theta \,</math>, the y coordinate is given by <math>\sin \theta \,</math> and the gradient of the radius for the centre (0,0) to the point (x,y) is given by <math>\tan \theta \,</math> where <math>\theta\,</math> is the angle between the radius and the x-axis.[[Image:unit_circle.gif|left|thumb|200px]] | |||
The circle is also one of the 4 [[conic section|conic sections]]. It is represented algebraically as <math>(x - a)^2 + (y - b)^2 = c^2</math> where the circle's centre is the point (a,b) and it has radius c. | |||
In the complex plane a circle is represented by the locus that satisfies the equation <math>(z - a) = b</math>; in this case the circle would have centre a and radius b. | |||
For a given circle of radius, r the Circumference = 2πr & the Area = πr<sup>2</sup> | |||
[[Category:Mathematics Workgroup]] | [[Category:Mathematics Workgroup]] | ||
[[Category:Stub Articles]] | [[Category:Stub Articles]] | ||
Revision as of 11:48, 3 July 2008
A circle is most commonly a locus of points in a plane equidistant from a single point, the center. The term may also refer to similarly defined loci on other two-dimensional manifolds.
The circle has been of incredible interest to mathematicians since mathematics' foundation. The circle serves as the starting point for much of mathematics, for example π was first encountered as the ratio of a circle's diameter to its circumference.
The circle also serves as the starting point for the tirgonometric functions sine, cosine and tan. The functions are dervied from the unit circle. As shown below, at any point on the circle's circumference the x coordinate is given by , the y coordinate is given by and the gradient of the radius for the centre (0,0) to the point (x,y) is given by where is the angle between the radius and the x-axis.
The circle is also one of the 4 conic sections. It is represented algebraically as where the circle's centre is the point (a,b) and it has radius c.
In the complex plane a circle is represented by the locus that satisfies the equation ; in this case the circle would have centre a and radius b.
For a given circle of radius, r the Circumference = 2πr & the Area = πr2