Plane (geometry)

Please create the "Talk page". Just click this Talk page link and save the page.

In Euclidean geometry, a plane is defined as a flat surface that for any two of its points entirely contains the straight line joining them. Until well into the nineteenth century it was thought that the only geometry possible was Euclidean and consequently this definition of "plane" was considered satisfactory. However, with the birth of non-Euclidean geometry and attention to the logical foundations of mathematics in the second half of the nineteenth century, doubts arose about the exactness and the limitations of the Euclidean definition of a plane.

In 1899 David Hilbert published his seminal book Grundlagen der Geometrie [Foundations of Geometry] in which he re-investigated and rephrased Euclid's two-millennia-old axioms and propositions. Hilbert begins with listing undefined concepts, among which are "point", "line", and "plane". In terms of these undefined concepts Hilbert formulates sets of axioms. The first axiom regarding the plane is axiom I4: Three points A, B, C that are not on one and the same line determine always a plane α. He adds that this is expressed as "A, B, and C lie in α", or "A, B, and C are points of α". His axiom I5 is a subtle extension of I4: Any three points in plane α that are not on one line determine plane α.

This article discusses some possible geometrical definitions of a plane as a locus of points and mentions its modern definition as two-dimensional subspace of an affine space.

(CC) Image: Dina Tsirelson
The surface of this metallic body consists of rectangles situated in various planes.

Non-axiomatic approach

Definitions

A remark

To define a plane is more complicated than it may seem.

It is tempting to define a plane as a surface with zero curvature (or something like that). However, this is not a good idea, since the notions of surface and curvature are much more complicated than the notion of plane. In fact, several different notions of surface are introduced by topology and differential geometry, and several different notions of curvature are introduced by differential geometry; these are far beyond elementary mathematics. Fortunately, it is possible to define a plane via more elementary notions, and this way is preferred in mathematics. Still, the definitions given below are tentative. They are criticized afterwards, see axiomatic approach.

The definitions of "plane" given below may be compared with the definition of a circle as consisting of those points in a plane that are a given distance (the radius) away from a given point (the center). A circle is a set of points chosen according to their relation to some given parameters (center and radius). Similarly, a plane is a set of points chosen according to their relation to some given objects (points, lines etc). However, a circle determines its center and radius uniquely; for a plane, the situation is different.

Four equivalent definitions of "plane" are given below. Any other definition is equally acceptable provided that it is equivalent to these. Note that a part of a plane is not a plane. Likewise, a line segment is not a line.

Below, all points, lines and planes are situated in the space (assumed to be a three-dimensional Euclidean space), and by lines we mean straight lines.

Definition via distances

Let two different points A and B be given. The set of all points C that are equally far from A and B — that is,

$|AC|=|BC|$

— is a plane.

This is the plane orthogonal to the line AB through the middle point of the line segment AB.

Definition via right angles (orthogonality)

Let two different points A and B be given. The set of all points C such that the lines AB and AC are orthogonal (that is, the angle BAC is right) is a plane.

This is the plane orthogonal to the line AB through the point A.

Every point F on the line DE belongs to the plane through given points A, B and C, provided that D belongs to AB, E belongs to BC, and D, E do not coincide with B.

Definition via lines

Let three points A, B and C be given, not lying on a line. Consider the lines DE for all points D on the line AB different from B and all points E on the line BC different from B. The union of all these lines, together with the point B, is a plane.

This is the plane through A, B and C.

In other words, this plane is the set of all points F such that either F coincides with B or there exists a line through F that intersects both the line AB and the line BC, and not at their intersection point B.

Definition via Cartesian coordinates

In terms of Cartesian coordinates x, y, z ascribed to every point of the space, a plane is the set of points whose coordinates satisfy the linear equation ax+by+cz=d. Here real numbers a, b, c and d are parameters such that at least one of a, b, c does not vanish.

Some properties of planes

Most basic properties

For any three points not situated in the same straight line there exists one and only one plane that contains these three points.

If two points of a straight line lie in a plane, then every point of the line lies in that plane.

If two planes have a common point then they have at least a second point in common.

Every plane contains at least three points not lying in the same straight line, and the space contains at least four points not lying in a plane.

Further properties

Two planes either do not intersect (are parallel), or intersect in a line, or coincide.

A line either does not intersect a plane (is parallel to it), or intersects it in a single point, or is contained in the plane.

Two lines perpendicular to the same plane are parallel to each other (or coincide).

Two planes perpendicular to the same line are parallel to each other (or coincide).

Axiomatic approach

What is wrong with the definitions given above?

The definitions given above assume implicitly that the 3-dimensional Euclidean space is already defined, together with (at least one of) such notions as distances, angles, straight lines, Cartesian coordinates, while planes are not defined yet. However, this situation never appears in mathematical theory.

In the axiomatic approach points, lines and planes are undefined primitives.

The modern approach (below) defines planes in a completely different way.

How does it work

Axiomatic approach is similar to chess in the following aspect.

A chess piece, say a rook, cannot be defined before the whole chess game is defined, since such a phrase as "the rook moves horizontally or vertically, forward or back, through any number of unoccupied squares" makes no sense unless it is already known that "chess is played on a square board of eight rows and eight columns" etc. And conversely, the whole chess game cannot be defined before each piece is defined; the properties of the rook are an indispensable part of the rules of the game. No chess without rooks, no rooks outside chess! One must introduce the game, its pieces and their properties in a single combined definition.

Likewise, Euclidean space, its points, lines, planes and their properties are introduced simultaneously in a set of 20 assumptions known as Hilbert's axioms of Euclidean geometry. The "most basic properties of planes" listed above are roughly the plane-related assumptions (Hilbert's axioms), while "further properties" are the first plane-related consequences (theorems).

Modern approach

The modern approach defines the three-dimensional Euclidean space more algebraically, via linear spaces and quadratic forms, namely, as a real affine space whose difference space is a three-dimensional inner product space. For further details see Affine space#Euclidean space and space (mathematics).

In this approach a plane in an n-dimensional affine space (n ≥ 2) is defined as a (proper or improper) two-dimensional affine subspace.

A less formal version of this approach uses points, vectors and scalar product (called also dot product or inner product) of vectors without mentioning linear and affine spaces. Optionally, Cartesian coordinates of points and vectors are used. See algebraic equations below. There, in particular, equivalence between the definition via right angles (orthogonality) and the definition via Cartesian coordinates is explained.

Plane geometry

Plane geometry (also called "planar geometry") is a part of solid geometry that restricts itself to a single plane ("the plane") treated as a geometric universe. In other words, plane geometry is the theory of the two-dimensional Euclidean space, while solid geometry is the theory of the three-dimensional Euclidean space.

A plane figure is a combination of points and/or lines that fall on the same plane. In plane geometry every figure is plane, in contrast to solid geometry.

A rectilinear figure is a plane figure consisting of points, straight lines and straight line segments only. Rectilinear figures include triangles and polygons.

Algebraic equations

In analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. A few algebraic representations will be discussed.

Point-normal representation

PD Image
Fig. 1. Equation for plane. P is arbitary point in plane; $\scriptstyle {\vec {d}}$ and $\scriptstyle {\vec {n}}_{0}$ are collinear.

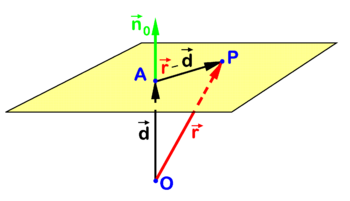
One such equation is illustrated in figure 1. Point P is an arbitrary point in the plane and O (the origin) is drawn outside the plane, but may also be in the plane. The point A in the plane is chosen such that vector

${\vec {d}}\equiv {\overrightarrow {OA}}$

is orthogonal to the plane. The collinear vector

${\vec {n}}_{0}\equiv {\frac {1}{d}}{\vec {d}}\quad {\hbox{with}}\quad d\equiv \left|{\vec {d}}\,\right|$

is a unit (length 1) vector normal (perpendicular) to the plane which is known as the normal of the plane in point A. Note that d is the distance of O to the plane. The following relation holds for an arbitrary point P in the plane

$\left({\vec {r}}-{\vec {d}}\;\right)\cdot {\vec {n}}_{0}=0\quad {\hbox{with}}\quad {\vec {r}}\equiv {\overrightarrow {OP}}\quad {\hbox{and}}\quad {\vec {r}}-{\vec {d}}={\overrightarrow {AP}}.$

This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows for component vectors (real triplets) that are written bold, we find

$\left(\mathbf {r} -\mathbf {d} \right)\cdot \mathbf {n} _{0}=0\Longleftrightarrow xa_{0}+yb_{0}+zc_{0}=d$

with

$\mathbf {d} =(a,\;b,\;c),\quad \mathbf {n} _{0}=(a_{0},\;b_{0},\;c_{0}),\quad \mathbf {r} =(x,\;y,\;z),$

and

$\mathbf {d} \cdot \mathbf {n} _{0}={\frac {1}{d}}\mathbf {d} \cdot \mathbf {d} =d={\sqrt {a^{2}+b^{2}+c^{2}}}.$

From this follows the Hesse normal form for the plane (called after the 19th century mathematician Ludwig Otto Hesse):

$\mathbf {r} \cdot \mathbf {n} _{0}=d.$

Conversely, given the following equation for a plane

$ax+by+cz=e,\,$

it is easy to derive the same equation. Write

$\mathbf {r} =(x,\;y,\;z),\quad \mathbf {f} =(a,\;b,\;c),\quad {\hbox{and}}\quad \mathbf {d} \equiv \left({\frac {e}{a^{2}+b^{2}+c^{2}}}\right)\mathbf {f} .$

It follows that

$\mathbf {f} \cdot \mathbf {r} =e=\mathbf {f} \cdot \mathbf {d} .$

Hence we find the same equation,

$\mathbf {f} \cdot (\mathbf {r} -\mathbf {d} )=0\;\Longrightarrow \;(\mathbf {r} -\mathbf {d} )\cdot \mathbf {n} _{0}=0\quad {\hbox{with}}\quad \mathbf {n} _{0}={\frac {1}{\sqrt {a^{2}+b^{2}+c^{2}}}}\mathbf {f}$

where f , d, and n₀ are collinear. The equation may also be written in the following mnemonically convenient form

$\mathbf {d} \cdot (\mathbf {r} -\mathbf {d} )=0,$

which is the equation for a plane through a point A perpendicular to ${\overrightarrow {OA}}={\vec {d}}$.

Three-point representation

PD Image
Fig. 2. Plane through points A, B, and C.

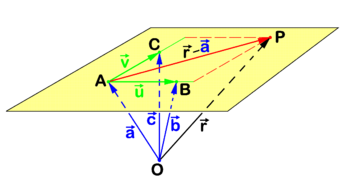
Figure 2 shows a plane that by definition passes through three different points A, B, and C that are not on one line. The point P is an arbitrary point in the plane and the reference point O is again drawn outside the plane, but the case that the plane passes through O is not excluded. Referring to figure 2 we introduce the following definitions

${\vec {a}}={\overrightarrow {OA}},\quad {\vec {b}}={\overrightarrow {OB}},\quad {\vec {c}}={\overrightarrow {OC}},\quad {\vec {r}}={\overrightarrow {OP}}.$

Clearly the following two non-collinear vectors belong to the plane

${\vec {u}}={\overrightarrow {AB}}={\vec {b}}-{\vec {a}},\quad {\vec {v}}={\overrightarrow {AC}}={\vec {c}}-{\vec {a}}.$

Because a plane (an affine space), with a given fixed point as origin is a 2-dimensional linear space and two non-collinear vectors with "tails" in the origin are linearly independent, it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors (this is also expressed as: any vector in the plane can be decomposed into components along the two non-collinear vectors). In particular, taking A as origin in the plane,

${\overrightarrow {AP}}={\vec {r}}-{\vec {a}}=\lambda {\vec {u}}+\mu {\vec {v}},\qquad \lambda ,\mu \in \mathbb {R} .$

The real numbers λ and μ specify the direction of ${\overrightarrow {AP}}$. Hence the following equation for the position vector ${\vec {r}}$ of the arbitrary point P in the plane:

${\vec {r}}={\vec {a}}+\lambda {\vec {u}}+\mu {\vec {v}}$

is known as the point-direction representation of the plane. This representation is equal to the three-point representation

${\vec {r}}={\vec {a}}+\lambda ({\vec {b}}-{\vec {a}})+\mu ({\vec {c}}-{\vec {a}}),$

where ${\vec {a}}$, ${\vec {b}}$, and ${\vec {c}}$ are the position vectors of the three points that define the plane.

Writing for the position vector of the arbitrary point P in the plane

${\vec {r}}=(1-\lambda -\mu )\,{\vec {a}}+\lambda \,{\vec {b}}+\mu \,{\vec {c}}\;\equiv \;\xi _{1}\,{\vec {a}}+\xi _{2}\,{\vec {b}}+\xi _{3}\,{\vec {c}}\;,$

we find that the real triplet (ξ₁, ξ₂, ξ₃) with ξ₁ + ξ₁ + ξ₁ = 1 forms a set of coordinates for P. The numbers {ξ₁, ξ₂, ξ₃ | ξ₁+ ξ₂+ ξ₃ = 1 } are known as the barycentric coordinates of P. It is trivial to go from barycentric coordinates to the "three-point representation",

${\vec {r}}=\xi _{1}{\vec {a}}+\xi _{2}{\vec {b}}+\xi _{3}{\vec {c}}\quad {\hbox{with}}\quad \xi _{1}=1-\xi _{2}-\xi _{3}\;\Longleftrightarrow \;{\vec {r}}={\vec {a}}+\xi _{2}({\vec {b}}-{\vec {a}})+\xi _{3}({\vec {c}}-{\vec {a}}).$

Beyond mathematics

In industry, a surface plate is a piece of cast iron or other appropriate material whose surface (or rather a part of it) is made as close as possible to a geometric plane. An old method of their manufacturing is the three-plate method: three roughly flat surfaces become more and more flat when rubbing against each other: first and second; second and third; third and first; first and second again, and so on. It is possible to achieve a surface close to a plane up to 10^–5 of its size.