Metre (unit): Difference between revisions
imported>John R. Brews |
imported>John R. Brews mNo edit summary |
||
| Line 91: | Line 91: | ||
Another small dimension technique is the [[atomic force microscope]]. Calibration is attempted using standard samples measured by [[Transmission electron microscope|transmission electron microscopy]].<ref name=Orji> | Another small dimension technique is the [[atomic force microscope]]. Calibration is attempted using standard samples measured by [[Transmission electron microscope|transmission electron microscopy]].<ref name=Orji> | ||
{{cite journal |title=TEM calibration methods for critical dimension standards |author=NG Orji ''et al.'' |url=ftp://129.6.13.25/pub/eeel/cresswell/orji_spie_2007.pdf |year=2007 |journal Proc. of SPIE |volume=vol. 6518 |doi=10.1117/12.713368}} | {{cite journal |title=TEM calibration methods for critical dimension standards |author=NG Orji ''et al.'' |url=ftp://129.6.13.25/pub/eeel/cresswell/orji_spie_2007.pdf |year=2007 |journal= Proc. of SPIE |volume=vol. 6518 |doi=10.1117/12.713368}} | ||
</ref> | </ref> | ||
Revision as of 12:16, 7 April 2011
The metre (American meter) is the basic unit of length measurement in the International System of Units (SI) commonly known as the metric system. The metre is abbreviated as m, appearing after the quantity.
Currently, the SI units define the metre in terms of the speed of light and the second, such that the metre is the length traveled by light in the reference medium of classical vacuum in the time interval of 1/299 792 458 second.[1][2] The metre has been adopted as the fundamental unit of length in almost all countries of the world, with the United States being a notable exception.
An easily realized and reproducible measurement is a major goal of metrology. The practicality of adoption of a time of flight as a measure of length depends critically upon the experimental fact that the speed of light in vacuum is a universal constant to within experimental error. As a result of the present definition, aside from the error in measuring transit times, length measurements are subject only to the uncertainty in relating the medium used in a particular measurement to a reference vacuum, taken in SI units to be the classical vacuum.
The metre is also the basis of the SI units of area and volume, which are the square metre (m2) and cubic metre (m3), respectively.
Very few adult humans are as tall as 2m in height.
History
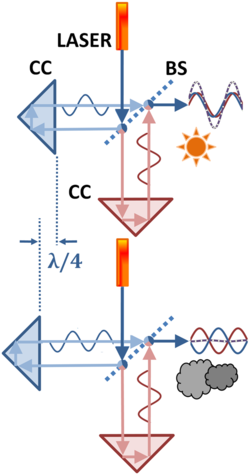
Measuring a length in wavelengths of light using a Michelson interferometer.
The metre was initially adopted as a unit of measure in France in 1790, during the French Revolution.
The original definition of the metre was the length of a pendulum with a half-period of 1 second, but was changed in 1791 to be the length of a prototype bar which was supposed to be 1/10 000 000 of the length of the meridian of Paris from the north pole to the equator. Since then, the metre has been redefined a number of times.[3]
After 1960 and before the switch to the transit-time definition in 1983, lengths were measured in terms of the number of wavelengths of light that could be fitted into them. The figure shows schematically how length was determined: the two panels show a laser source emitting a light beam split to travel two paths by a beam splitter (BS). The light is recombined by bouncing the two components off a pair of corner cubes (CC) that return the two components to the beam splitter again to be reassembled. The distance between the left-hand corner cube and the beam splitter is compared to that separation on the fixed leg as the left-hand spacing is adjusted to match the length of the object to be measured.[4]
In the top panel the path is such that the two beams reinforce each other after reassembly, leading to a strong light pattern (sun). The bottom panel shows a path that is made a half wavelength longer by moving the left-hand mirror a quarter wavelength further away, increasing the path difference by a half wavelength. The result is the two beams are in opposition to each other at reassembly, and the recombined light intensity drops to zero (clouds). Thus, as the spacing between the mirrors is adjusted, the observed light intensity cycles between reinforcement and cancellation as the number of wavelengths of path difference changes, and the observed intensity alternately peaks (sun) and dims (clouds). This behavior is called interference and the machine is called an interferometer. By counting fringes it is found how many wavelengths long the measured path is compared to the fixed leg.
This methodology for length determination requires a careful specification of the wavelength of the light used, and is one reason for employing a laser source. The precise definition of the metre was established in the 11th CGPM of 1960 as 1 650 763.73 wavelengths of the 2p10−5d5 line of krypton-86.[5] The measurement also requires careful specification of the medium in which the light propagates, which must be related to a reference medium of ideal vacuum.
This interferometer methodology had an experimental uncertainty related to determining the precise frequency of the source[6] and the careful measuring of the interference pattern that led in 1983 (along with other considerations spelled out in the final decision) to the switch to the more exact procedure based upon the transit time of light.[1]
Small dimensions
Measurements of the dimension of small objects is not done using transit time measurements. Measurements are made in units of wavelengths λ at a known frequency f, and related to the metre using λ = c0 / f. For instance, in the case of a crystal, atomic spacings can be determined using X-ray diffraction.[7] The present best value for the lattice parameter of silicon, denoted a, is:[8]
- a = 543.102 064(14) × 10−12 m.
Similar techniques can provide the dimensions of small structures repeated in large periodic arrays like a diffraction grating.[9]
Measuring dimensions of localized structures (as opposed to large arrays of atoms like a crystal) is more difficult. For example, dimensions in tens of nm in modern integrated circuits are observed using the scanning electron microscope. This instrument bounces electrons off the object to be measured in a high vacuum enclosure, and the reflected electrons are collected as a photodetector image that is interpreted by a computer. These are not transit time measurements, but are based upon comparison of Fourier transforms of images with theoretical results from computer modeling. Such elaborate methods are required because the image depends on the three-dimensional geometry of the measured feature, for example, the contour of an edge, and not just upon one- or two-dimensional properties. The underlying limitations are the beam width and the wavelength of the electron beam (determining diffraction), related to metres using λ = c0 / f, where the frequency is related to the electron beam energy.[10] The calibration of such measurements is tricky, as results depend upon the material measured and its geometry. A typical wavelength is 0.5 Å, and a typical resolution is about 4 nm.
Another small dimension technique is the atomic force microscope. Calibration is attempted using standard samples measured by transmission electron microscopy.[11]
Other systems of units
In some systems of units, unlike the current SI system, lengths are fundamental units (for example, wavelengths in the older SI units and bohrs in atomic units) and are not defined by times of transit. Even in such units, however, the comparison of two macroscopic lengths can be made more accurately by comparing the two transit times of light along the lengths. Using present techniques, a transit time often is more accurately measured than is the determination of a length as a multiple of the fundamental length unit.
Traditional units
The foot has been defined in the United States to equal exactly 0.3048m, though an earlier definition of the survey foot was 1200/3937 m, which is different than the current definition by about one part in 500 000. The inch, being 1/12 foot, is exactly 0.0254m, or 2.54cm.
The modern Chinese chǐ (市尺), or "Chinese foot", has been defined to equal exactly one-third of a meter. The Hong Kong chek (尺) is exactly 0.371475m. The Japanese kanejaku (曲尺) was defined as 10/33m in 1891.
The Spanish vara was fixed at about 835.9mm in 1801; however, the vara was defined in California as 838.2mm (33 inches), and in Texas as 846.666...mm (33 1/3 inches).
The megalithic yard is approximately 0.83m.
References
- ↑ 1.0 1.1 Resolution 1 of the 17th meeting of the Conférence Générale des Poids et Mesures (CGPM) (1983). 1983 definition of the metre. International Bureau of Weights and Measures (BIPM). Retrieved on 2011-03-19.
- ↑ The classical vacuum as a reference medium is described in Werner S. Weiglhofer and Akhlesh Lakhtakia (2003). “§ 4.1 The classical vacuum as reference medium”, Introduction to complex mediums for optics and electromagnetics. SPIE Press, 28, 34, 65. ISBN 9780819449474. and Tom G. MacKay (2008). “Electromagnetic Fields in Linear Bianisotropic Mediums”, Emil Wolf: Progress in Optics, Volume 51. Elsevier. ISBN 9780444520388.
- ↑ For a brief history, see Historical context of the SI. The NIST reference on constants, units and uncertainty. NIST. Retrieved on 2011-03-08.
- ↑ The corner cube reflects the incident light in a parallel path that is displaced from the beam incident upon the corner cube. That separation of incident and reflected beams reduces some technical difficulties introduced when the incident and reflected beams are on top of each other. For a discussion of this version of the Michelson interferometer and other types of interferometer, see Joseph Shamir (1999). “§8.7 Using corner cubes”, Optical systems and processes. SPIE Press, pp. 176 ff. ISBN 0819432261.
- ↑ Resolution 6 of the 11th meeting of the CGPM (1960). 1960 definition of the metre. International Bureau of Weights and Measures (BIPM). Retrieved on 2011-03-19.
- ↑ An atomic transition is affected by disturbances, such as collisions with other atoms, leading to a range of frequencies for the transition referred to as a linewidth. Corresponding to the uncertainty in frequency is an uncertainty in wavelength. In contrast, the speed of light in ideal vacuum is not dependent upon frequency at all.
- ↑ Peter J. Mohr, Barry N. Taylor, David B. Newell (2008). "CODATA recommended values of the fundamental physical constants: 2006". Rev Mod Phys vol. 80: pp. 633-730. See section 8: Measurements involving silicon crystals, p. 46.
- ↑ Lattice parameter of silicon. The NIST reference on constants, units and uncertainty. National Institute of Standards and Technology. Retrieved on 2011-04-04.
- ↑ A discussion of various types of gratings is found in Abdul Al-Azzawi (2006). “§3.2 Diffraction gratings”, Physical optics: principles and practices. CRC Press, pp. 46 ff. ISBN 0849382971.
- ↑ Michael T. Postek (2005). “Photomask critical dimension metrology in the scanning electron microscope”, Syed Rizvi: Handbook of photomask manufacturing technology. CRC Press, pp. 457 ff. ISBN 0824753747. and Harry J. Levinson (2005). “Chapter 9: Metrology”, Principles of lithography, 2nd ed. SPIE Press, pp. 313 ff. ISBN 0819456608.
- ↑ NG Orji et al. (2007). "TEM calibration methods for critical dimension standards". Proc. of SPIE vol. 6518. DOI:10.1117/12.713368. Research Blogging.