User:John R. Brews/WP Import: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>John R. Brews
No edit summary
 
(37 intermediate revisions by one other user not shown)
Line 1: Line 1:
{{AccountNotLive}}
{{TOC|right}}
{{TOC|right}}
In [[electronics]], the '''Miller effect''' accounts for the increase in the equivalent input [[capacitance]] of an inverting voltage [[amplifier]] due to amplification of the capacitance between the input and output terminals. The additional input capacitance due to the Miller effect is given by
[[Image:Current division example.svg|thumbnail|250px|Figure 1: Schematic of an electrical circuit illustrating current division. Notation ''R<sub>T<sub>.</sub></sub>''  refers to the ''total'' resistance of the circuit to the right of resistor ''R<sub>X</sub>''.]]
:<math>C_{M}=C (1-A_v)\ ,</math>
where ''A<sub>v</sub>''  is the voltage gain of the amplifier, which is a negative number because it is ''inverting'', and ''C'' is the feedback capacitance.


Although the term ''Miller effect'' normally refers to capacitance, the amplifier input impedance is modified by the Miller effect by any impedance connected between the input and another node exhibiting gain. These properties of the Miller effect are generalized in '''Miller's theorem'''.
In [[electronics]], a '''current divider ''' is a simple [[linear]] [[Electrical network|circuit]] that produces an output [[Electric current|current]] (''I''<sub>X</sub>) that is a fraction of its input current (''I''<sub>T</sub>). The splitting of current between the branches of the divider is called '''current division'''. The currents in the various branches of such a circuit divide in such a way as to minimize the total energy expended.


== History ==
The formula describing a current divider is similar in form to that for the [[voltage divider]]. However, the ratio describing current division places the impedance of the unconsidered branches in the [[numerator]], unlike voltage division where the considered impedance is in the numerator. To be specific, if two or more [[Electrical impedance|impedance]]s are in parallel, the current that enters the combination will be split between them in inverse proportion to their impedances (according to [[Ohm's law]]). It also follows that if the impedances have the same value the current is split equally.
The Miller effect was named after [[John Milton Miller]].<ref name=Miller/> When Miller published his work in 1920, he was working on [[vacuum tube]] triodes, however the same theory applies to more modern devices such as bipolar and MOS [[transistors]].


== Derivation ==
==Resistive divider==
{{Image|Miller effect.PNG|right|350px|Miller's theorem}}
A general formula for the current ''I<sub>X</sub>'' in a resistor ''R<sub>X</sub>'' that is in parallel with a combination of other resistors of total resistance ''R<sub>T</sub>'' is (see Figure 1): 
Consider a voltage [[amplifier]] of gain −''A'' with an [[Electrical impedance|impedance]] ''Z<sub>&mu;</sub>'' connected between its input and output stages. The input signal is provided by a [[Thévenin's theorem|Thévenin voltage source]] representing the driving stage. The voltage at the input end (node 1) of the coupling impedance is ''v<sub>1</sub>'', and at the output end  −''Av<sub>1</sub>''. The current through ''Z<sub>&mu;</sub>'' according to [[Ohm's law]] is given by:
:<math>I_X = \frac{R_T}{R_X+R_T}I_T \ </math>
where ''I<sub>T</sub>'' is the total current entering the combined network of ''R<sub>X</sub>'' in parallel with ''R<sub>T</sub>''. Notice that when ''R<sub>T</sub>'' is composed of a [[Series_and_parallel_circuits#Parallel_circuits|parallel combination]] of resistors, say ''R<sub>1</sub>'', ''R<sub>2</sub>'', ... ''etc.'', then the reciprocal of each resistor must be added to find the total resistance ''R<sub>T</sub>'':
:<math> \frac {1}{R_T} = \frac {1} {R_1} + \frac {1} {R_2} + \frac {1}{R_3} + ... \ . </math>


:<math>i_Z =   \frac{v_1 - (- A)v_1}{Z_\mu} = \frac{v_1}{ Z_\mu / (1+A)}</math>.
==General case==
Although the resistive divider is most common, the current divider may be made of frequency dependent [[Electrical impedance|impedance]]s. In the general case the current I<sub>X</sub> is given by:
:<math>I_X = \frac{Z_T} {Z_X+Z_T}I_T \ ,</math>


The input current is:
==Using Admittance==
Instead of using [[Electrical impedance|impedance]]s, the current divider rule can be applied just like the [[voltage divider]] rule if [[admittance]] (the inverse of impedance) is used.
:<math>I_X = \frac{Y_X} {Y_{Total}}I_T</math>
Take care to note that Y<sub>Total</sub> is a straightforward addition, not the sum of the inverses inverted (as you would do for a standard parallel resistive network). For Figure 1, the current I<sub>X</sub> would be
:<math>I_X = \frac{Y_X} {Y_{Total}}I_T = \frac{\frac{1}{R_X}} {\frac{1}{R_X} + \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}I_T</math>


:<math>i_1 = i_Z+\frac{v_1}{Z_{11}} \ . </math>
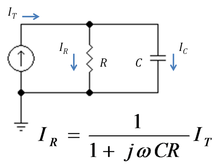
===Example: RC combination===
[[Image:Low pass RC filter.PNG|thumbnail|220px|Figure 2: A low pass RC current divider]]
Figure 2 shows a simple current divider made up of a [[capacitor]] and a resistor. Using the formula above, the current in the resistor is given by:


The impedance of the circuit at node 1 is:
::<math> I_R = \frac {\frac{1}{j \omega C}} {R + \frac{1}{j \omega C} }I_T </math>
:::<math> = \frac {1} {1+j \omega CR} I_T  \ , </math>
where ''Z<sub>C</sub> = 1/(jωC) '' is the impedance of the capacitor.


:<math>\frac {1}{Z_{1}} = \frac {i_1} {v_1} = \frac {1+A}{Z_\mu} +\frac{1}{Z_{11}} .</math>
The product ''τ = CR'' is known as the [[time constant]] of the circuit, and the frequency for which ωCR = 1 is called the [[corner frequency]] of the circuit. Because the capacitor has zero impedance at high frequencies and infinite impedance at low frequencies, the current in the resistor remains at its DC value ''I<sub>T</sub>'' for frequencies up to the corner frequency, whereupon it drops toward zero for higher frequencies as the capacitor effectively [[short-circuit]]s the resistor. In other words, the current divider is a [[low pass filter]] for current in the resistor.


This same input impedance is found if the input stage simply is decoupled from the output stage, and the lower impedance ''{{nowrap|Z<sub>&mu;</sub> / (1+A)}}'' is connected in parallel with ''Z<sub>11</sub>''. Of course, if the input stage is decoupled, no current reaches the output stage. To fix that problem, a dependent current source is attached to the second stage to provide the correct current to the output circuit, as shown in the lower figure. This decoupling scenario is the basis for '''Miller's theorem''' and the very noticeable prediction that the input impedance is reduced by the coupling between stages in the amount of the reduced impedance ''{{nowrap|Z<sub>&mu;</sub> / (1+A)}}'' shunted across the input is called the '''Miller effect'''.
==Loading effect==
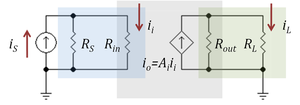
[[Image:Current division.PNG|thumbnail|300px|Figure 3: A current amplifier (gray box) driven by a Norton source (''i<sub>S</sub>'', ''R<sub>S</sub>'') and with a resistor load ''R<sub>L</sub>''. Current divider in blue box at input (''R<sub>S</sub>'',''R<sub>in</sub>'') reduces the current gain, as does the current divider in green box at the output (''R<sub>out</sub>'',''R<sub>L</sub>'')]]
The gain of an amplifier generally depends on its source and load terminations. Current amplifiers and transconductance amplifiers are characterized by a short-circuit output condition, and current amplifiers and transresistance amplifiers are characterized using ideal infinite impedance current sources. When an amplifier is terminated by a finite, non-zero termination, and/or driven by a non-ideal source, the effective gain is reduced due to the '''loading effect''' at the output and/or the input, which can be understood in terms of current division.  


== Effects ==
Figure 3 shows a current amplifier example. The amplifier (gray box) has input resistance ''R<sub>in</sub>'' and output resistance ''R<sub>out</sub>'' and an ideal current gain ''A<sub>i</sub>''. With an ideal current driver (infinite Norton resistance) all the source current ''i<sub>S</sub>'' becomes input current to the amplifier. However, for a [[Norton's theorem|Norton driver]] a current divider is formed at the input that reduces the input current to


The Miller effect shows up prominently in amplifier design, where the coupling impedance is a parasitic capacitance. If ''Z<sub>&mu;</sub>'' represents a capacitor with impedance ''Z<sub>&mu;</sub> = 1/j&omega;C<sub>&mu;</sub>'', the resulting input impedance has a huge capacitance ''(1+A)C<sub>&mu;</sub>'' attached in parallel with the nominal input impedance ''Z<sub>11</sub>''. This gain-enhanced capacitance is called the '''Miller capacitance''', ''C<sub>M</sub>'':
::<math>i_{i} = \frac {R_S} {R_S+R_{in}} i_S \ , </math>


:<math> C_{M}=C_\mu (1+A).</math>
which clearly is less than ''i<sub>S</sub>''. Likewise, for a short circuit at the output, the amplifier delivers an output current ''i<sub>o</sub>'' = ''A<sub>i</sub> i<sub>i</sub>'' to the short-circuit. However, when the load is a non-zero resistor ''R<sub>L</sub>'', the current delivered to the load is reduced by current division to the value:


That is, the effective or '''Miller capacitance''' ''C<sub>M</sub>'' is the physical ''C<sub>&mu;</sub>'' multiplied by the factor ''(1+A)''.<ref name=Spencer/> This huge capacitance seriously degrades the amplifier frequency performance, because this capacitance becomes a short-circuit at high frequencies, effectively preventing any signal from entering the amplifier. The bigger this Miller capacitance, the lower the frequency at which the amplifier fails to work.
::<math>i_L = \frac {R_{out}} {R_{out}+R_{L}} A_i  i_{i} \ . </math>


To illustrate this point, suppose ''Z<sub>11</sub> = R<sub>11</sub>'' and ''Z<sub>Th</sub> = R<sub>Th</sub>'', simple resistors. Application of [[Kirchhoff's current law]] at node 1 leads to the result:
Combining these results, the ideal current gain ''A<sub>i</sub>'' realized with an ideal driver and a short-circuit load is reduced to the '''loaded gain''' ''A<sub>loaded</sub>'':


:<math>\frac{v_1}{v_{Th}} = \frac{(R_{11}//R_{Th}}{R_{Th})}\ \frac{1}{1+j\omega (1+A)C_\mu (R_{11}//R_{Th})} \ , </math>
::<math>A_{loaded} =\frac {i_L} {i_S} = \frac {R_S} {R_S+R_{in}}</math> <math> \frac {R_{out}} {R_{out}+R_{L}} A_i  \ . </math>


which displays a roll-off of the input signal amplitude ''v<sub>1</sub>'' exciting the output stage for frequencies larger than:
The resistor ratios in the above expression are called the '''loading factors'''. For more discussion of loading in other amplifier types, see [[Voltage division#Loading effect|loading effect]].


:<math> \omega= \omega_C = \frac{1}{(1+A)C_\mu (R_{11}//R_{Th})} =   \frac{1}{C_M (R_{11}//R_{Th})} \ , </math>
===Unilateral versus bilateral amplifiers===
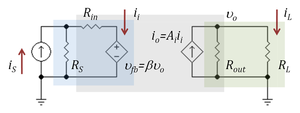
[[Image:H-parameter current amplifier.PNG|thumbnail|300px|Figure 4: Current amplifier as a bilateral two-port network; feedback through dependent voltage source of gain β V/V]]
Figure 3 and the associated discussion refers to a [[Electronic amplifier#Unilateral or bilateral|unilateral]] amplifier. In a more general case where the amplifier is represented by a [[two-port network|two port]], the input resistance of the amplifier depends on its load, and the output resistance on the source impedance. The loading factors in these cases must employ the true amplifier impedances including these bilateral effects. For example, taking the unilateral current amplifier of Figure 3, the corresponding bilateral two-port network is shown in Figure 4 based upon [[Two-port network#Hybrid parameters (h-parameters)| h-parameters]].<ref name=H_port/> Carrying out the analysis for this circuit, the current gain with feedback ''A<sub>fb</sub>'' is found to be


where ''&omega;<sub>C</sub>'' is called the ''corner frequency''. An interesting point is that this frequency becomes infinite (no roll-off) if the Thévenin resistance ''R<sub>Th</sub> = 0''. That is why the parasitic resistance ''r<sub>X</sub>'' in the base lead of the [[hybrid-pi model]] for the bipolar transistor can be influential in determining the amplifier roll-off when these transistors are driven with a very low resistance Thévenin voltage source.
::<math> A_{fb} = \frac {i_L}{i_S} = \frac {A_{loaded}} {1+ {\beta}(R_L/R_S) A_{loaded}} \ . </math>


It is also important to note that the Miller capacitance is not the only source of amplifier frequency dependence. It is important to include as well the capacitances contributed by the output stage, and in [[negative feedback amplifier|feedback amplifiers]] it is this frequency dependence that controls the stability of the amplifier. This frequency dependence can be affected by the dependent current source that the Miller theorem introduces in the output stage.
That is, the ideal current gain ''A<sub>i</sub>'' is reduced not only by the loading factors, but due to the bilateral nature of the two-port by an additional factor<ref>Often called the ''improvement factor'' or the ''desensitivity factor''.</ref> ( 1 + β (R<sub>L</sub> / R<sub>S</sub> ) A<sub>loaded</sub> ), which is typical of [[negative feedback amplifier]] circuits. The factor β (R<sub>L</sub> / R<sub>S</sub> ) is the current feedback provided by the voltage feedback source of voltage gain β V/V. For instance, for an ideal current source with ''R<sub>S</sub>'' = ∞ Ω, the voltage feedback has no influence, and for ''R<sub>L</sub>'' = 0 Ω, there is zero load voltage, again disabling the feedback.
 
The Miller effect is not always a nuisance: it may be exploited to synthesize larger capacitors from smaller ones. One such example is in the stabilization of feedback amplifiers, where the required capacitance may be too large to practically include in the circuit. This may be particularly important in the design of [[integrated circuit]], where capacitors can consume significant area, increasing costs.
 
===Miller approximation===
This example assumes ''A'' is frequency independent, but more generally ''A'' is frequency dependent. Because the Miller capacitance depnds upon ''A'', frequency dependence of ''A'' makes the Miller capacitance frequency dependent, so it is not possible to interpret ''C<sub>M</sub>'' as an everyday capacitance independent of frequency. However, in many cases, frequency dependence of ''A'' arises only at frequencies higher than the corner frequency caused by the Miller effect, so for frequencies up to the Miller-effect roll-off of the gain does not occur, and ''A'' is approximated adequately by its low-frequency value. This approximation, the determination of ''C<sub>M</sub>'' using ''A'' evaluated at low frequencies, is the so-called '''Miller approximation'''.<ref name=Spencer/> So long as the Miller approximation is accurate, ''C<sub>M</sub>'' is frequency independent, and its interpretation as a capacitance is secure.
 
===Mitigation===
The Miller effect may be undesired in many cases, and approaches may be sought to lower its impact. Several such techniques are used in the design of amplifiers.
It is important to notice that the frequency limitation due to ''C''<sub>M</sub> is greatly reduced for low impedance drivers, that is, ''C''<sub>M</sub> ''R<sub>Th</sub>//R<sub>11</sub>'' is small if ''R''<sub>Th</sub> is small. Consequently, one way to minimize the Miller effect upon bandwidth is to use a low-impedance driver, for example, by interposing a [[voltage follower]] stage between the driver and the amplifier This stage acts as an impedance transformer, reducing the apparent driver impedance seen by the amplifier, reducing the Thévenin resistance of the driver.
 
A current buffer stage may be added in front of the load to lower the gain ''A'' across the coupling impedance ''Z<sub>&mu;</sub>'', though not necessarily the overall gain. For example, a [[common base amplifier]] may be used as a current buffer at the output of a [[common emitter amplifier]], forming a [[cascode amplifier]]. Inasmuch as the Miller effect is directly a result of this gain, its reduction will decrease the Miller effect and increase the amplifier bandwidth.


==References and notes==
==References and notes==
{{reflist|refs=
{{reflist|refs=
<ref name=Miller>
{{cite journal |author=John M. Miller |title=Dependence of the input impedance of a three-electrode vacuum tube upon the load in the plate circuit |journal=Scientific Papers of the Bureau of Standards |volume=15 |issue= 351 |pages=pp. 367-385 |year=1920 |url=http://books.google.com/books?id=7u8SAAAAYAAJ&pg=PA367&lpg=PA367}}
</ref>
<ref name=Spencer>
{{cite book
|author=R.R. Spencer and M.S. Ghausi
|title=Introduction to electronic circuit design.
|year= 2003
|page=533
|publisher=Prentice Hall/Pearson Education, Inc.
|location=Upper Saddle River NJ
|isbn=0-201-36183-3
|url=http://worldcat.org/isbn/0-201-36183-3}}
</ref>
<ref name = PoleSplitting>
Ordinarily these effects show up only at frequencies much higher than the [[roll-off]] due to the Miller capacitance, so the analysis presented here is adequate to determine the useful frequency range of an amplifier dominated by the Miller effect. See article on [[pole splitting]].</ref>


<ref name=H_port>>The [[Two-port network#Hybrid parameters (h-parameters)|h-parameter two port]] is the only two-port among the four standard choices that has a current-controlled current source on the output side.</ref>


}}
}}

Latest revision as of 03:07, 22 November 2023


The account of this former contributor was not re-activated after the server upgrade of March 2022.


Figure 1: Schematic of an electrical circuit illustrating current division. Notation RT. refers to the total resistance of the circuit to the right of resistor RX.

In electronics, a current divider is a simple linear circuit that produces an output current (IX) that is a fraction of its input current (IT). The splitting of current between the branches of the divider is called current division. The currents in the various branches of such a circuit divide in such a way as to minimize the total energy expended.

The formula describing a current divider is similar in form to that for the voltage divider. However, the ratio describing current division places the impedance of the unconsidered branches in the numerator, unlike voltage division where the considered impedance is in the numerator. To be specific, if two or more impedances are in parallel, the current that enters the combination will be split between them in inverse proportion to their impedances (according to Ohm's law). It also follows that if the impedances have the same value the current is split equally.

Resistive divider

A general formula for the current IX in a resistor RX that is in parallel with a combination of other resistors of total resistance RT is (see Figure 1):

where IT is the total current entering the combined network of RX in parallel with RT. Notice that when RT is composed of a parallel combination of resistors, say R1, R2, ... etc., then the reciprocal of each resistor must be added to find the total resistance RT:

General case

Although the resistive divider is most common, the current divider may be made of frequency dependent impedances. In the general case the current IX is given by:

Using Admittance

Instead of using impedances, the current divider rule can be applied just like the voltage divider rule if admittance (the inverse of impedance) is used.

Take care to note that YTotal is a straightforward addition, not the sum of the inverses inverted (as you would do for a standard parallel resistive network). For Figure 1, the current IX would be

Example: RC combination

Figure 2: A low pass RC current divider

Figure 2 shows a simple current divider made up of a capacitor and a resistor. Using the formula above, the current in the resistor is given by:

where ZC = 1/(jωC) is the impedance of the capacitor.

The product τ = CR is known as the time constant of the circuit, and the frequency for which ωCR = 1 is called the corner frequency of the circuit. Because the capacitor has zero impedance at high frequencies and infinite impedance at low frequencies, the current in the resistor remains at its DC value IT for frequencies up to the corner frequency, whereupon it drops toward zero for higher frequencies as the capacitor effectively short-circuits the resistor. In other words, the current divider is a low pass filter for current in the resistor.

Loading effect

Figure 3: A current amplifier (gray box) driven by a Norton source (iS, RS) and with a resistor load RL. Current divider in blue box at input (RS,Rin) reduces the current gain, as does the current divider in green box at the output (Rout,RL)

The gain of an amplifier generally depends on its source and load terminations. Current amplifiers and transconductance amplifiers are characterized by a short-circuit output condition, and current amplifiers and transresistance amplifiers are characterized using ideal infinite impedance current sources. When an amplifier is terminated by a finite, non-zero termination, and/or driven by a non-ideal source, the effective gain is reduced due to the loading effect at the output and/or the input, which can be understood in terms of current division.

Figure 3 shows a current amplifier example. The amplifier (gray box) has input resistance Rin and output resistance Rout and an ideal current gain Ai. With an ideal current driver (infinite Norton resistance) all the source current iS becomes input current to the amplifier. However, for a Norton driver a current divider is formed at the input that reduces the input current to

which clearly is less than iS. Likewise, for a short circuit at the output, the amplifier delivers an output current io = Ai ii to the short-circuit. However, when the load is a non-zero resistor RL, the current delivered to the load is reduced by current division to the value:

Combining these results, the ideal current gain Ai realized with an ideal driver and a short-circuit load is reduced to the loaded gain Aloaded:

The resistor ratios in the above expression are called the loading factors. For more discussion of loading in other amplifier types, see loading effect.

Unilateral versus bilateral amplifiers

Figure 4: Current amplifier as a bilateral two-port network; feedback through dependent voltage source of gain β V/V

Figure 3 and the associated discussion refers to a unilateral amplifier. In a more general case where the amplifier is represented by a two port, the input resistance of the amplifier depends on its load, and the output resistance on the source impedance. The loading factors in these cases must employ the true amplifier impedances including these bilateral effects. For example, taking the unilateral current amplifier of Figure 3, the corresponding bilateral two-port network is shown in Figure 4 based upon h-parameters.[1] Carrying out the analysis for this circuit, the current gain with feedback Afb is found to be

That is, the ideal current gain Ai is reduced not only by the loading factors, but due to the bilateral nature of the two-port by an additional factor[2] ( 1 + β (RL / RS ) Aloaded ), which is typical of negative feedback amplifier circuits. The factor β (RL / RS ) is the current feedback provided by the voltage feedback source of voltage gain β V/V. For instance, for an ideal current source with RS = ∞ Ω, the voltage feedback has no influence, and for RL = 0 Ω, there is zero load voltage, again disabling the feedback.

References and notes

  1. ↑ >The h-parameter two port is the only two-port among the four standard choices that has a current-controlled current source on the output side.
  2. ↑ Often called the improvement factor or the desensitivity factor.
Retrieved from "https://citizendium.org/wiki/index.php?title=User:John_R._Brews/WP_Import&oldid=907138"