Cassini ovals: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | |||
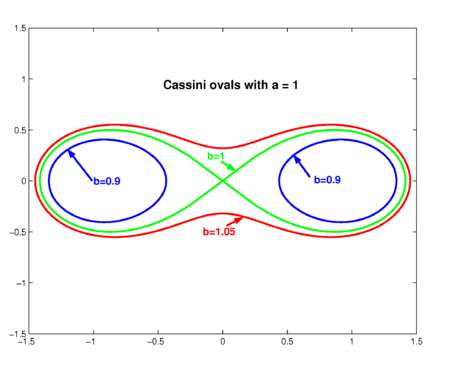
{{Image|Ovals.png|right|450px|Three Cassini ovals. The oval with ''b''<nowiki>=</nowiki>1 is a Bernoulli [[lemniscate]].}} | {{Image|Ovals.png|right|450px|Three Cassini ovals. The oval with ''b''<nowiki>=</nowiki>1 is a Bernoulli [[lemniscate]].}} | ||
A '''Cassini oval''' is a locus of points determined by two fixed points F<sub>1</sub> and F<sub>2</sub> (the "foci") at a distance 2''a'' apart (in the figure the foci are on the ''x''-axis at F<sub>1,2</sub> = ±1). If the distance of a certain point in the plane to F<sub>1</sub> is ''r''<sub>1</sub> and the distance of the same point to F<sub>2</sub> is ''r''<sub>2</sub> then the locus is defined by the product of distances ''r''<sub>1</sub>×''r''<sub>2</sub> being constant and equal to ''b''<sup>2</sup>. | A '''Cassini oval''' is a locus of points determined by two fixed points F<sub>1</sub> and F<sub>2</sub> (the "foci") at a distance 2''a'' apart (in the figure the foci are on the ''x''-axis at F<sub>1,2</sub> = ±1). If the distance of a certain point in the plane to F<sub>1</sub> is ''r''<sub>1</sub> and the distance of the same point to F<sub>2</sub> is ''r''<sub>2</sub> then the locus is defined by the product of distances ''r''<sub>1</sub>×''r''<sub>2</sub> being constant and equal to ''b''<sup>2</sup>. | ||
| Line 4: | Line 5: | ||
The shape of the curves depends on the ratio ''b'' ''':''' ''a''. If ''b'' > ''a'', the curve is a single loop (red curve in the figure)—a dog bone. The case ''a'' = ''b'' produces a [[lemniscate]] of Bernoulli (green curve). The case ''b'' < ''a'' gives two disconnected ovals (eggs). | The shape of the curves depends on the ratio ''b'' ''':''' ''a''. If ''b'' > ''a'', the curve is a single loop (red curve in the figure)—a dog bone. The case ''a'' = ''b'' produces a [[lemniscate]] of Bernoulli (green curve). The case ''b'' < ''a'' gives two disconnected ovals (eggs). | ||
The Cassini ovals are a family of quartic curves, also called Cassini ellipses. They were introduced by Jean-Dominique Cassini (1625–1712), a French-Italian astronomer, who studied them as a possible alternative for the [[Kepler]] elliptic planetary orbits. They did not appear in print until Cassini's son Jacques (1677-1756) published the ''Eléments d'Astronomie'' in | The Cassini ovals are a family of quartic curves, also called Cassini ellipses. They were introduced by Jean-Dominique Cassini (1625–1712), a French-Italian astronomer, who studied them as a possible alternative for the [[Kepler]] elliptic planetary orbits.<ref>J. Sivardiere, ''Kepler ellipse or Cassini oval?'', European Journal of Physics, vol. '''15''', pp. 62-64 (1994)</ref> | ||
They did not appear in print until Cassini's son Jacques (1677-1756) published the ''Eléments d'Astronomie'' in 1740. | |||
==Equations== | ==Equations== | ||
| Line 21: | Line 23: | ||
were made. | were made. | ||
The equation may be cast in a slightly different form | The equation may be cast in a slightly different form, the ''Cartesian equation of the Cassini oval'', | ||
:<math> | :<math> | ||
(x^2+y^2+1)^2 - 4x^2 | (x^2+y^2+1)^2 - 4x^2 - b^4 = 0.\; | ||
</math> | </math> | ||
Substitution of | Substitution of | ||
| Line 37: | Line 39: | ||
r^4 -2r^2\cos2\theta +1 - b^4 =0. \, | r^4 -2r^2\cos2\theta +1 - b^4 =0. \, | ||
</math> | </math> | ||
===Plotting=== | |||
A few words about plotting the Cassini ovals may be useful. | |||
The polar equation is a quadratic equation in ''r''<sup>2</sup>. It has real roots if the [[discriminant]] ''D'' is positive or zero, | |||
:<math> | :<math> | ||
D \equiv 4\cos^2 2\theta - 4+4b^4 \ge 0 \Longrightarrow b^4 \ge 1-\cos^2 2\theta. | D \equiv 4\cos^2 2\theta - 4+4b^4 \ge 0 \Longrightarrow b^4 \ge 1-\cos^2 2\theta. | ||
</math> | </math> | ||
Because 0 ≤ cos<sup>2</sup> 2θ ≤ 1, this condition is satisfied for all θ if ''b'' ≥ 1 (= ''a''). Hence in the case of the lemniscate (''b'' = 1) and the dog bone (''b'' > 1) the quantity ''r''<sup>2</sup> may be solved from the polar equation. Since ''r''<sup>2</sup> must be positive, one of the two roots (the one with −''D'') can be discarded. | Because 0 ≤ cos<sup>2</sup> 2θ ≤ 1, this condition is satisfied for all θ if ''b'' ≥ 1 (= ''a''). Hence in the case of the lemniscate (''b'' = 1) and the dog bone (''b'' > 1) the quantity ''r''<sup>2</sup> may be solved from the polar equation. Since ''r''<sup>2</sup> must be positive, one of the two roots (the one with −''D'') can be discarded. Now ''r'' > 0 follows by taking a square root and the Cassini ovals for ''b'' ≥ ''a'' (=1) can be drawn as polar plots, as is shown in the figure. | ||
The case ''b'' < 1 requires a different approach. If one looks at the figure (at the "eggs") one sees that there is range of ''x''-values on the positive axis and a mirror range on the negative ''x''-axis where the function is defined. The boundary points ''x''<sub>0</sub> of the ranges are given by ''y'' = 0 (where the ovals cross the ''x''-axis). Introducing ''y'' = 0 into the Cartesian form one derives easily (and remember ''b''<sup>2</sup> < 1) | |||
:<math> | |||
x^2_0 = 1 \plusmn b^2 \Longrightarrow -\sqrt{1+b^2} \le x \le -\sqrt{1-b^2}\quad\hbox{and}\quad \sqrt{1-b^2} \le x \le \sqrt{1+b^2}. | |||
</math> | |||
If one restricts ''x'' to these two intervals, a positive and negative ''y''-value can be solved for given ''x'' from the Cartesian equation. In this way one obtains ''y'' as function of ''x'' and a graph may be plotted. | |||
==Reference== | |||
<references /> | |||
Latest revision as of 07:48, 29 December 2009
A Cassini oval is a locus of points determined by two fixed points F1 and F2 (the "foci") at a distance 2a apart (in the figure the foci are on the x-axis at F1,2 = ±1). If the distance of a certain point in the plane to F1 is r1 and the distance of the same point to F2 is r2 then the locus is defined by the product of distances r1×r2 being constant and equal to b2.
The shape of the curves depends on the ratio b : a. If b > a, the curve is a single loop (red curve in the figure)—a dog bone. The case a = b produces a lemniscate of Bernoulli (green curve). The case b < a gives two disconnected ovals (eggs).
The Cassini ovals are a family of quartic curves, also called Cassini ellipses. They were introduced by Jean-Dominique Cassini (1625–1712), a French-Italian astronomer, who studied them as a possible alternative for the Kepler elliptic planetary orbits.[1] They did not appear in print until Cassini's son Jacques (1677-1756) published the Eléments d'Astronomie in 1740.
Equations
If one takes the foci on the x-axis at ±a, the family of loci is given by
Without loss of generality one may take a as a new unit of distance (rescaling). Then the equation may be written as
where both sides of the equation were divided by a4 and the substitutions
were made.
The equation may be cast in a slightly different form, the Cartesian equation of the Cassini oval,
Substitution of
gives the form
Whence the polar equation of the Cassini oval is,
Plotting
A few words about plotting the Cassini ovals may be useful.
The polar equation is a quadratic equation in r2. It has real roots if the discriminant D is positive or zero,
Because 0 ≤ cos2 2θ ≤ 1, this condition is satisfied for all θ if b ≥ 1 (= a). Hence in the case of the lemniscate (b = 1) and the dog bone (b > 1) the quantity r2 may be solved from the polar equation. Since r2 must be positive, one of the two roots (the one with −D) can be discarded. Now r > 0 follows by taking a square root and the Cassini ovals for b ≥ a (=1) can be drawn as polar plots, as is shown in the figure.
The case b < 1 requires a different approach. If one looks at the figure (at the "eggs") one sees that there is range of x-values on the positive axis and a mirror range on the negative x-axis where the function is defined. The boundary points x0 of the ranges are given by y = 0 (where the ovals cross the x-axis). Introducing y = 0 into the Cartesian form one derives easily (and remember b2 < 1)
If one restricts x to these two intervals, a positive and negative y-value can be solved for given x from the Cartesian equation. In this way one obtains y as function of x and a graph may be plotted.
Reference
- ↑ J. Sivardiere, Kepler ellipse or Cassini oval?, European Journal of Physics, vol. 15, pp. 62-64 (1994)
![{\displaystyle \left[(x-a)^{2}+y^{2}\right]\left[(x+a)^{2}+y^{2}\right]=b^{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9e6eb1a983a1b579fd0a7303c38114483cd3ea)
![{\displaystyle \left[(x-1)^{2}+y^{2}\right]^{2}\left[(x+1)^{2}+y^{2}\right]^{2}=b^{4},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8174e16d5b0d5be99a533074176a2fb0971f76e3)






