Surface-based morphometry: Difference between revisions
imported>Daniel Mietchen (image legend) |
mNo edit summary |
||
| (14 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
In [[neuroimaging]], '''surface-based morphometry''' (often abbreviated SBM) is a group of [[brain morphometric]] techniques used to [[surface reconstruction|construct]] and analyze surfaces that represent structural boundaries | In [[neuroimaging]], '''surface-based morphometry''' (often abbreviated SBM) is a group of [[brain morphometric]] techniques used to [[surface reconstruction|construct]] and analyze [[cortical surface|surfaces]] that represent structural boundaries within the [[brain]]. As such, it differs from [[voxel-based morphometry|voxel-]] and [[deformation-based morphometry|deformation-based]] morphometric approaches, which ultimately analyze image properties at the level of [[voxel]]s. | ||
{{Image|SBM image processing steps.png|left|650px|The major steps involved in surface-based morphometry of the brain: [[Neuroimaging|Image acquisition]], [[surface reconstruction]], [[surface inflation]] and [[surface mapping]]. The transition from A to B requires a set of [[preprocessing (neuroimaging)|preprocessing]] steps whose major elements are shared with [[voxel-based morphometry|voxel-]] and [[deformation-based morphometry]]: [[image registration]], [[intensity normalization]], [[brain extraction]] and [[brain segmentation]].}} | {{Image|SBM image processing steps.png|left|650px|The major steps involved in surface-based morphometry of the brain: [[Neuroimaging|Image acquisition]], [[surface reconstruction]], [[surface inflation]] (green representing [[gyral]] regions, red [[sulcal]] ones) and [[surface mapping]]. The transition from A to B requires a set of [[preprocessing (neuroimaging)|preprocessing]] steps whose major elements are shared with [[voxel-based morphometry|voxel-]] and [[deformation-based morphometry|deformation-based]] [[brain morphometry|morphometry]]: [[image registration]], [[intensity normalization]], [[smoothing]], [[Skull stripping|brain extraction]] and [[brain segmentation]].}} | ||
These boundaries are defined by or on the basis of a [[brain segmentation]], and the surface is generated by a [[meshing]] algorithm (e.g. [[marching cubes]]) that codifies relationships between [[voxels]] on the boundary into relationships between [[polygon]]al or [[polyhedral]] surface elements. | These boundaries — e.g. that between the [[grey matter]] of the [[cerebral cortex]] and the underlying [[white matter]], often referred to as the [[white matter surface]] — are defined by or on the basis of a [[brain segmentation]], and the corresponding surface is generated by a [[meshing]] algorithm (e.g. [[marching cubes]]) that codifies relationships between [[voxels]] on the boundary into relationships between [[polygon]]al or [[polyhedral]] surface elements. | ||
This does not require [[image registration|registering]] the individual brain images to a template brain, though comparisons across brains demand a reference surface that belongs to the same [[topological genus]] (i.e. 0) and is normalized in size. The brains are thus mapped to a [[unit sphere]] on which their original properties can be compared with each other, and results are | This does not require [[image registration|registering]] the individual brain images to a template brain, though comparisons across brains demand a reference surface that belongs to the same [[topological genus]] (i.e. 0) and is normalized in size. The brains are thus [[brain mapping|mapped]] to a [[unit sphere]] on which their original properties can be compared with each other, and results are mapped back to a reference cortical surface. | ||
The surfaces most appropriate for cortical analyses are the boundaries between white and grey matter or between grey matter and [[cerebrospinal fluid]] (the latter surface is also often referred to as pial surface, since the [[pia mater]] is not commonly [[brain segmentation|segmented]] into a class of its own) but various representations of the so-called central surface (roughly corresponding to the anatomical lamina IV) are also in use. For some [[subcortical]] structures (e.g. the [[hippocampus]] or [[basal ganglia]]), appropriate surfaces can be defined in a similar way, while lateral delineation of the | The surfaces most appropriate for cortical analyses are the boundaries between white and grey matter or between grey matter and [[cerebrospinal fluid]] (the latter surface is also often referred to as pial surface, since the [[pia mater]] is not commonly [[brain segmentation|segmented]] into a class of its own) but various representations of the so-called central surface (roughly corresponding to the anatomical lamina IV) are also in use. For some [[subcortical]] structures (e.g. the [[hippocampus]] or [[basal ganglia]]), appropriate surfaces can be defined in a similar way, while lateral delineation of the corpus callosum, for instance, is difficult. | ||
Statistical analyses in surface-based morphometry are based on properties of the individual mesh elements and aggregations thereof. | Statistical analyses in surface-based morphometry are based on properties of the individual mesh elements and aggregations thereof. | ||
These latter ones include, foremostly, | These latter ones include, foremostly, | ||
some measure of the distance between different surfaces | some measure of the distance between different surfaces — typically the [[cortical thickness]] — or [[sulcal depth]] | ||
but also | but also | ||
some local or global measures of [[cortical surface area|area]], [[curvature (mathematics)|curvature]] (e.g. [[gyrification]]) or overall shape (e.g. via [[spherical wavelets]], [[spherical harmonics]] or [[Laplace-Beltrami spectra]]). | some local or global measures of [[cortical surface area|area]], [[curvature (mathematics)|curvature]] (e.g. [[gyrification]]) or overall shape (e.g. via [[spherical wavelets]], [[spherical harmonics]] or [[Laplace-Beltrami spectra]]). | ||
[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 16:00, 23 October 2024
In neuroimaging, surface-based morphometry (often abbreviated SBM) is a group of brain morphometric techniques used to construct and analyze surfaces that represent structural boundaries within the brain. As such, it differs from voxel- and deformation-based morphometric approaches, which ultimately analyze image properties at the level of voxels.
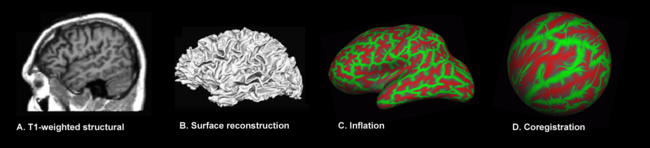
The major steps involved in surface-based morphometry of the brain: Image acquisition, surface reconstruction, surface inflation (green representing gyral regions, red sulcal ones) and surface mapping. The transition from A to B requires a set of preprocessing steps whose major elements are shared with voxel- and deformation-based morphometry: image registration, intensity normalization, smoothing, brain extraction and brain segmentation.
These boundaries — e.g. that between the grey matter of the cerebral cortex and the underlying white matter, often referred to as the white matter surface — are defined by or on the basis of a brain segmentation, and the corresponding surface is generated by a meshing algorithm (e.g. marching cubes) that codifies relationships between voxels on the boundary into relationships between polygonal or polyhedral surface elements.
This does not require registering the individual brain images to a template brain, though comparisons across brains demand a reference surface that belongs to the same topological genus (i.e. 0) and is normalized in size. The brains are thus mapped to a unit sphere on which their original properties can be compared with each other, and results are mapped back to a reference cortical surface.
The surfaces most appropriate for cortical analyses are the boundaries between white and grey matter or between grey matter and cerebrospinal fluid (the latter surface is also often referred to as pial surface, since the pia mater is not commonly segmented into a class of its own) but various representations of the so-called central surface (roughly corresponding to the anatomical lamina IV) are also in use. For some subcortical structures (e.g. the hippocampus or basal ganglia), appropriate surfaces can be defined in a similar way, while lateral delineation of the corpus callosum, for instance, is difficult.
Statistical analyses in surface-based morphometry are based on properties of the individual mesh elements and aggregations thereof. These latter ones include, foremostly, some measure of the distance between different surfaces — typically the cortical thickness — or sulcal depth but also some local or global measures of area, curvature (e.g. gyrification) or overall shape (e.g. via spherical wavelets, spherical harmonics or Laplace-Beltrami spectra).