Fixed point: Difference between revisions
imported>Dmitrii Kouznetsov |
mNo edit summary |
||
| (38 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{Subpages}} | ||
A '''fixed point''' is a point in the domain of a [[function (mathematics)|function]] that is mapped to itself. Thus, a fixed point of a function ''f'' is a point ''x'' such that <math>f(x) = x</math>. | |||
==Examples== | |||
: | The squaring function is the function that maps each number to its [[square (arithmetics)|square]], so a fixed point of the squaring function is a number that equals its square. There are two such numbers: 0 and 1. | ||
= | In similar way, 0 is fixed point of [[sine]] function, because <math>\sin(0)=0</math>. | ||
The function ''f'' can also be a [[linear operator]]. In this case, the fixed point is an [[eigenvector]] with [[eigenvalue]] equal to unity. For instance, the [[exponential function]] is a fixed point of the [[differential operator]] because the derivative of e<sup>''x''</sup> is again e<sup>''x''</sup>. Similarly, the [[Gaussian exponential]] exp(−''x''<sup>2</sup>/2) is a fixed point of the [[Fourier transform]] operator <math>\mathcal{F}</math> defined by | |||
:<math> \mathcal{F}[f](p) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(x) \exp(-{\rm i}px) \, {\rm d}x. </math> <ref>The expression <math>\mathcal{F}[f](p)</math> on the left-hand side means the value at ''p'' of the Fourier transform <math>\mathcal{F}[f]</math>; the Fourier transform is the result of applying the operator <math>\mathcal{F}</math> to the function ''f''.</ref> | |||
[[ | |||
because | |||
< | |||
is fixed point of the [[Fourier | |||
: | |||
<ref | |||
<math>F | |||
</ref> | |||
==Fixed points of [[exponential]] and fixed points of [[logarithm]]== | ==Fixed points of [[exponential]] and fixed points of [[logarithm]]== | ||
| Line 41: | Line 20: | ||
in the complex <math>z</math>-plane | in the complex <math>z</math>-plane | ||
]]<!-- | ]]<!-- | ||
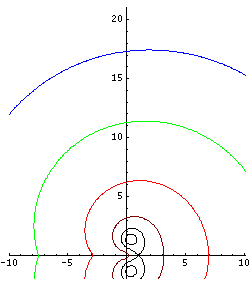
[[Image:FixedPointsExpe00.jpg|300px|right|thumb|Graphical search for fixed points of [[exponential]]. Function | [[Image:FixedPointsExpe00.jpg|300px|right|thumb|Graphical search for fixed points of [[exponential]]. Function <math>f=|z-\exp(z)|</math> is shown with levels | ||
<math>f=0.5</math>, | |||
<math>f=1</math>, | |||
<math>f=2</math>, | |||
<math>f=4</math>, | |||
<math>f=8</math>, | |||
<math>f=16</math> | |||
in the complex | in the complex <math>z</math>-plane | ||
]]!--> | ]]!--> | ||
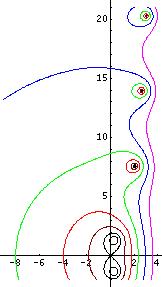
[[Image:FixedPointsExpe00.jpg|300px|right|thumb|Fig.2. The same as FIg.1 for function <math>f=|z-\exp(z)|</math> | [[Image:FixedPointsExpe00.jpg|300px|right|thumb|Fig.2. The same as FIg.1 for function <math>f=|z-\exp(z)|</math> | ||
| Line 54: | Line 33: | ||
Fixed points can be searched graphically. Fig.1 shows the graphical search of fixed points of [[logarithm]], | Fixed points can be searched graphically. Fig.1 shows the graphical search of fixed points of [[logarithm]], | ||
i.e., | i.e., solutions of the equation | ||
:(10) <math> L=\ln(L) </math> | :(10) <math> L=\ln(L) </math> | ||
There are no real solutions | There are no real solutions for this equation, but there are two complex-conjugated solutions | ||
<math>L_{\rm e}</math> and <math>L_{\rm e}^*</math>. However, the value of <math>L_{\rm e}</math> cannot be estimated well from the figure (1), but the | <math>L_{\rm e}</math> and <math>L_{\rm e}^*</math>. However, the value of <math>L_{\rm e}</math> cannot be estimated well from the figure (1), but the straightforward iteration allows the precise estimate. Few hundreds of iterations are sufficient to get error of order of last significant figure in the | ||
approximation | approximation | ||
:(11) <math>L_{\rm e} \approx 0.318131505204764135312654+1.33723570143068940890116 \!~\rm i</math> | :(11) <math>L_{\rm e} \approx 0.318131505204764135312654+1.33723570143068940890116 \!~\rm i</math> | ||
===Fixed points of exp are not the same as those of ln=== | ===Fixed points of exp are not the same as those of ln=== | ||
Fixed points of logarithm should not be | Fixed points of logarithm should not be confused with fixed points of exponential, shown in FIgure 2. | ||
These fixed points are solutions of equations | |||
:(12) <math>L=\exp(L)</math> | :(12) <math>L=\exp(L)</math> | ||
They can be expressed also as solution of equation | They can be expressed also as solution of equation | ||
| Line 70: | Line 49: | ||
2.062277729598284 + 7.5886311784725127 \!~\rm i | 2.062277729598284 + 7.5886311784725127 \!~\rm i | ||
</math> | </math> | ||
is fixed point of the exponential, but is not | is fixed point of the exponential, but is not fixed point of natural logarithm. | ||
In the case of exponential and natural logarithm, all fixed points are complex. | In the case of exponential and natural logarithm, all fixed points are complex. | ||
| Line 78: | Line 57: | ||
2 and 4 are their fixed points. | 2 and 4 are their fixed points. | ||
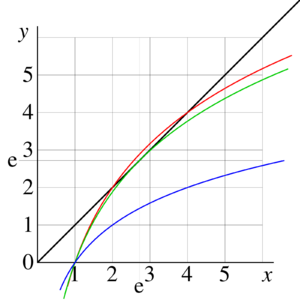
{{Image|ExampleEquationLog01.png|right|300px|FIg.3. Example of graphic solution of equation | |||
<math>x=\log_b(x)</math> for | <math>x=\log_b(x)</math> for | ||
<math>b=\sqrt{2}</math> (two real solutions, <math>x=2</math> and <math>x=4</math>), | <math>b=\sqrt{2}</math> (two real solutions, <math>x=2</math> and <math>x=4</math>), | ||
<math>b=\exp(1/\rm e)</math> (one real solution <math>x=\rm e</math>) | <math>b=\exp(1/\rm e)</math> (one real solution <math>x=\rm e</math>) | ||
<math>b=2</math> (no real solutions). | <math>b=2</math> (no real solutions).}} | ||
Finding of real fixed points is presented graphically in Figure 3. The black curve represents the identical function <math>f=f(x)=x</math> in the left hand side of equation | Finding of real fixed points is presented graphically in Figure 3. The black curve represents the identical function <math>f=f(x)=x</math> in the left hand side of equation | ||
:(14) <math> z=\log_b(z)</math> | :(14) <math> z=\log_b(z)</math> | ||
the colored curves represent the function in the right hand side for | the colored curves represent the function in the right hand side for | ||
<math>b=\sqrt{2}</math> | <math>b=\sqrt{2}</math>, | ||
<math>b=\exp(1/\rm e</math> | <math>b=\exp(1/\rm e)</math>, and | ||
<math>b=2</math>. In the last case, there are no real solutions, but the complex fixed points are complex numbers <math>L_2</math> and <math>L_2^*</math>. Within few hundred iterations of equation (14), they can be | <math>b=2</math>. In the last case, there are no real solutions, but the complex fixed points are complex numbers <math>L_2</math> and <math>L_2^*</math>. Within few hundred iterations of equation (14), they can be approximated with many decimal digits; | ||
:(15)<math> L_2 \approx 0.824678546142074222314065+1.56743212384964786105857 \!~\rm i | :(15)<math> L_2 \approx 0.824678546142074222314065+1.56743212384964786105857 \!~\rm i | ||
</math>. | </math>. | ||
Such evaluation can be | Such evaluation can be performed [[in real time]] with any high level [[algorithmic language]] – Maple, Mathematica, that allow to specify number of correct decimal digits desirable in the result. | ||
The mathematical proof of existence of the fixed points of the exponential can be found in the old paper by [[Helmuth Kneser]] | |||
<ref name="knes50"> {{cite journal | |||
| author=Helmuth Kneser | |||
| title= Reelle analytische Lösungen der Gleichung <math> \varphi \big( \varphi(x)\big) = {\rm e}^x</math> und verwandter Funktionalgleichungen | |||
| journal=Journal für die reine und angewandte Mathematik | |||
| volume=187 | |||
| pages=8-67 | |||
}}</ref>. Recently, [[Henryk Trappmann]] had generalized this proof for the exponentiation of arbitrary real base, but his theorem is not yet uploaded. | |||
===Tetration=== | ===Tetration=== | ||
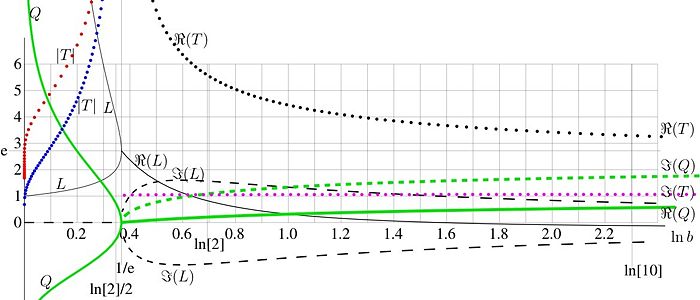
{{Image|TetrationAsymptoticParameters01.jpg|left|700px|FIg.4. parameters of asymptotic of tetration versus logarithm of the base}} | |||
The fixed points of logarithm determine the asymptotic properties of analytic extension of [[tetration]] <math>F_b</math>. In some range of the | The fixed points of logarithm determine the asymptotic properties of analytic extension of [[tetration]] <math>F_b</math>. In some range of the | ||
complex <math>x</math>-plane, the tetration can be approximated with asymptotic | complex <math>x</math>-plane, the tetration can be approximated with asymptotic | ||
| Line 99: | Line 88: | ||
(32) <math> F(z)=L+\varepsilon(z) + o \big(\varepsilon(z)^{2}\big) </math> | (32) <math> F(z)=L+\varepsilon(z) + o \big(\varepsilon(z)^{2}\big) </math> | ||
where | where | ||
(33) <math> \varepsilon(z)=\exp(Qz+r) </math> | (33) <math> \varepsilon(z)=\exp(Qz+r) </math> | ||
<math>Q</math> and <math>r</math> are fixed complex numbers, dependent on <math>b</math>. | <math>Q</math> and <math>r</math> are fixed complex numbers, dependent on <math>b</math>. | ||
Possible values of fixed points <math>L</math> are shown with thin black curves versus logarithm on base <math>b</math>. | Possible values of fixed points <math>L</math> are shown with thin black curves versus logarithm on base <math>b</math>. | ||
At <math>\ln(b)>1/\rm e</math>, the fixed points are complex; the real part is shown with solid curve, the imaginary part is shown with dashed curve. | At <math>\ln(b)>1/\rm e</math>, the fixed points are complex; the real part is shown with solid curve, the imaginary part is shown with dashed curve. | ||
Green curves in | Green curves in Figure 4 represent the parameter <math> Q</math> in (33), again, the dashed curve shows the imaginary part, and | ||
real and imaginary parts of the asymptotic period <math> 2\pi{ \rm i}/Q</math>. See article [[tetration]] for details. | real and imaginary parts of the asymptotic period <math> 2\pi{ \rm i}/Q</math>. See article [[tetration]] for details. | ||
==Expression through the special functions== | |||
In some range of values of <math>b</math>, and in particular, for <math>b>1</math>, the fixed point <math>L</math> of <math>\log_b</math> can be expressed through the [[LambertW]] function, | |||
: <math>L=-\mathrm{LambertW}(-\ln(b))/\ln(b)</math> | |||
Function LamnertW is implemented in many [[programming languages]]. | |||
The special name [[Filog]] is suggested for the function, that expresses one of the fixed point of logarithm through the logarithm of its base | |||
<ref name="filog"> | |||
http://tori.ils.uec.ac.jp/TORI/index.php/Filog <math>~ f=\mathrm{Filog}(z)</math> is solution of the equation <math>\log_b(f)\!=\!f </math> | |||
for base <math>b\!=\!\exp(z)</math> | |||
</ref>: | |||
: <math>L=\mathrm{Filog}(\ln(b))</math> | |||
Another fixed point can be expressed as <math>\mathrm{Filog}(\ln(b)^*)^*</math><br> | |||
Function Filog is simply related with the [[Tania function]]: | |||
: <math>\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1-\mathrm{i}\big)}{-z} </math> | |||
This representation can be used in the whole complex plane; it is more robust than the representation above through the [[LambertW]] function. | |||
==[[Projector(mathematics)|Projector]]s== | ==[[Projector(mathematics)|Projector]]s== | ||
Functor <math>P</math> on the space < | Functor <math>P</math> on the space <math> \Psi</math> is called [[Projector(mathematics)|Projector]], if <math>P^2 \phi=P \phi</math> for all <math>\phi \in \Psi</math>. | ||
Any | Any function <math> f </math> of subset <math>\psi </math> of functions <math>f=P\phi</math> | ||
is fixed point of projector <math>P</math>. | is fixed point of projector <math>P</math>. | ||
In common use are projectors of the 3-dimensional space to 2-dimensional space. Such | In common use are projectors of the 3-dimensional space to 2-dimensional space. Such projectors allow to make flat pictures of 3-dimensional objects. Any point at the plane of image is fixed point of such a projector. | ||
===Common fixed points=== | |||
The same element <math>f</math> may be fixed point of several functors. | |||
Sometimes, such common fixed points can be approximated using iterations. | |||
If there are two projectors <math>P_1</math> and <math>P_2</math>, then | |||
the sequence of elements, approximating the common fixed point of these projectors can be constructed in the following way: | |||
: <math>f_n=P_1\Big(P_2(f_{n-1})\Big) </math> | |||
Such a sequence is used to approximate the [[amplitude-phase behavior]] of [[ultra-short pulses]] in the | |||
[[Frequency Resolved Optical Gating|FROG]] systems <ref name="frog"> | |||
Rick Trebino, Kenneth W. DeLong, David N. Fittinghoff, John N. Sweetser, Marco A. Krumbügel, and Bruce A. Richman. | |||
Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. | |||
Rev. Sci. Instrum. 68, 3277 (1997); DOI:10.1063/1.1148286 | |||
</ref><ref> | |||
Giulio Cerullo and Sandro De Silvestri. | |||
Ultrafast optical parametric amplifiers. | |||
Rev. Sci. Instrum. 74, 1 (2003); DOI:10.1063/1.1523642 | |||
</ref>. | |||
Amplitude and phase in ultra-short pulses can be measured only with another ultra-short pulse; so, some nonlinear interaction is used to recover the temporal behavior of the pulse. The set of equations (usually two) is solved numerically, projecting the probe function to the spaces of solutions of each equation sequentially. | |||
==Notes== | ==Notes== | ||
{{reflist}}[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 06:00, 17 August 2024
A fixed point is a point in the domain of a function that is mapped to itself. Thus, a fixed point of a function f is a point x such that .
Examples
The squaring function is the function that maps each number to its square, so a fixed point of the squaring function is a number that equals its square. There are two such numbers: 0 and 1.
In similar way, 0 is fixed point of sine function, because .
The function f can also be a linear operator. In this case, the fixed point is an eigenvector with eigenvalue equal to unity. For instance, the exponential function is a fixed point of the differential operator because the derivative of ex is again ex. Similarly, the Gaussian exponential exp(−x2/2) is a fixed point of the Fourier transform operator defined by
Fixed points of exponential and fixed points of logarithm
Fixed points can be searched graphically. Fig.1 shows the graphical search of fixed points of logarithm, i.e., solutions of the equation
- (10)
There are no real solutions for this equation, but there are two complex-conjugated solutions and . However, the value of cannot be estimated well from the figure (1), but the straightforward iteration allows the precise estimate. Few hundreds of iterations are sufficient to get error of order of last significant figure in the approximation
- (11)
Fixed points of exp are not the same as those of ln
Fixed points of logarithm should not be confused with fixed points of exponential, shown in FIgure 2. These fixed points are solutions of equations
- (12)
They can be expressed also as solution of equation
- (13) for some integer
For example, at
- (13)
is fixed point of the exponential, but is not fixed point of natural logarithm.
In the case of exponential and natural logarithm, all fixed points are complex. However, the real fixed points exist at . For example, at , number e is fixed point of both, and ; and at , numbers 2 and 4 are their fixed points.
Finding of real fixed points is presented graphically in Figure 3. The black curve represents the identical function in the left hand side of equation
- (14)
the colored curves represent the function in the right hand side for , , and . In the last case, there are no real solutions, but the complex fixed points are complex numbers and . Within few hundred iterations of equation (14), they can be approximated with many decimal digits;
- (15).
Such evaluation can be performed in real time with any high level algorithmic language – Maple, Mathematica, that allow to specify number of correct decimal digits desirable in the result.
The mathematical proof of existence of the fixed points of the exponential can be found in the old paper by Helmuth Kneser [2]. Recently, Henryk Trappmann had generalized this proof for the exponentiation of arbitrary real base, but his theorem is not yet uploaded.
Tetration
The fixed points of logarithm determine the asymptotic properties of analytic extension of tetration . In some range of the complex -plane, the tetration can be approximated with asymptotic
(32)
where
(33)
and are fixed complex numbers, dependent on . Possible values of fixed points are shown with thin black curves versus logarithm on base . At , the fixed points are complex; the real part is shown with solid curve, the imaginary part is shown with dashed curve.
Green curves in Figure 4 represent the parameter in (33), again, the dashed curve shows the imaginary part, and real and imaginary parts of the asymptotic period . See article tetration for details.
Expression through the special functions
In some range of values of , and in particular, for , the fixed point of can be expressed through the LambertW function,
Function LamnertW is implemented in many programming languages.
The special name Filog is suggested for the function, that expresses one of the fixed point of logarithm through the logarithm of its base [3]:
Another fixed point can be expressed as
Function Filog is simply related with the Tania function:
This representation can be used in the whole complex plane; it is more robust than the representation above through the LambertW function.
Projectors
Functor on the space is called Projector, if for all .
Any function of subset of functions is fixed point of projector .
In common use are projectors of the 3-dimensional space to 2-dimensional space. Such projectors allow to make flat pictures of 3-dimensional objects. Any point at the plane of image is fixed point of such a projector.
Common fixed points
The same element may be fixed point of several functors.
Sometimes, such common fixed points can be approximated using iterations. If there are two projectors and , then the sequence of elements, approximating the common fixed point of these projectors can be constructed in the following way:
Such a sequence is used to approximate the amplitude-phase behavior of ultra-short pulses in the FROG systems [4][5]. Amplitude and phase in ultra-short pulses can be measured only with another ultra-short pulse; so, some nonlinear interaction is used to recover the temporal behavior of the pulse. The set of equations (usually two) is solved numerically, projecting the probe function to the spaces of solutions of each equation sequentially.
Notes
- ↑ The expression on the left-hand side means the value at p of the Fourier transform ; the Fourier transform is the result of applying the operator to the function f.
- ↑ Helmuth Kneser. "Reelle analytische Lösungen der Gleichung und verwandter Funktionalgleichungen". Journal für die reine und angewandte Mathematik 187: 8-67.
- ↑ http://tori.ils.uec.ac.jp/TORI/index.php/Filog is solution of the equation for base
- ↑ Rick Trebino, Kenneth W. DeLong, David N. Fittinghoff, John N. Sweetser, Marco A. Krumbügel, and Bruce A. Richman. Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. Rev. Sci. Instrum. 68, 3277 (1997); DOI:10.1063/1.1148286
- ↑ Giulio Cerullo and Sandro De Silvestri. Ultrafast optical parametric amplifiers. Rev. Sci. Instrum. 74, 1 (2003); DOI:10.1063/1.1523642



={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)\exp(-{\rm {i}}px)\,{\rm {d}}x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f7d05dbdca39ffb2bd527e085ca118e225581df)



























































}](https://wikimedia.org/api/rest_v1/media/math/render/svg/017a97e3f0c147c2decb79f1d78e029f91ef95b3)
![{\displaystyle {\mathcal {F}}[f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84a4ecfeb48a40b6273d5b9e11c1bbe685455d8)



