imported>Gordan Feric |
imported>Caesar Schinas |
| (31 intermediate revisions by 6 users not shown) |
| Line 1: |
Line 1: |
| {{TOC-right}}
| | <big>Move into cold storage [http://en.citizendium.org/wiki?title=User_talk:Milton_Beychok&curid=100050940&diff=100443467&oldid=100443454&rcid=602465 due to editors decision].</big> [[User:Chris Day|Chris Day]] 08:04, 2 February 2009 (UTC) |
| This article addresses analysis of energy conversion as it pertains to power cycles (Carnot, Brayton, Otto and Diesel), power cycle components/processes (compression, combustion and expansion) and compressible flow (nozzle, diffuser and thrust) ideal operation, T-s diagrams and performance trends. | | |
| {{editintro}}
| | This article addresses analysis of '''energy conversion''' as it pertains to power cycles (Carnot, Brayton, Otto and Diesel), power cycle components/processes (compression, combustion and expansion) and compressible flow (nozzle, diffuser and thrust) ideal operation, T-s diagrams and performance trends. |
| | |
| ==Power cycle analysis== | | ==Power cycle analysis== |
|
| |
|
| Line 8: |
Line 9: |
| ===Carnot cycle=== | | ===Carnot cycle=== |
|
| |
|
| In the presented Carnot cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT. | | In the presented Carnot cycle analysis, only air is considered as the working fluid and behaving as a perfect gas. Specific heat has a constant value. Ideal gas state equation is valid, that is pv = RT. |
| | |
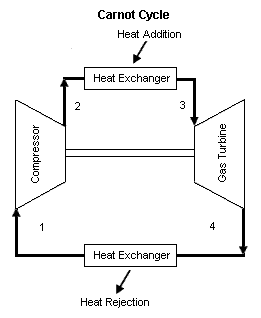
| Figure 1 contains a Carnot cycle schematic layout. Air enters a compressor at point 1, and exits the compressor at point 2. Isentropic compression is considered with no entropy change. Air enters a heat exchanger -- heat addition -- at point 2, and exits the heat exchanger at point 3. At a constant temperature, heat addition takes place. Air enters a turbine at point 3, and exits the turbine at point 4. Isentropic expansion is considered with no entropy change. Air enters a heat exchanger -- heat rejection -- at point 4, and exits the heat exchanger at point 1. At a constant temperature, heat rejection takes place. It should be mentioned that air at point 1 enters the compressor and the cycle is repeated.
| |
| [[Image:ESC31.gif|center]]
| |
| <center>Figure 1 - Carnot Cycle Schematic Layout</center>
| |
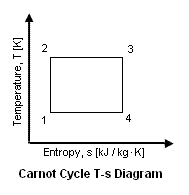
| Figure 2 presents a Carnot Cycle entropy vs temperature diagram.
| |
| [[Image:ESC32.gif|center]]
| |
| <center>Figure 2 - Carnot Cycle Temperature vs Entropy Diagram</center>
| |
| The thermal cycle efficiency can be given as a function of specific external work (specific net power output) and added heat to the working fluid as follows:
| |
| | |
| η = w/q<sub>h</sub> = (w<sub>t</sub> - w<sub>c</sub>)/q<sub>h</sub> = (q<sub>h</sub> - q<sub>l</sub>)/q<sub>h</sub> = 1 - q<sub>l</sub>/q<sub>h</sub> = 1 - T<sub>1</sub>Δs/T<sub>2</sub>Δs = 1 - T<sub>1</sub>/T<sub>2</sub> = 1 - T<sub>R</sub>/T<sub>A</sub>
| |
| | |
| where
| |
| | |
| η - thermal efficiency [/]
| |
| | |
| w - specific external work (specific net power output) [kJ/kg]
| |
| | |
| w<sub>t</sub> - expansion specific power output [kJ/kg]
| |
| | |
| w<sub>c</sub> - compression specific power input [kJ/kg]
| |
| | |
| q<sub>h</sub> - added heat to the working fluid [kJ/kg]
| |
| | |
| q<sub>l</sub> - heat rejected from the working fluid [kJ/kg]
| |
| | |
| Δs - entropy change during heat addition and heat rejection
| |
| | |
| T<sub>A</sub> - temperature during heat addition
| |
|
| |
|
| T<sub>R</sub> - temperature during heat rejection
| | {{Image|ESC31.gif|right|261px|Figure 1: Carnot cycle schematic diagram}} |
| | Figure 1 contains a Carnot cycle schematic diagram. Air enters a compressor at point 1, and exits the compressor at point 2. Isentropic compression is considered with no entropy change. Air enters a heat exchanger -- heat addition -- at point 2, and exits the heat exchanger at point 3. At a constant temperature, heat addition takes place. Air enters a turbine at point 3, and exits the turbine at point 4. Isentropic expansion is considered with no entropy change. Air enters a heat exchanger -- heat rejection -- at point 4, and exits the heat exchanger at point 1. At a constant temperature, heat rejection takes place. It should be mentioned that air at point 1 enters the compressor and the cycle is repeated. |
|
| |
|
| T<sub>1</sub> - compressor inlet temperature
| | Figure 2 presents a temperature versus entropy of the Carnot cycle. The thermal efficiency of the cycle can be expressed as a function of the specific external work (i.e., specific net power output) and the added heat to the working fluid as follows: |
|
| |
|
| T<sub>2</sub> - compressor outlet temperature
| | <math>\eta = \frac{w}{q_\mathrm h} = \frac{w_\mathrm t - w_\mathrm c}{q_\mathrm h} = \frac{q_\mathrm h - q_\mathrm l}{q_\mathrm h} = 1 - \frac{q_\mathrm l}{q_\mathrm h} = 1 - \frac{T_\mathrm 1\Delta s}{T_\mathrm 2\Delta s} = 1 - \frac{T_\mathrm 1}{T_\mathrm 2}</math> |
|
| |
|
| T<sub>3</sub> - turbine inlet temperature
| | and <math>1 - \frac{T_\mathrm 1}{T_\mathrm 2} = 1 - \frac{T_\mathrm R}{T_\mathrm A}</math> |
|
| |
|
| T<sub>4</sub> - turbine outlet temperature
| | {{Image|ESC32.gif|right|189px|Figure 2: Temperature-Entropy diagram of carnot cycle}} |
|
| |
|
| m - working fluid mass flow rate [kg/s]
| | '''η''' is thermal efficiency, '''w''' is specific external work (i.e., specific net power output) [kJ/kg], '''w<sub>t</sub>''' is expansion specific power output [kJ/kg], '''w<sub>c</sub>'''is compression specific power input [kJ/kg], '''q<sub>h</sub>''' is heat added to the working fluid [kJ/kg], '''q<sub>l</sub>''' is heat rejected from the working fluid [kJ/kg], '''Δs''' is entropy change during heat addition and heat rejection, '''T<sub>A</sub>''' is temperature during heat addition, '''T<sub>R</sub>''' is temperature during heat rejection, '''T<sub>1</sub>''' is compressor inlet temperature, '''T<sub>2</sub>''' is compressor outlet temperature, '''T<sub>3</sub>''' is turbine inlet temperature and '''T<sub>4</sub>''' is turbine outlet temperature. |
|
| |
|
| For isentropic compressor and turbine | | For the isentropic compressor and turbine: |
|
| |
|
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| | <math>\kappa = c_p / c_v</math> and <math>\kappa</math> is 1.4 for air |
|
| |
|
| and | | and |
|
| |
|
| T<sub>2</sub>/T<sub>1</sub> = (p<sub>2</sub>/p<sub>1</sub>)<sup>(ϰ-1)/ϰ</sup> = T<sub>3</sub>/T<sub>4</sub> = (p<sub>3</sub>/p<sub>4</sub>)<sup>(ϰ-1)/ϰ</sup>
| | <math>T_\mathrm2 / T_\mathrm1 = (p_\mathrm2 / p_\mathrm1)^{(\kappa - 1) / \kappa} = T_\mathrm3 / T_\mathrm4 = (p_\mathrm3 / p_\mathrm4)^{(\kappa - 1) / \kappa}</math> |
| | |
| Again, it follows that
| |
| | |
| η = 1 - T<sub>1</sub>/T<sub>2</sub> = 1 - T<sub>R</sub>/T<sub>A</sub>
| |
| | |
| The Carnot cycle efficiency is not dependant on the working fluid properties.
| |
|
| |
|
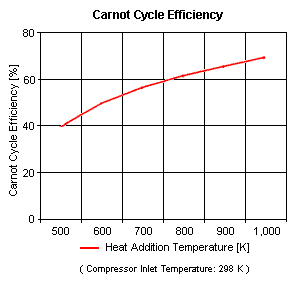
| Figure 3 presents the Carnot cycle efficiency as a function of the heat addition temperature. It should be noted that the compressor inlet temperature is at standard ambient conditions of 298 [K] and 1 [atm] of absolute pressure.
| | Again, it follows that: |
| [[Image:ESC33.gif|center]]
| |
| <center>Figure 3 - Carnot Cycle Efficiency vs Heat Addition Temperature</center>
| |
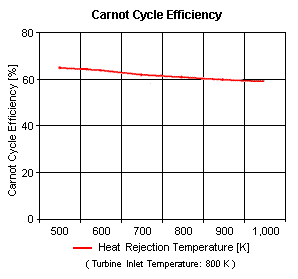
| Figure 4 presents the Carnot cycle efficiency as a function of the heat rejection temperature. It should be noted that the turbine inlet temperature is at 800 [K].
| |
| [[Image:ESC34.gif|center]]
| |
| <center>Figure 4 - Carnot Cycle Efficiency vs Heat Rejection Temperature</center>
| |
| One can notice that the Carnot cycle efficiency increases with an increase in the heat addition temperature when the heat rejection temperature does not change at all. One can notice that the Carnot cycle efficiency decreases with an increase in the heat rejection temperature when the heat addition temperature does not change at all.
| |
|
| |
|
| The general assumptions are as follows:
| | <math>\eta = 1 - \frac{T_\mathrm 1}{T_\mathrm 2} = 1 - \frac{T_\mathrm R}{T_\mathrm A}</math> |
|
| |
|
| Working fluid is air. There is no friction. Compression and expansion are isentropic -- there is no entropy change. During heat addition and heat rejection, the air temperature does not change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| | Thus, we see that the Carnot cycle efficiency is not dependant on the working fluid properties. It is dependent only on the inlet and outlet temperatures. |
|
| |
|
| The governing equations are as follows:
| | {{Image|ESC33.gif|right|299px|Figure 3: Carnot Cycle Efficiency vs Heat Addition Temperature}} |
|
| |
|
| T<sub>2</sub>/T<sub>1</sub> = (p<sub>2</sub>/p<sub>1</sub>)<sup>(ϰ-1)/ϰ</sup>
| | {{Image|ESC34.gif|right|298px|Figure 4: Carnot Cycle Efficiency vs Heat Rejection Temperature}} |
|
| |
|
| T<sub>3</sub>/T<sub>4</sub> = (p<sub>3</sub>/p<sub>4</sub>)<sup>(ϰ-1)/ϰ</sup>
| | Figure 3 presents the Carnot cycle efficiency as a function of the heat addition temperature (with the compressor inlet temperature at ambient conditions of 298 [[K]] and 1 [[atm]] of absolute pressure). |
|
| |
|
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| | Figure 4 presents the Carnot cycle efficiency as a function of the heat rejection temperature (with the turbine inlet temperature at 800 K. |
|
| |
|
| pv = RT
| | It can be shown that the Carnot cycle efficiency increases with an increase in the heat addition temperature when the heat rejection temperature is constant, and the cycle efficiency decreases with an increase in the heat rejection temperature when the heat addition temperature is constant. To do so, the general assumptions are: |
|
| |
|
| η = 1 - T<sub>1</sub>/T<sub>2</sub> = 1 - T<sub>R</sub>/T<sub>A</sub>
| | :The working fluid is air, there is no friction, the compression and expansion are isentropic, the air temperature does not change during the heat addition and heat rejection, the air behaves as an ideal gas (i.e., pv = RT) and the specific heat is constant. |
|
| |
|
| Input data are as follows:
| | The governing equations are: |
|
| |
|
| T<sub>1</sub> = 298 [K]
| | <math>\frac{T_\mathrm 2}{T_\mathrm 1} = \left(\frac{p_\mathrm 2}{p_\mathrm 1}\right)^{(\kappa - 1) / \kappa}</math> |
|
| |
|
| p<sub>1</sub> = 1 [atm]
| | <math>\frac{T_\mathrm 3}{T_\mathrm 4} = \left(\frac{p_\mathrm 3}{p_\mathrm 4}\right)^{(\kappa - 1) / \kappa}</math> |
|
| |
|
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| | <math>\eta = 1 - \frac{T_\mathrm 1}{T_\mathrm 2} = 1 - \frac{T_\mathrm R}{T_\mathrm A}</math> |
|
| |
|
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| | The input data are: '''T<sub>1</sub>''' = 298 K, '''p<sub>1</sub>''' = 1 atm and '''k''' is 1.4 for air. The results are shown in Tables 1 and 2: |
|
| |
|
| The results are as follows:
| | {| class="wikitable" align = left |
| {| class="wikitable" align = center | | |+Table 1: Carnot Cycle Efficiency<br> |
| |+Table 1 - Carnot Cycle Efficiency vs Heat Addition Temperature | | vs Heat Addition Temperature<br> |
| Heat Rejection Temperature is 298 [K]
| | (with heat rejection at 298 K) |
| |- | | |- |
| !Heat Addition Temperature | | !Heat Addition<br>Temperature, K |
| [K]
| | !Cycle Efficiency, % |
| !Carnot Cycle Efficiency | |
| [%]
| |
| |- | | |- |
| |<center>500</center> | | |<center>500</center> |
| Line 126: |
Line 86: |
| |<center>70</center> | | |<center>70</center> |
| |} | | |} |
| | |
| {| class="wikitable" align = center | | {| class="wikitable" align = center |
| |+Table 2 - Carnot Cycle Efficiency vs Heat Rejection Temperature | | |+Table 2 - Carnot Cycle Efficiency<br> |
| Heat Addition Temperature is 800 [K]
| | vs Heat Rejection Temperature<br> |
| | (with heat addition at 800 K) |
| |- | | |- |
| !Heat Rejection Temperature | | !Heat Rejection<br>Temperature, K |
| [K]
| | !Cycle Efficiency, % |
| !Carnot Cycle Efficiency | |
| [%]
| |
| |- | | |- |
| |<center>278</center> | | |<center>278</center> |
| Line 156: |
Line 116: |
| |<center>59</center> | | |<center>59</center> |
| |} | | |} |
| The Carnot cycle efficiency increases with an increase in the heat addition temperature when the heat rejection temperature does not change at all. Furthermore, the Carnot cycle efficiency decreases with an increase in the heat rejection temperature when the heat addition temperature does not change at all.
| |
|
| |
| The Carnot cycle efficiency is not dependant on the working fluid properties.
| |
|
| |
| ===Brayton cycle===
| |
|
| |
| In the presented Brayton cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| A gas turbine is a heat engine that uses a high temperature, high pressure gas as the working fluid. Combustion of a fuel in air is usually used to produce the needed temperatures and pressures in the gas turbine, which is why gas turbines are often referred to as combustion turbines. Expansion of the high temperature, high pressure working fluid takes place in the gas turbine. The gas turbine shaft rotation drives an electric generator and a compressor for the working fluid, air, used in the gas turbine combustor. Many gas turbines also use a heat exchanger called a recouperator to impart turbine exhaust heat into the combustor's air/fuel mixture. Gas turbines produce high quality heat that can be used to generate steam for combined heat and power and combined-cycle applications, significantly enhancing efficiency.
| |
|
| |
| The initial state of the working fluid, air, is assumed to be at point 1 at the atmospheric conditions, 298 [K] temperature and 1 [atm] pressure. The working fluid is compressed, isentropically, along line 1-2 by a compressor and enters the combustor. At a constant pressure, combustion takes place, fuel is added to the combustor and the working fluid temperature raises. High temperature working fluid exits the combustor at point 3. Then the working fluid enters a gas turbine where an isentropic expansion occurs, producing power. The working fluid exits the gas turbine at point 4. It should be mentioned that the working fluid at point 1 enters the compressor and the cycle is repeated.
| |
|
| |
| A schematic layout of the ideal, open Brayton cycle is shown in Figure 1.
| |
| [[Image:ESC35.gif|center]]
| |
| <center>Figure 1 - Brayton Cycle Schematic Layout</center>
| |
| The changes in the state of the working fluid, air, are presented in a T - s diagram in Figure 2.
| |
| [[Image:ESC36.gif|center]]
| |
| <center>Figure 2 - Brayton Cycle Temperature vs Entropy Diagram</center>
| |
| It should be pointed out that this material deals with the open Brayton cycle. The way how the T - s diagram is presented, it describes a closed Brayton cycle -- this would require a heat exchanger after point 4 where the working fluid would be cooled down to point 1 and the cycle repeats. Therefore, the T - s diagram is presented as a closed Brayton cycle to allow easier understanding and derivation of the Brayton cycle thermal efficiency -- heat addition and heat rejection.
| |
|
| |
| The gas turbine and compressor are connected by shaft so the considerable amount of work done on the gas turbine is used to power the compressor.
| |
|
| |
| It can be noticed from the T - s diagram that the work done on the gas turbine is greater than the work necessary to power the compressor -- constant pressure lines in the T - s diagram diverge by going to the right side (entropy wise).
| |
|
| |
| The thermal cycle efficiency can be given as a function of specific external work (specific net power output) and added heat to the working fluid as follows:
| |
|
| |
| η = w/q<sub>h</sub> = (w<sub>t</sub> - w<sub>c</sub>)/q<sub>h</sub> = (q<sub>h</sub> - q<sub>l</sub>)/q<sub>h</sub>
| |
|
| |
| or
| |
|
| |
| η = 1 - q<sub>l</sub>/q<sub>h</sub> = 1 - (c<sub>p</sub>(T<sub>4</sub> - T<sub>1</sub>))/(c<sub>p</sub>(T<sub>3</sub> - T<sub>2</sub>)) = 1 - (T<sub>1</sub>(T<sub>4</sub>/T<sub>1</sub> - 1))/(T<sub>2</sub>(T<sub>3</sub>/T<sub>2</sub> - 1))
| |
|
| |
| where
| |
|
| |
| η - thermal efficiency [/]
| |
|
| |
| w - specific external work (specific net power output) [kJ/kg]
| |
|
| |
| w<sub>t</sub> - expansion specific power output [kJ/kg]
| |
|
| |
| w<sub>c</sub> - compression specific power input [kJ/kg]
| |
|
| |
| W<sub>t</sub> - expansion power output [kW]
| |
|
| |
| W<sub>c</sub> - compression power input [kW]
| |
|
| |
| q<sub>h</sub> - added heat to the working fluid [kJ/kg]
| |
|
| |
| q<sub>l</sub> - heat rejected from the working fluid [kJ/kg]
| |
|
| |
| c<sub>p</sub> - specific heat at constant pressure [kJ/kg*K]
| |
|
| |
| c<sub>v</sub> - specific heat at constant volume [kJ/kg*K]
| |
|
| |
| m - working fluid mass flow rate [kg/s]
| |
|
| |
| For isentropic turbine and compressor
| |
|
| |
| p<sub>3</sub>/p<sub>4</sub> = (T<sub>3</sub>/T<sub>4</sub>)<sup>ϰ/(ϰ-1)</sup>
| |
|
| |
| p<sub>2</sub>/p<sub>1</sub> = (T<sub>2</sub>/T<sub>1</sub>)<sup>ϰ/(ϰ-1)</sup>
| |
|
| |
| Knowing that
| |
|
| |
| p<sub>3</sub>/p<sub>4</sub> = p<sub>2</sub>/p<sub>1</sub>
| |
|
| |
| where
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| p<sub>1</sub>, p<sub>2</sub>, p<sub>3</sub>, p<sub>4</sub> - pressure values at points 1, 2, 3 and 4 [atm]
| |
|
| |
| T<sub>1</sub>, T<sub>2</sub>, T<sub>3</sub>, T<sub>4</sub> - temperature values at points 1, 2, 3 and 4 [K]
| |
|
| |
| It follows that
| |
|
| |
| T<sub>3</sub>/T<sub>4</sub> = T<sub>2</sub>/T<sub>1</sub>
| |
|
| |
| or
| |
|
| |
| T<sub>3</sub>/T<sub>2</sub> = T<sub>4</sub>/T<sub>1</sub>
| |
|
| |
| Therefore, after some mathematical operations the thermal efficiency is:
| |
|
| |
| η = 1 - T<sub>1</sub>/T<sub>2</sub> = 1 - T<sub>4</sub>/T<sub>3</sub>
| |
|
| |
| If the temperature ratio is substituted in terms of the pressure ratio:
| |
|
| |
| η = 1 - 1/r<sub>p</sub><sup>(ϰ-1)/ϰ</sup>
| |
|
| |
| where
| |
|
| |
| r<sub>p</sub> - pressure ratio p<sub>2</sub>/p<sub>1</sub> [/]
| |
|
| |
| The derived Brayton cycle thermal efficiency depends on the pressure ratio and on the working fluid. In Figure 3, it is shown the thermal efficiency increases with the pressure ratio. In this material, air is the only working fluid analyzed. However, it can be concluded that the thermal efficiency increases with the higher value for ϰ, which is a ratio of gas specific heat values (cp/cv).
| |
| [[Image:ESC37.gif|center]]
| |
| <center>Figure 3 - Brayton Cycle Efficiency</center>
| |
| Here, two general performance trends are considered. First, impact of the gas turbine inlet temperature and compressor pressure ratio on the Brayton cycle specific power output and second, impact of the working mass flow rate on the Brayton cycle power output.
| |
|
| |
| Figure 4 presents the results of the first performance trend, while Figure 5 presents the results of the second trend.
| |
| [[Image:ESC38.gif|center]]
| |
| <center>Figure 4 - Brayton Cycle Specific Power Output</center>
| |
| [[Image:ESC39.gif|center]]
| |
| <center>Figure 5 - Brayton Cycle Power Output</center>
| |
| One can notice that the Brayton cycle specific power output increases with an increase in the gas turbine inlet temperature. Furthermore, the increase is higher for the higher compressor pressure ratio.
| |
|
| |
| One can notice that the Brayton cycle power output increases with an increase in the working fluid mass flow rate. The increase is higher for the higher compressor pressure ratio.
| |
|
| |
| The general assumptions are as follows:
| |
|
| |
| Compression and expansion processes are reversible and adiabatic – isentropic. The working fluid has the same composition throughout the cycle. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| p<sub>3</sub>/p<sub>4</sub> = (T<sub>3</sub>/T<sub>4</sub>)<sup>ϰ/(ϰ-1)</sup>
| |
|
| |
| p<sub>2</sub>/p<sub>1</sub> = (T<sub>2</sub>/T<sub>1</sub>)<sup>ϰ/(ϰ-1)</sup>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| w<sub>c</sub> = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)
| |
|
| |
| W<sub>c</sub> = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)m
| |
|
| |
| w<sub>t</sub> = c<sub>p</sub>(T<sub>3</sub> - T<sub>4</sub>)
| |
|
| |
| W<sub>t</sub> = c<sub>p</sub>(T<sub>3</sub> - T<sub>4</sub>)m
| |
|
| |
| η = 1 - 1/r<sub>p</sub><sup>(ϰ-1)/ϰ</sup>
| |
|
| |
| r<sub>p</sub> = p<sub>2</sub>/p<sub>1</sub>
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 298 [K]
| |
|
| |
| p<sub>1</sub> = 1 [atm]
| |
|
| |
| T<sub>3</sub> = 900, 1,200 and 1,500 [K]
| |
|
| |
| p<sub>3</sub> = 5 and 15 [atm]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| m = 50, 100 and 150 [kg/s]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Brayton Cycle Efficiency vs Pressure Ratio
| |
| |-
| |
| !Pressure Ratio
| |
| [/]
| |
| !Efficiency
| |
| [%]
| |
| |-
| |
| |<center>5</center>
| |
| |<center>36.92</center>
| |
| |-
| |
| |<center>10</center>
| |
| |<center>48.22</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>53.87</center>
| |
| |-
| |
| |<center>20</center>
| |
| |<center>57.53</center>
| |
| |-
| |
| |<center>25</center>
| |
| |<center>60.16</center>
| |
| |}
| |
| {| class="wikitable" align = center
| |
| |+Table 2 - Specific Power Output vs Pressure Ratio
| |
| for a few Gas Turbine Inlet Values
| |
| |-
| |
| !Specific Power Output
| |
| [kW/kg/s]
| |
| !colspan="3" |Gas Turbine Inlet Temperature
| |
| [K]
| |
| |-
| |
| !Pressure Ratio
| |
| [/]
| |
| !900
| |
| !1,200
| |
| !1,500
| |
| |-
| |
| |<center>5</center>
| |
| |<center>159</center>
| |
| |<center>270</center>
| |
| |<center>381</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>137</center>
| |
| |<center>300</center>
| |
| |<center>462</center>
| |
| |}
| |
|
| |
| {| class="wikitable" align = center
| |
| |+Table 3 - Power Output vs Pressure Ratio
| |
| for a few Mass Flow Rates
| |
| |-
| |
| !Power Output
| |
| [MW]
| |
| !colspan="3" |Mass Flow Rate
| |
| [kg/s]
| |
| |-
| |
| !Pressure Ratio
| |
| [/]
| |
| !50
| |
| !100
| |
| !150
| |
| |-
| |
| |<center>5</center>
| |
| |<center>19.1</center>
| |
| |<center>38.1</center>
| |
| |<center>57.2</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>23.1</center>
| |
| |<center>46.2</center>
| |
| |<center>69.3</center>
| |
| |}
| |
| The Brayton cycle thermal efficiency depends on the pressure ratio and on the working fluid. The thermal efficiency increases with the pressure ratio. Also, the thermal efficiency increases with the higher value for ϰ, which is a ratio of gas specific heat values (c<sub>p</sub>/c<sub>v</sub>).
| |
|
| |
| The Brayton cycle specific power output increases with an increase in the gas turbine inlet temperature. Furthermore, the increase is higher for the higher compressor pressure ratio.
| |
|
| |
| The Brayton cycle power output increases with an increase in the working fluid mass flow rate. The increase is higher for the higher compressor pressure ratio.
| |
|
| |
| ===Otto cycle===
| |
|
| |
| In the presented Otto cycle analysis, only air is considered as the working fluid behaving as the perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| Figure 1 contains an Otto cycle pressure vs volume diagram. Air enters a cylinder at point 1 when compression starts, and compression ends at point 2. Isentropic compression is considered with no entropy change. Heat addition starts at point 2, and heat addition ends at point 3. At a constant volume, air gets heated and the working fluid temperature raises. Expansion starts at point 3, and expansion ends at point 4. Isentropic expansion is considered with no entropy change. Air heat rejection starts at point 4, and heat rejection ends at point 1. At a constant volume, air gets cooled and the working fluid temperature goes down. It should be mentioned that air at point 1 enters the compression process again and the cycle is repeated.
| |
| [[Image:ESC310.gif|center]]
| |
| <center>Figure 1 - Otto Cycle Pressure vs Volume Diagram</center>
| |
| Figure 2 presents an Otto Cycle entropy vs temperature diagram.
| |
| [[Image:ESC311.gif|center]]
| |
| <center>Figure 2 - Otto Cycle Temperature vs Entropy Diagram</center>
| |
| The thermal cycle efficiency can be given as a function of specific external work (specific net power output) and added heat to the working fluid as follows:
| |
|
| |
| η = w/q<sub>h</sub> = (w<sub>e</sub> - w<sub>c</sub>)/q<sub>h</sub> = (q<sub>h</sub> - q<sub>l</sub>)/q<sub>h</sub>
| |
|
| |
| or
| |
|
| |
| η = 1 - q<sub>l</sub>/q<sub>h</sub> = 1 - (c<sub>v</sub>(T<sub>4</sub> - T<sub>1</sub>))/(c<sub>v</sub>(T<sub>3</sub> - T<sub>2</sub>)) = 1 - (T<sub>1</sub>(T<sub>4</sub>/T<sub>1</sub> - 1))/(T<sub>2</sub>(T<sub>3</sub>/T<sub>2</sub> - 1))
| |
|
| |
| where
| |
|
| |
| η - thermal efficiency [/]
| |
|
| |
| w - specific external work (specific net power output) [kJ/kg]
| |
|
| |
| w<sub>e</sub> - expansion specific power output [kJ/kg]
| |
|
| |
| w<sub>c</sub> - compression specific power input [kJ/kg]
| |
|
| |
| W<sub>e</sub> - expansion power output [kW]
| |
|
| |
| W<sub>c</sub> - compression power input [kW]
| |
|
| |
| q<sub>h</sub> - added heat to the working fluid [kJ/kg]
| |
|
| |
| q<sub>l</sub> - heat rejected from the working fluid [kJ/kg]
| |
|
| |
| c<sub>p</sub> - specific heat at constant pressure [kJ/kg*K]
| |
|
| |
| c<sub>v</sub> - specific heat at constant volume [kJ/kg*K]
| |
|
| |
| m - working fluid mass flow rate [kg/s]
| |
|
| |
| For isentropic compression and expansion
| |
|
| |
| T<sub>2</sub>/T<sub>1</sub> = (p<sub>2</sub>/p<sub>1</sub>)<sup>(ϰ-1)/ϰ</sup> = (V<sub>1/</sub>V<sub>2</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| T<sub>4</sub>T<sub>3</sub> = (p<sub>4</sub>/p<sub>3</sub>)<sup>(ϰ-1)/ϰ</sup> = (V<sub>3</sub>/V<sub>4</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| Knowing that
| |
|
| |
| p<sub>3</sub>/p<sub>4</sub> = p<sub>2</sub>/p<sub>1</sub>
| |
|
| |
| where
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| p<sub>1</sub>, p<sub>2</sub>, p<sub>3</sub>, p<sub>4</sub> - pressure values at points 1, 2, 3 and 4 [atm]
| |
|
| |
| T<sub>1</sub>, T<sub>2</sub>, T<sub>3</sub>, T<sub>4</sub> - temperature values at points 1, 2, 3 and 4 [K]
| |
|
| |
| It follows that
| |
|
| |
| T<sub>3</sub>/T<sub>4</sub> = T<sub>2</sub>/T<sub>1</sub> = (V<sub>1</sub>/V<sub>2</sub>)<sup>(ϰ-1)</sup> = ε<sup>(ϰ-1)</sup>
| |
|
| |
| where
| |
|
| |
| ε = V<sub>1</sub>/V<sub>2</sub>
| |
|
| |
| Therefore, after some mathematical operations the thermal efficiency is:
| |
|
| |
| η = 1 - T<sub>1</sub>/T<sub>2</sub> = 1 - 1/(V<sub>1</sub>/V<sub>2</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| If the temperature ratio is substituted in terms of the volume/compression ratio:
| |
|
| |
| η = 1 - 1/<sub>ε</sub><sup>(ϰ-1)</sup>
| |
|
| |
| Figure 3 presents the Otto cycle efficiency as a function of the compression ratio. It should be noted that the compressor inlet temperature is at standard ambient conditions of 298 [K] and 1 [atm] of absolute pressure. Final combustion temperature is 1,500 [K].
| |
| [[Image:ESC312.gif|center]]
| |
| <center>Figure 3 - Otto Cycle Efficiency vs Compression Ratio</center>
| |
| Figure 4 presents the Otto cycle power output as a function of combustion temperature and compression ratio. It should be noted that the number of revolutions is 60 [1/s] for a given geometry of a four cylinder and four stroke Otto engine.
| |
| [[Image:ESC313.gif|center]]
| |
| <center>Figure 4 - Otto Cycle Power Output</center>
| |
| One can notice that the Otto cycle efficiency increases with an increase in the compression ratio. One can notice that the Otto cycle power output increases with an increase in the combustion temperature and that the Otto cycle power output is greater for lower compression ratio values.
| |
|
| |
| The general assumptions are as follows:
| |
|
| |
| Working fluid is air. There is no friction. Compression and expansion are isentropic -- there is no entropy change. During heat addition and heat rejection, the air temperature does change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| T<sub>2</sub>/T<sub>1</sub> = (V<sub>1</sub>/V<sub>2</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| T<sub>3</sub>/T<sub>4</sub> = (V<sub>4</sub>/V<sub>3</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| w<sub>c</sub> = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)
| |
|
| |
| W<sub>c</sub> = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)m
| |
|
| |
| w<sub>e</sub> = c<sub>p</sub>(T<sub>3</sub> - T<sub>4</sub>)
| |
|
| |
| W<sub>e</sub> = c<sub>p</sub>(T<sub>3</sub> - T<sub>4</sub>)m
| |
|
| |
| η = 1 - 1/ε<sup>(ϰ -1)</sup>
| |
|
| |
| ε = V<sub>1</sub>/V<sub>2</sub>
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 298 [K]
| |
|
| |
| p<sub>1</sub> = 1 [atm]
| |
|
| |
| T<sub>3</sub> = 900, 1,200 and 1,500 [K]
| |
|
| |
| ε = 5, 10 and 15 [/]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Otto Cycle Efficiency vs Compression Ratio
| |
| |-
| |
| !Compression
| |
| Ratio
| |
| [/]
| |
| !Otto Cycle Efficiency
| |
| [%]
| |
| |-
| |
| |<center>2.5</center>
| |
| |<center>30.7</center>
| |
| |-
| |
| |<center>5</center>
| |
| |<center>47.5</center>
| |
| |-
| |
| |<center>7.5</center>
| |
| |<center>55.3</center>
| |
| |-
| |
| |<center>10</center>
| |
| |<center>60.2</center>
| |
| |-
| |
| |<center>12.5</center>
| |
| |<center>63.6</center>
| |
| |}
| |
| {| class="wikitable" align = center
| |
| |+Table 2 - Otto Cycle Power Output
| |
| |-
| |
| !Power Output
| |
| [kW]
| |
| !colspan="3" |Combustion Temperature
| |
| [K]
| |
| |-
| |
| !Compression Ratio
| |
| [/]
| |
| !900
| |
| !1,200
| |
| !1,500
| |
| |-
| |
| |<center>5</center>
| |
| |<center>123.0</center>
| |
| |<center>233.9</center>
| |
| |<center>344.9</center>
| |
| |-
| |
| |<center>10</center>
| |
| |<center>71.0</center>
| |
| |<center>211.7</center>
| |
| |<center>352.3</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>10.1</center>
| |
| |<center>164.7</center>
| |
| |<center>319.3</center>
| |
| |}
| |
| The Otto cycle efficiency increases with an increase in the compression ratio. Also, the Otto cycle power output increases with an increase in the combustion temperature and the Otto cycle power output is greater for lower compression ratio values.
| |
|
| |
| ===Diesel cycle===
| |
|
| |
| In the presented Diesel cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| Figure 1 contains a Diesel cycle pressure vs volume diagram. Air enters a cylinder at point 1 when compression starts, and compression ends at point 2. Isentropic compression is considered with no entropy change. Heat addition starts at point 2, and heat addition ends at point 3. At a constant pressure, air gets heated and the working fluid temperature raises. Expansion starts at point 3, and expansion ends at point 4. Isentropic expansion is considered with no entropy change. Air heat rejection starts at point 4, and heat rejection ends at point 1. At a constant volume, air gets cooled and the working fluid temperature goes down. It should be mentioned that air at point 1 enters the compression process again and the cycle is repeated.
| |
| [[Image:ESC314.gif|center]]
| |
| <center>Figure 1 - Diesel Cycle Pressure vs Volume Diagram</center>
| |
| Figure 2 presents a Diesel Cycle entropy vs temperature diagram.
| |
| [[Image:ESC315.gif|center]]
| |
| <center>Figure 2 - Diesel Cycle Temperature vs Entropy Diagram</center>
| |
| The thermal cycle efficiency can be given as a function of specific external work (specific net power output) and added heat to the working fluid as follows:
| |
|
| |
| The thermal cycle efficiency can be given as a function of specific external work (specific net power output) and added heat to the working fluid as follows:
| |
|
| |
| η = w/q<sub>h</sub> = (w<sub>e</sub> - w<sub>c</sub>)/q<sub>h</sub> = (q<sub>h</sub> - q<sub>l</sub>)/q<sub>h</sub>
| |
|
| |
| or
| |
|
| |
| η = 1 - q<sub>l</sub>/q<sub>h</sub> = 1 - (c<sub>v</sub>(T<sub>4</sub> - T<sub>1</sub>))/(c<sub>p</sub>(T<sub>3</sub> - T<sub>2</sub>)) = 1 - (T<sub>1</sub>(T<sub>4</sub>/T<sub>1</sub> - 1))/(ϰT<sub>2</sub>(T<sub>3</sub>/T<sub>2</sub> - 1))
| |
|
| |
| where
| |
|
| |
| η - thermal efficiency [/]
| |
|
| |
| w - specific external work (specific net power output) [kJ/kg]
| |
|
| |
| w<sub>e</sub> - expansion specific power output [kJ/kg]
| |
|
| |
| w<sub>c</sub> - compression specific power input [kJ/kg]
| |
|
| |
| W<sub>e</sub> - expansion power output [kW]
| |
|
| |
| W<sub>c</sub> - compression power input [kW]
| |
|
| |
| q<sub>h</sub> - added heat to the working fluid [kJ/kg]
| |
|
| |
| q<sub>l</sub> - heat rejected from the working fluid [kJ/kg]
| |
|
| |
| c<sub>p</sub> - specific heat at constant pressure [kJ/kg*K]
| |
|
| |
| c<sub>v</sub> - specific heat at constant volume [kJ/kg*K]
| |
|
| |
| m - working fluid mass flow rate [kg/s]
| |
|
| |
| For isentropic turbine and compressor
| |
|
| |
| T<sub>2</sub>/T<sub>1</sub> = (p<sub>2</sub>/p<sub>1</sub>)<sup>(ϰ-1)/ϰ</sup> = (V<sub>1</sub>/V<sub>2</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| T<sub>4</sub>/T<sub>3</sub> = (p<sub>4</sub>/p<sub>3</sub>)<sup>(ϰ-1)/ϰ</sup> = (V<sub>3</sub>/V<sub>4</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| Knowing that
| |
|
| |
| p<sub>3</sub>/p<sub>4</sub> = p<sub>2</sub>/p<sub>1</sub>
| |
|
| |
| where
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| p<sub>1</sub>, p<sub>2</sub>, p<sub>3</sub>, p<sub>4</sub> - pressure values at points 1, 2, 3 and 4 [atm]
| |
|
| |
| T<sub>1</sub>, T<sub>2</sub>, T<sub>3</sub>, T<sub>4</sub> - temperature values at points 1, 2, 3 and 4 [K]
| |
|
| |
| Knowing that
| |
|
| |
| s<sub>3</sub> - s<sub>2</sub> = s<sub>4</sub> - s<sub>1</sub>
| |
|
| |
| and
| |
|
| |
| s<sub>3</sub> - s<sub>2</sub> = c<sub>p</sub>ln(T<sub>3</sub>/T<sub>2</sub>)
| |
|
| |
| s<sub>4</sub> - s<sub>1</sub> = c<sub>v</sub>ln(T<sub>4</sub>/T<sub>1</sub>)
| |
|
| |
| It follows
| |
|
| |
| (T<sub>3</sub>/T<sub>2</sub>)<sup>ϰ</sup> = T<sub>4</sub>/T<sub>1</sub>
| |
|
| |
| It follows that
| |
|
| |
| T<sub>3</sub>/T<sub>4</sub> = T<sub>2</sub>/T<sub>1</sub> = (V<sub>1</sub>/V<sub>2</sub>)<sup>(ϰ-1)</sup> = ε<sup>(ϰ-1)</sup>
| |
|
| |
| where
| |
|
| |
| ε = V<sub>1</sub>/V<sub>2</sub>
| |
|
| |
| φ = V<sub>3</sub>/V<sub>2</sub>
| |
|
| |
| Therefore, after some mathematical operations the thermal efficiency is:
| |
|
| |
| η = 1 - (T<sub>1</sub>((T<sub>3</sub>/T<sub>2</sub>)<sup>ϰ</sup> - 1)))/(ϰT<sub>2</sub>(T<sub>3</sub>/T<sub>2</sub> - 1))
| |
|
| |
| If the temperature ratio is substituted in terms of the volume/compression ratio:
| |
|
| |
| η = 1 - (φ<sup>ϰ</sup> - 1)/(ϰε<sup>(ϰ-1)</sup>(φ – 1))
| |
|
| |
| Figure 3 presents the Diesel cycle efficiency as a function of the compression ratio. It should be noted that the compressor inlet temperature is at standard ambient conditions of 298 [K] and 1 [atm] of absolute pressure. The cut off ratio is 3 [/].
| |
| [[Image:ESC316.gif|center]]
| |
| <center>Figure 3 - Diesel Cycle Efficiency vs Compression Ratio</center>
| |
| Figure 4 presents the Diesel Cycle power output as a function of compression and cut off ratio values. It should be noted that the number of revolutions is 60 [1/s] for a given geometry of a four cylinder and four stroke Diesel engine.
| |
| [[Image:ESC317.gif|center]]
| |
| <center>Figure 4 - Diesel Cycle Power Output</center>
| |
| One can notice that the Diesel cycle efficiency increases with an increase in the compression ratio. One can notice that the Diesel Cycle power output increases with an increase in the compression ratio and that the Diesel cycle power output is greater for higher cut off ratio values.
| |
|
| |
| The general assumptions are as follows:
| |
|
| |
| Working fluid is air. There is no friction. Compression and expansion are isentropic -- there is no entropy change. During heat addition and heat rejection, the air temperature does change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| T<sub>2</sub>/T<sub>1</sub> = (V<sub>1</sub>/V<sub>2</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| T<sub>3</sub>/T<sub>4</sub> = (V<sub>4</sub>/V<sub>3</sub>)<sup>(ϰ-1)</sup>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| w<sub>c</sub> = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)
| |
|
| |
| W<sub>c</sub> = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)m
| |
|
| |
| w<sub>e</sub> = c<sub>p</sub>(T<sub>3</sub> - T<sub>2</sub>) + c<sub>p</sub> - T4)
| |
|
| |
| W<sub>e</sub> = c<sub>p</sub>(T<sub>3</sub> - T<sub>2</sub>)m + c<sub>p</sub>(T<sub>3</sub> - T<sub>4</sub>)m
| |
|
| |
| η = 1 - (φ<sup>(ϰ–1)</sup>)/(ϰε<sup>(ϰ-1)</sup>(φ - 1))
| |
|
| |
| ε = V<sub>1</sub>/V<sub>2</sub>
| |
|
| |
| φ = V<sub>3</sub>/V<sub>2</sub>
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 298 [K]
| |
|
| |
| p<sub>1</sub> = 1 [atm]
| |
|
| |
| ε = 5, 7.5, 10, 12.5 and 15 [/]
| |
|
| |
| φ = 3 and 4 [/]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Diesel Cycle Efficiency vs Compression Ratio
| |
| |-
| |
| !Compression
| |
| Ratio
| |
| [/]
| |
| !Diesel Cycle Efficiency
| |
| [%]
| |
| |-
| |
| |<center>5</center>
| |
| |<center>31.4</center>
| |
| |-
| |
| |<center>7.5</center>
| |
| |<center>41.7</center>
| |
| |-
| |
| |<center>10</center>
| |
| |<center>48.0</center>
| |
| |-
| |
| |<center>12.5</center>
| |
| |<center>52.5</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>55.8</center>
| |
| |}
| |
| {| class="wikitable" align = center
| |
| |+Table 2 - Diesel Cycle Power Output
| |
| |-
| |
| !Power Output
| |
| [kW]
| |
| !colspan="5" |Compression Ratio
| |
| [/]
| |
| |-
| |
| !Cut Off Ratio
| |
| [/]
| |
| !5
| |
| !7.5
| |
| !10
| |
| !12.5
| |
| !15
| |
| |-
| |
| |<center>3</center>
| |
| |<center>919.0</center>
| |
| |<center>1,230.2</center>
| |
| |<center>1,438.7</center>
| |
| |<center>1,701.4</center>
| |
| |<center>1,894.4</center>
| |
| |-
| |
| |<center>4</center>
| |
| |<center>1,266.8</center>
| |
| |<center>1,733.6</center>
| |
| |<center>2,113.9</center>
| |
| |<center>2,440.5</center>
| |
| |<center>2,729.9</center>
| |
| |}
| |
| The Diesel cycle efficiency increases with an increase in the compression ratio. Also, the Diesel cycle power output increases with an increase in the compression ratio and the Diesel cycle power output is greater for higher cut off ratio values.
| |
|
| |
| ==Power cycle components/processes analysis==
| |
|
| |
| In this section dealing with power cycle components/processes, ideal compression, combustion and expansion operation and their preformance trends are presented.
| |
|
| |
| ===Compression===
| |
|
| |
| In the presented compression analysis, only air is considered as the working fluid behaving as the perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| Figure 1 contains a compression schematic layout. Air enters a compressor at point 1, and exits the compressor at point 2. Isentropic compression is considered with no entropy change.
| |
| [[Image:ESC41.gif|center]]
| |
| <center>Figure 1 - Compression Schematic Layout</center>
| |
| Figure 2 presents a compression entropy vs temperature diagram.
| |
| [[Image:ESC42.gif|center]]
| |
| <center>Figure 2 - Compression Temperature vs Entropy Diagram</center>
| |
| Figure 3 presents compression specific power input requirements for a few typical pressure ratio values. It should be noted that the air enters the compressor at standard ambient conditions of 298 [K] and 1 [atm] of absolute pressure.
| |
| [[Image:ESC43.gif|center]]
| |
| <center>Figure 3 - Compression Specific Power Input</center>
| |
| Figure 4 presents compression power input requirements for two typical pressure ratio values and a few different air mass flow rate values.
| |
| [[Image:ESC44.gif|center]]
| |
| <center>Figure 4 - Compression Power Input</center>
| |
| One can notice that both compression specific power input and power input increase with the pressure ratio. As the air mass flow increases, the compression power input requirements increase too.
| |
|
| |
| The general assumptions are as follows:
| |
|
| |
| Working fluid is air. There is no friction and heat transfer. Compression is isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| T<sub>2</sub>/T<sub>1</sub> = (p<sub>2</sub>/p<sub>1</sub>)<sup>(ϰ-1)/ϰ</sup>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| w = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)
| |
|
| |
| W = c<sub>p</sub>(T<sub>2</sub> - T<sub>1</sub>)m
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 298 [K]
| |
|
| |
| p<sub>1</sub> = 1 [atm]
| |
|
| |
| p<sub>2</sub> = 5, 10 and 15 [atm]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| m = 50, 100 and 150 [kg/s]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Specific Power Input vs Pressure Ratio
| |
| |-
| |
| !Pressure Ratio
| |
| [/]
| |
| !Specific Power Input
| |
| [kW/kg/s]
| |
| |-
| |
| |<center>5</center>
| |
| |<center>174</center>
| |
| |-
| |
| |<center>10</center>
| |
| |<center>278</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>349</center>
| |
| |}
| |
| {| class="wikitable" align = center
| |
| |+Table 2 - Power Input vs Pressure Ratio for a few Mass Flow Rates
| |
| |-
| |
| !Power Input
| |
| [MW]
| |
| !colspan="3" |Mass Flow Rate
| |
| [kg/s]
| |
| |-
| |
| !Pressure Ratio
| |
| [/]
| |
| !50
| |
| !100
| |
| !150
| |
| |-
| |
| |<center>5</center>
| |
| |<center>8.68</center>
| |
| |<center>17.37</center>
| |
| |<center>26.06</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>17.47</center>
| |
| |<center>34.94</center>
| |
| |<center>52.41</center>
| |
| |}
| |
| Both compression specific power input and power input increase with the pressure ratio. As the air mass flow increases, the compression power input requirements increase too.
| |
|
| |
| ===Combustion===
| |
|
| |
| A combustion analysis for a few typical fuel cases (carbon, hydrogen, sulfur, coal, oil and gas) when the fuel reacts with air at stoichiometric conditions is presented.
| |
|
| |
| Furthermore, in the presented combustion analysis, both fuel and air are at standard inlet combustion conditions of 298 [K] and 1 [atm] of absolute pressure. Furthermore, combustion is complete and with no heat loss.
| |
|
| |
| During the combustion, a large amount of reactants' chemical energy gets released in the form of thermal energy.
| |
|
| |
| Enthalpy of combustion (HHV) is the difference between the reactants enthalpy value minus the combustion products enthalpy value at the standard reference temperature, which is 298 [K].
| |
|
| |
| When the reactants enthalpy value is equal to the combustion products enthalpy value, one can calculate the combustion products flame temperature (adiabatic temperature).
| |
|
| |
| The plot in Figure 1 depicts the reactants and combustion products enthalpy value change with an increase in the temperature.
| |
| [[Image:ESC45.gif|center]]
| |
| <center>Figure 1 - Reactants and Combustion Products Enthalpy vs Temperature</center>
| |
| Physical properties for both reactants and combustion products are very important and need to be known in order to carry out successful combustion calculations.
| |
|
| |
| The plot in Figure 2 depicts how the reactants and combustion products species enthalpy values change with the temperature. The physical properties provided in this plot come from the JANAF Thermochemical Data - Tables, 1970.
| |
| [[Image:ESC46.gif|center]]
| |
| <center>Figure 2 - Reactants and Combustion Products Species Enthalpy vs Temperature</center>
| |
|
| |
| It is interesting to note that the enthalpy value for basic combustion elements such as carbon (C), hydrogen (H<sub>2</sub>), sulfur (S), oxygen (O<sub>2</sub>) and nitrogen (N<sub>2</sub>) is equal to zero at the standard combustion conditions of 298 [K] and 1 [atm].
| |
|
| |
| Also, it should be mentioned that for ideal gas species, the enthalpy value is only dependent on the temperature.
| |
|
| |
| In addition to knowing the reactants and combustion products physical properties, for any kind of combustion analysis and calculations, it is important to know both fuel and oxidant compositions.
| |
|
| |
| For solid and liquid type fuels, the fuel composition is given on the weight basis for a unit mass amount. For the gas type fuels, the fuel composition is provided on the mole/volume basis for a unit volume amount. In this analysis, methane (CH<sub>4</sub>) is the only gas fuel considered. In order to keep the combustion analysis simple and straightforward, the CH<sub>4</sub> composition is provided on the weight basis. Oxidant composition is usually given on the mole/volume basis.
| |
|
| |
| Table 1 provides the fuel composition.
| |
| {| class="wikitable" align = center
| |
| |+ Table 1: Fuel Composition (Proportion by Mass)
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! C
| |
| ! H
| |
| ! S
| |
| ! N
| |
| ! O
| |
| ! H<sub>2</sub>O
| |
| ! CH<sub>4</sub>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | 1.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | 0.000
| |
| | 1.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | 0.000
| |
| | 0.000
| |
| | 1.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Coal</center>
| |
| | 0.780
| |
| | 0.050
| |
| | 0.030
| |
| | 0.040
| |
| | 0.080
| |
| | 0.020
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Oil</center>
| |
| | 0.860
| |
| | 0.140
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Gas</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | 1.000
| |
| |}
| |
| Table 2 provides the standard air composition.
| |
| {| class="wikitable" align = center
| |
| |+ Table 2: Oxidant/Air Composition
| |
| |-
| |
| ! <center>Oxidant</center>
| |
| ! N<br/>[kg/kg]
| |
| ! O<br/>[kg/kg]
| |
| ! N<sub>2</sub><br/>[kmol/kmol]
| |
| ! O<sub>2</sub><br/>[kmol/kmol]
| |
| |-
| |
| | <center>Air</center>
| |
| | <center>0.767</center>
| |
| | <center>0.233</center>
| |
| | <center>0.790</center>
| |
| | <center>0.210</center>
| |
| |}
| |
| Again, in this combustion analysis, only the stoichiometric combustion is analyzed. Results of such analysis are provided, including a combustion products composition on weight and mole/volume basis, a flame temperature, a stoichiometric ratio and a higher heating value (HHV).
| |
|
| |
| Table 3 provides the combustion products composition on the weight basis.
| |
| {| class="wikitable" align = center
| |
| |+ Table 3: Combustion Products on Weight Basis (Proportion by Mass)
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! CO<sub>2</sub>
| |
| ! H<sub>2</sub>O
| |
| ! SO<sub>2</sub>
| |
| ! N<sub>2</sub>
| |
| ! O<sub>2</sub>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | 0.295
| |
| | 0.000
| |
| | 0.000
| |
| | 0.705
| |
| | 0.000
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | 0.000
| |
| | 0.255
| |
| | 0.000
| |
| | 0.745
| |
| | 0.000
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | 0.000
| |
| | 0.000
| |
| | 0.378
| |
| | 0.622
| |
| | 0.000
| |
| |-
| |
| | <center>Coal</center>
| |
| | 0.249
| |
| | 0.041
| |
| | 0.005
| |
| | 0.705
| |
| | 0.000
| |
| |-
| |
| | <center>Oil</center>
| |
| | 0.203
| |
| | 0.079
| |
| | 0.000
| |
| | 0.718
| |
| | 0.000
| |
| |-
| |
| | <center>Gas</center>
| |
| | 0.151
| |
| | 0.124
| |
| | 0.000
| |
| | 0.725
| |
| | 0.000
| |
| |}
| |
| Table 4 provides the combustion products composition on the volume basis.
| |
| {| class="wikitable" align = center
| |
| |+ Table 4: Combustion Products on Mole Basis (Proportion by Moles [kmol])
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! CO<sub>2</sub>
| |
| ! H<sub>2</sub>O
| |
| ! SO<sub>2</sub>
| |
| ! N<sub>2</sub>
| |
| ! O<sub>2</sub>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | 0.210
| |
| | 0.000
| |
| | 0.000
| |
| | 0.790
| |
| | 0.000
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | 0.000
| |
| | 0.347
| |
| | 0.000
| |
| | 0.653
| |
| | 0.000
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | 0.000
| |
| | 0.000
| |
| | 0.210
| |
| | 0.789
| |
| | 0.000
| |
| |-
| |
| | <center>Coal</center>
| |
| | 0.170
| |
| | 0.068
| |
| | 0.002
| |
| | 0.759
| |
| | 0.000
| |
| |-
| |
| | <center>Oil</center>
| |
| | 0.133
| |
| | 0.127
| |
| | 0.000
| |
| | 0.740
| |
| | 0.000
| |
| |-
| |
| | <center>Gas</center>
| |
| | 0.095
| |
| | 0.190
| |
| | 0.000
| |
| | 0.715
| |
| | 0.000
| |
| |}
| |
| When considering coal, oil and gas as the fuel, coal has the largest amount of CO<sub>2</sub> in the combustion products on both weight and mole basis.
| |
|
| |
| Table 5 provides the combustion products flame temperature, stoichiometric ratio and the fuel higher heating value.
| |
| {| class="wikitable"
| |
| |+ Table 5: Other Fuel Characteristics
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! <center>Flame Temperature<br/>[K]</center>
| |
| ! <center>Stoichiometric Ratio<br/>(See Note Below!)</center>
| |
| ! <center>HHV<br/>[kJ/kg]</center>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | <center>2,460</center>
| |
| | <center>11.444</center>
| |
| | <center>32,779.8</center>
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | <center>2,525</center>
| |
| | <center>34.333</center>
| |
| | <center>141,866.8</center>
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | <center>1,972</center>
| |
| | <center>4.292</center>
| |
| | <center>9,261.3</center>
| |
| |-
| |
| | <center>Coal</center>
| |
| | <center>2,484</center>
| |
| | <center>10.487</center>
| |
| | <center>32,937.9</center>
| |
| |-
| |
| | <center>Oil</center>
| |
| | <center>2,484</center>
| |
| | <center>14.580</center>
| |
| | <center>47,630.0</center>
| |
| |-
| |
| | <center>Gas</center>
| |
| | <center>2,327</center>
| |
| | <center>17.167</center>
| |
| | <center>50,151.2</center>
| |
| |-
| |
| |colspan=4 align="left"|Note: Stoichiometric ratio is the mass of air required for complete combustion of a unit mass of fuel. Thus, 1 [kg] of carbon fuel requires 11.444 [kg] of air for complete, ideal combustion.
| |
| |}
| |
| Stoichiometric ratio is the mass of air required for complete combustion of a unit mass of fuel. Thus, 1 [kg] of carbon fuel requires 11.433 [kg] of air for complete, ideal combustion.
| |
|
| |
| Today, global warming is becoming more evident and it is being said that it is primarily caused by CO<sub>2</sub> emissions. A detailed combustion analysis, as it is provided here, can be very useful in determining different fuel and technology scenarios that would result in the reduction of current CO<sub>2</sub> emissions.
| |
|
| |
| The general assumptions:
| |
|
| |
| Both fuel and air are at standard inlet combustion conditions of 298 [K] and 1 [atm] of absolute pressure.
| |
|
| |
| Furthermore, combustion is complete and with no heat loss.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| Enthalpy of combustion (HHV) is the difference between the reactants enthalpy value minus the combustion products enthalpy value at the standard reference temperature, which is 298 [K].
| |
|
| |
| When the reactants enthalpy value is equal to the combustion products enthalpy value, one can calculate the combustion products flame temperature (adiabatic temperature).
| |
|
| |
| Input data are as follows:
| |
| {| class="wikitable" align = center
| |
| |+ Table 1: Fuel Composition (Proportion by Mass)
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! C
| |
| ! H
| |
| ! S
| |
| ! N
| |
| ! O
| |
| ! H<sub>2</sub>O
| |
| ! CH<sub>4</sub>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | 1.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | 0.000
| |
| | 1.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | 0.000
| |
| | 0.000
| |
| | 1.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Coal</center>
| |
| | 0.780
| |
| | 0.050
| |
| | 0.030
| |
| | 0.040
| |
| | 0.080
| |
| | 0.020
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Oil</center>
| |
| | 0.860
| |
| | 0.140
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | 0.000
| |
| | <center>-</center>
| |
| |-
| |
| | <center>Gas</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | <center>-</center>
| |
| | 1.000
| |
| |}
| |
| {| class="wikitable" align = center
| |
| |+ Table 2: Oxidant/Air Composition
| |
| |-
| |
| ! <center>Oxidant</center>
| |
| ! N<br/>[kg/kg]
| |
| ! O<br/>[kg/kg]
| |
| ! N<sub>2</sub><br/>[kmol/kmol]
| |
| ! O<sub>2</sub><br/>[kmol/kmol]
| |
| |-
| |
| | <center>Air</center>
| |
| | <center>0.767</center>
| |
| | <center>0.233</center>
| |
| | <center>0.790</center>
| |
| | <center>0.210</center>
| |
| |}
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+ Table 3: Combustion Products on Weight Basis (Proportion by Mass)
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! CO<sub>2</sub>
| |
| ! H<sub>2</sub>O
| |
| ! SO<sub>2</sub>
| |
| ! N<sub>2</sub>
| |
| ! O<sub>2</sub>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | 0.295
| |
| | 0.000
| |
| | 0.000
| |
| | 0.705
| |
| | 0.000
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | 0.000
| |
| | 0.255
| |
| | 0.000
| |
| | 0.745
| |
| | 0.000
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | 0.000
| |
| | 0.000
| |
| | 0.378
| |
| | 0.622
| |
| | 0.000
| |
| |-
| |
| | <center>Coal</center>
| |
| | 0.249
| |
| | 0.041
| |
| | 0.005
| |
| | 0.705
| |
| | 0.000
| |
| |-
| |
| | <center>Oil</center>
| |
| | 0.203
| |
| | 0.079
| |
| | 0.000
| |
| | 0.718
| |
| | 0.000
| |
| |-
| |
| | <center>Gas</center>
| |
| | 0.151
| |
| | 0.124
| |
| | 0.000
| |
| | 0.725
| |
| | 0.000
| |
| |}
| |
| {| class="wikitable" align = center
| |
| |+ Table 4: Combustion Products on Mole Basis (Proportion by Moles [kmol])
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! CO<sub>2</sub>
| |
| ! H<sub>2</sub>O
| |
| ! SO<sub>2</sub>
| |
| ! N<sub>2</sub>
| |
| ! O<sub>2</sub>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | 0.210
| |
| | 0.000
| |
| | 0.000
| |
| | 0.790
| |
| | 0.000
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | 0.000
| |
| | 0.347
| |
| | 0.000
| |
| | 0.653
| |
| | 0.000
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | 0.000
| |
| | 0.000
| |
| | 0.210
| |
| | 0.789
| |
| | 0.000
| |
| |-
| |
| | <center>Coal</center>
| |
| | 0.170
| |
| | 0.068
| |
| | 0.002
| |
| | 0.759
| |
| | 0.000
| |
| |-
| |
| | <center>Oil</center>
| |
| | 0.133
| |
| | 0.127
| |
| | 0.000
| |
| | 0.740
| |
| | 0.000
| |
| |-
| |
| | <center>Gas</center>
| |
| | 0.095
| |
| | 0.190
| |
| | 0.000
| |
| | 0.715
| |
| | 0.000
| |
| |}
| |
| {| class="wikitable"
| |
| |+ Table 5: Other Fuel Characteristics
| |
| |-
| |
| ! <center>Fuel</center>
| |
| ! <center>Flame Temperature<br/>[K]</center>
| |
| ! <center>Stoichiometric Ratio<br/>(See Note Below!)</center>
| |
| ! <center>HHV<br/>[kJ/kg]</center>
| |
| |-
| |
| | <center>Carbon</center>
| |
| | <center>2,460</center>
| |
| | <center>11.444</center>
| |
| | <center>32,779.8</center>
| |
| |-
| |
| | <center>Hydrogen</center>
| |
| | <center>2,525</center>
| |
| | <center>34.333</center>
| |
| | <center>141,866.8</center>
| |
| |-
| |
| | <center>Sulfur</center>
| |
| | <center>1,972</center>
| |
| | <center>4.292</center>
| |
| | <center>9,261.3</center>
| |
| |-
| |
| | <center>Coal</center>
| |
| | <center>2,484</center>
| |
| | <center>10.487</center>
| |
| | <center>32,937.9</center>
| |
| |-
| |
| | <center>Oil</center>
| |
| | <center>2,484</center>
| |
| | <center>14.580</center>
| |
| | <center>47,630.0</center>
| |
| |-
| |
| | <center>Gas</center>
| |
| | <center>2,327</center>
| |
| | <center>17.167</center>
| |
| | <center>50,151.2</center>
| |
| |-
| |
| |colspan=4 align="left"|Note: Stoichiometric ratio is the mass of air required for complete combustion of a unit mass of fuel. Thus, 1 [kg] of carbon fuel requires 11.444 [kg] of air for complete, ideal combustion.
| |
| |}
| |
|
| |
| ===Expansion===
| |
|
| |
| In the presented expansion analysis, only air is considered as the working fluid behaving as the perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| Figure 1 contains an expansion schematic layout. Air enters a turbine at point 1, and exits the turbine at point 2. Isentropic expansion is considered with no entropy change.
| |
| [[Image:ESC47.gif|center]]
| |
| <center>Figure 1 - Expansion Schematic Layout</center>
| |
| Figure 2 presents an expansion entropy vs temperature diagram.
| |
| [[Image:ESC48.gif|center]]
| |
| <center>Figure 2 - Expansion Temperature vs Entropy Diagram</center>
| |
| Figure 3 presents expansion specific power output values for a few typical pressure ratio values. It should be noted that the air enters the turbine at the temperature of 1,500 [K] and the turbine exhaust pressure is always equal to the standard ambient pressure -- 1 [atm] of absolute pressure.
| |
| [[Image:ESC49.gif|center]]
| |
| <center>Figure 3 - Expansion Specific Power Output</center>
| |
| Figure 4 presents expansion power output values for two typical pressure ratio values and a few different air mass flow rate values.
| |
| [[Image:ESC410.gif|center]]
| |
| <center>Figure 4 - Expansion Power Output</center>
| |
| One can notice that both expansion specific power output and power output increase with the pressure ratio. As the air mass flow increases, the expansion power output values increase too.
| |
|
| |
| The general assumptions are as follows:
| |
|
| |
| Working fluid is air. There is no friction and heat transfer. Expansion is isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| T<sub>1</sub>/T<sub>2</sub> = (p<sub>1</sub>/p<sub>2</sub>)<sup>(ϰ-1)/ϰ</sup>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| w = c<sub>p</sub>(T<sub>1</sub> - T<sub>2</sub>)
| |
|
| |
| W = c<sub>p</sub>(T<sub>1</sub> - T<sub>2</sub>)m
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 1,500 [K]
| |
|
| |
| p<sub>1</sub> = 5, 10 and 15 [atm]
| |
|
| |
| p<sub>2</sub> = 1 [atm]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| m = 50, 100 and 150 [kg/s]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Specific Power Output vs Pressure Ratio
| |
| |-
| |
| !Pressure Ratio
| |
| [/]
| |
| !Specific Power Output
| |
| [kW/kg/s]
| |
| |-
| |
| |<center>5</center>
| |
| |<center>555</center>
| |
| |-
| |
| |<center>10</center>
| |
| |<center>726</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>811</center>
| |
| |}
| |
| {| class="wikitable" align = center
| |
| |+Table 2 - Power Output vs Pressure Ratio for a few Mass Flow Rates
| |
| |-
| |
| !Power Output
| |
| [MW]
| |
| !colspan="3" |Mass Flow Rate
| |
| [kg/s]
| |
| |-
| |
| !Pressure Ratio
| |
| [/]
| |
| !50
| |
| !100
| |
| !150
| |
| |-
| |
| |<center>5</center>
| |
| |<center>27.76</center>
| |
| |<center>55.51</center>
| |
| |<center>83.27</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>40.56</center>
| |
| |<center>81.13</center>
| |
| |<center>121.69</center>
| |
| |}
| |
| Both expansion specific power output and power output increase with the pressure ratio. As the air mass flow increases, the expansion power output values increase too.
| |
|
| |
| ==Compressible flow analysis==
| |
|
| |
| In this section dealing with compressible flow, ideal and isentropic operation of nozzle, diffuser and thrust and their preformance trends are presented.
| |
|
| |
| ===Nozzle===
| |
|
| |
| In the presented nozzle analysis, only air is considered as the working fluid behaving as the perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| Figure 1 contains a nozzle schematic layout. Air enters a nozzle at point 1, and exits the nozzle at point 2. Isentropic expansion is considered with no entropy change.
| |
| [[Image:ESC51.gif|center]]
| |
| <center>Figure 1: Nozzle Schematic Layout</center>
| |
| Figure 2 presents a nozzle entropy vs temperature diagram.
| |
| [[Image:ESC52.gif|center]]
| |
| <center>Figure 2 - Nozzle Temperature vs Entropy Diagram</center>
| |
| Figure 3 presents nozzle performance -- stagnation over static temperature and pressure values -- as a function of the Mach Number. Only subsonic nozzle operation is considered. It should be noted that air enters the nozzle at the stagnation conditions of 1,500 [K] and 10 [atm] of absolute pressure.
| |
| [[Image:ESC53.gif|center]]
| |
| <center>Figure 3 - Nozzle Performance vs Mach Number</center>
| |
| One can notice that nozzle stagnation over static temperature and pressure ratio values increase with an increase of the Mach Number.
| |
|
| |
| The general assumptions are as follows:
| |
|
| |
| Working fluid is air. There is no friction and heat transfer. Expansion is isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| T<sub>t</sub> /T = (1 + M<sup>2</sup>(ϰ - 1)/2)
| |
|
| |
| p<sub>t</sub>/p = (1 + M<sup>2</sup>(ϰ - 1)/2)<sup>ϰ/(ϰ-1)</sup>
| |
|
| |
| T<sub>t</sub>/T = (p<sub>t</sub>/p)<sup>(ϰ-1)/ϰ</sup>
| |
|
| |
| v = (2c<sub>p</sub>(T<sub>t</sub> - T)<sup>)1/2</sup>
| |
|
| |
| v<sub>s</sub> = (ϰRT)<sup>1/2</sup>
| |
|
| |
| M = v/v<sub>s</sub>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 1,500 [K]
| |
|
| |
| p<sub>1</sub> = 10 [atm]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| M = 0.39, 0.67 and 1 [/]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Nozzle Performance vs Mach Number
| |
| |-
| |
| !Mach Number
| |
| [/]
| |
| !Temperature Ratio
| |
| [/]
| |
| !Pressure Ratio
| |
| [/]
| |
| |-
| |
| |<center>0.39</center>
| |
| |<center>1.03</center>
| |
| |<center>1.11</center>
| |
| |-
| |
| |<center>0.67</center>
| |
| |<center>1.09</center>
| |
| |<center>1.35</center>
| |
| |-
| |
| |<center>1.00</center>
| |
| |<center>1.19</center>
| |
| |<center>1.86</center>
| |
| |}
| |
| Nozzle stagnation over static temperature and pressure ratio values increase with an increase of the Mach Number.
| |
|
| |
| ===Diffuser===
| |
|
| |
| In the presented diffuser analysis, only air is considered as the working fluid behaving as the perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| Figure 1 contains a diffuser schematic layout. Air enters a diffuser at point 1, and exits the diffuser at point 2. Working fluid inlet velocity gets reduced to zero resulting in the stagnation temperature and pressure increase. Isentropic process is considered with no entropy change.
| |
| [[Image:ESC54.gif|center]]
| |
| <center>Figure 1 - Diffuser Schematic Layout</center>
| |
| Figure 2 presents a diffuser entropy vs temperature diagram.
| |
| [[Image:ESC55.gif|center]]
| |
| <center>Figure 2 - Diffuser Temperature vs Entropy Diagram</center>
| |
| Figure 3 presents diffuser performance -- stagnation over static temperature and pressure values -- as a function of the Mach Number. Only subsonic diffuser operation is considered. It should be noted that the air enters the diffuser at the static conditions of 298 [K] and 1 [atm] of absolute pressure.
| |
| [[Image:ESC56.gif|center]]
| |
| <center>Figure 3 - Diffuser Performance vs Mach Number</center>
| |
| One can notice that diffuser stagnation over static temperature and pressure ratio values increase with an increase of the Mach Number.
| |
|
| |
| The genaral assumptions are as follows:
| |
|
| |
| Working fluid is air. There is no friction and heat transfer. Isentropic process -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| T<sub>t</sub>/T = (1 + M<sup>2</sup>(ϰ - 1)/2)
| |
|
| |
| p<sub>t</sub>/p = (1 + M<sup>2</sup>(ϰ - 1)/2)<sup>ϰ/(ϰ-1)</sup>
| |
|
| |
| T<sub>t</sub>/T = (p<sub>t</sub>/p)<sup>(ϰ-1)/ϰ</sup>
| |
|
| |
| T<sub>t</sub> = T + v<sup>2</sup>/(2c<sub>p</sub>)
| |
|
| |
| v<sub>s</sub> = (ϰRT)<sup>1/2</sup>
| |
|
| |
| M = v/v<sub>s</sub>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 298 [K]
| |
|
| |
| p<sub>1</sub> = 1 [atm]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| M = 0.29, 0.58 and 0.95 [/]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Diffuser Performance vs Mach Number
| |
| |-
| |
| !Mach Number
| |
| [/]
| |
| !Temperature Ratio
| |
| [/]
| |
| !Pressure Ratio
| |
| [/]
| |
| |-
| |
| |<center>0.29</center>
| |
| |<center>1.017</center>
| |
| |<center>1.06</center>
| |
| |-
| |
| |<center>0.58</center>
| |
| |<center>1.067</center>
| |
| |<center>1.25</center>
| |
| |-
| |
| |<center>0.95</center>
| |
| |<center>1.182</center>
| |
| |<center>1.80</center>
| |
| |}
| |
| Diffuser stagnation over static temperature and pressure ratio values increase with an increase of the Mach Number.
| |
| ===Thrust===
| |
|
| |
| In the presented thrust analysis, only air is considered as the working fluid behaving as the perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
| |
|
| |
| Figure 1 contains a thrust schematic layout. Air enters a nozzle at point 1, and exits the nozzle at point 2. Isentropic expansion is considered with no entropy change.
| |
| [[Image:ESC57.gif|center]]
| |
| <center>Figure 1 - Thrust Schematic Layout</center>
| |
| Figure 2 presents a thrust entropy vs temperature diagram.
| |
| [[Image:ESC58.gif|center]]
| |
| <center>Figure 2 - Thrust Temperature vs Entropy Diagram</center>
| |
| Figure 3 presents thrust performance as a function of the nozzle inlet stagnation temperature and pressure for a few fixed values such as: working fluid mass flow rate, nozzle outlet Mach Number and ambient pressure. Only subsonic nozzle operation is considered.
| |
| [[Image:ESC59.gif|center]]
| |
| <center>Figure 3 - Thrust Performance vs Inlet Stagnation Temperature and Pressure</center>
| |
| One can notice that thrust values increase with an increase of the inlet stagnation temperature and pressure.
| |
|
| |
| The general assumptions are as follows:
| |
|
| |
| Working fluid is air. There is no friction and heat transfer. Expansion is isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
| |
|
| |
| The governing equations are as follows:
| |
|
| |
| T<sub>t</sub>/T = (1 + M<sup>2</sup>(ϰ - 1)/2)
| |
|
| |
| p<sub>t</sub>/p = (1 + M<sup>2</sup>(ϰ - 1)/2)<sup>ϰ/(ϰ-1)</sup>
| |
|
| |
| T<sub>t</sub>/T = (p<sub>t</sub>/p)<sup>(ϰ -1)/k</sup>
| |
|
| |
| v = (2c<sub>p</sub>(T<sub>t</sub> – T))<sup>1/2</sup>
| |
|
| |
| v<sub>s</sub> = (ϰRT)<sup>1/2</sup>
| |
|
| |
| M = v/v<sub>s</sub>
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub>
| |
|
| |
| pv = RT
| |
|
| |
| Thrust = vm + (p - p<sub>a</sub>)A
| |
|
| |
| Input data are as follows:
| |
|
| |
| T<sub>1</sub> = 900, 1,200 and 1,500 [K]
| |
|
| |
| p<sub>1</sub> = 5, 10 and 15 [atm]
| |
|
| |
| c<sub>p</sub> = 1.004 [kJ/kg*K]
| |
|
| |
| ϰ = c<sub>p</sub>/c<sub>v</sub> - for air ϰ = 1.4 [/]
| |
|
| |
| m = 1 [kg/s]
| |
|
| |
| M = 0.85 [/]
| |
|
| |
| p<sub>a</sub> = 1 [atm]
| |
|
| |
| The results are as follows:
| |
| {| class="wikitable" align = center
| |
| |+Table 1 - Thrust Performance vs Inlet Stagnation Temperature and Pressure
| |
| |-
| |
| !Thrust
| |
| [N]
| |
| !colspan="3" |Inlet Stagnation Temperature
| |
| [K]
| |
| |-
| |
| !Inlet Stagnation Pressure
| |
| [atm]
| |
| !900
| |
| !1,200
| |
| !1,500
| |
| |-
| |
| |<center>5</center>
| |
| |<center>797.7</center>
| |
| |<center>922.3</center>
| |
| |<center>1,031.1</center>
| |
| |-
| |
| |<center>10</center>
| |
| |<center>873.5</center>
| |
| |<center>1,009.5</center>
| |
| |<center>1,128.6</center>
| |
| |-
| |
| |<center>15</center>
| |
| |<center>898.7</center>
| |
| |<center>1,038.7</center>
| |
| |<center>1,161.3</center>
| |
| |}
| |
| Thrust values increase with an increase of the inlet stagnation temperature and pressure.
| |
|
| |
| ==References==
| |
| <div class="references-small" style="-moz-column-count:2; -webkit-column-count:2; column-count:2;">
| |
| <references />
| |
| </div>
| |
|
| |
| [[Category: CZ Live|CZ Live]]
| |
| [[Category:Engineering Workgroup|Engineering Workgroup]]
| |
| [[Category:Physics Workgroup|Physics Workgroup]]
| |