Polar coordinates: Difference between revisions
imported>Paul Wormer |
mNo edit summary |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
::''For an extension to three dimensions, see [[spherical polar coordinates]].'' | ::''For an extension to three dimensions, see [[spherical polar coordinates]].'' | ||
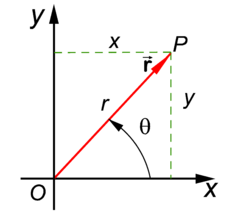
{{Image| Polar coordinates .png|right|250px|Two dimensional polar coordinates ''r'' and θ of vector <math>\scriptstyle \vec{\mathbf{r}}</math>}} | |||
In [[mathematics]] and [[physics]], '''polar coordinates''' are two | In [[mathematics]] and [[physics]], '''polar coordinates''' are two [[number]]s—a [[distance]] and an [[angle]]—that specify the position of a [[point (geometry)|point]] on a [[plane (geometry)|plane]]. | ||
In their classical ("pre-vector") definition | In their classical ("pre-vector") definition, polar coordinates give the position of a point ''P'' with respect to a given point ''O'' (the ''pole'') and a given line (the ''polar axis'') through ''O''. One [[real number]] (''r'' ) gives the distance of ''P'' to ''O'' and another number (θ) gives the angle of the line ''O''—''P'' with the polar axis. Given ''r'' and θ, one determines ''P'' by constructing a [[circle]] of [[radius]] ''r'' with ''O'' as origin, and a line with angle θ measured counterclockwise from the polar axis. The point ''P'' is on the intersection of the circle and the [[line]]. | ||
In modern vector language one identifies the plane with a real Euclidean space <math>\scriptstyle \mathbb{R}^2</math> that has a [[Cartesian coordinate]] system. The crossing of the Cartesian axes | In modern [[vector]] language one identifies the plane with a real [[Euclidean space]] <math>\scriptstyle \mathbb{R}^2</math> that has a [[Cartesian coordinates|Cartesian coordinate]] system. The crossing of the Cartesian axes is on the pole, that is, ''O'' is the origin of the Cartesian system and the polar axis is identified with the ''x''-axis of the Cartesian system. The line ''O''—''P'' is generated by the vector | ||
:<math> | :<math> | ||
\overrightarrow{OP} \equiv \vec{\mathbf{r}}. | \overrightarrow{OP} \equiv \vec{\mathbf{r}}. | ||
| Line 52: | Line 52: | ||
:<math> | :<math> | ||
A = \int_{0}^{2\pi} \int_{0}^R r\, dr\, d\theta = \pi R^2 . | A = \int_{0}^{2\pi} \int_{0}^R r\, dr\, d\theta = \pi R^2 . | ||
</math> | </math>[[Category:Suggestion Bot Tag]] | ||
[[Category: | |||
Latest revision as of 11:00, 5 October 2024
- For an extension to three dimensions, see spherical polar coordinates.
In mathematics and physics, polar coordinates are two numbers—a distance and an angle—that specify the position of a point on a plane.
In their classical ("pre-vector") definition, polar coordinates give the position of a point P with respect to a given point O (the pole) and a given line (the polar axis) through O. One real number (r ) gives the distance of P to O and another number (θ) gives the angle of the line O—P with the polar axis. Given r and θ, one determines P by constructing a circle of radius r with O as origin, and a line with angle θ measured counterclockwise from the polar axis. The point P is on the intersection of the circle and the line.
In modern vector language one identifies the plane with a real Euclidean space that has a Cartesian coordinate system. The crossing of the Cartesian axes is on the pole, that is, O is the origin of the Cartesian system and the polar axis is identified with the x-axis of the Cartesian system. The line O—P is generated by the vector
Hence we obtain the figure on the right where is the position vector of the point P.
Algebraic definition
The polar coordinates r and θ are related to the Cartesian coordinates x and y through
so that for r ≠ 0,
Bounds on the coordinates are: r ≥ 0 and 0 ≤ θ < 3600. Coordinate lines are: the circle (fixed r, all θ) and a half-line from the origin (fixed direction θ all r). The slope of the half-line is tanθ = y/x.
Surface element
The infinitesimal surface element in polar coordinates is
The Jacobian J is the determinant
Example: the area A of a circle of radius R is given by