Rhombus: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>Anthony Argyriou
(create)
 
mNo edit summary
 
(6 intermediate revisions by 3 users not shown)
Line 1: Line 1:
{{subpages}}
{{subpages}}
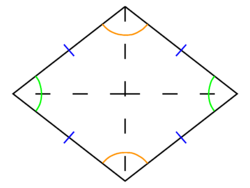
A '''rhombus''' is a [[polygon]] of four sides of equal length.  The angles of each pair of opposite vertices are equal. A rhombus is a special case of a [[parallelogram]] where all four sides are of equal length. A [[square]] is a special case of rhombus, where the all four angles are equal.
{{Image|Rhombus.png|right|250px|A ''rhombus''. All sides (marked blue) are of equal length; opposite angles (same color arc) are equal; diagonals cross at right angles.}}
A '''rhombus''' or '''rhomb''' is a four-sided [[polygon]] (a [[quadrilateral]]) with  sides of equal length.  The angles of each pair of opposite vertices are equal. A rhombus is a special case of a [[parallelogram]], a quadrilateral with equal and parallel opposite sides. A [[square]] is a special case of a rhombus, where all four vertex angles are equal to 90°.


==Properties==
==Properties==
[[Image:Rhombus.png|thumb|right|A '''rhombus''' with some mathematical properties shown]]
As with all quadrilaterals, the sum of the interior angles of a rhombus is 360 degrees; as with a parallelogram, it can be shown that the angles of opposite pairs of vertices are equal.


The perimeter of a rhombus is equal to 4 times the length of one side.  The area of a square is equal to the length of the side multiplied by itself, multiplied by the [[sine]] of the angle between the sides.<ref>Since the sum of the four angles is 360 degrees, and pairs of angles are equal, the sum of the angles of two adjacent vertices is 180 degrees.  Since sin(180-x)=sin(x), the formula produces the same result no matter which vertex angle is chosen.</ref>  <!--The diagonal of a rhombus is ...-->


Any rhombus can [[tile (mathematics)|tile]] a plane with no voids.
As with all quadrilaterals, the sum of the interior angles of a rhombus is 360 degrees;
as with a parallelogram, the angles of opposite pairs of vertices are equal,
and the sum of the angles of two adjacent vertices is 180 degrees.
 
The perimeter of a rhombus is equal to 4 times the length of one side. 
The area of a rhombus is equal to the length of the side multiplied by itself,
multiplied by the [[sine]] of the angle between the sides.
(Since sin(180-x)=sin(x) this does not depend on the choice of the angle.)
 
Any rhombus can [[tile (mathematics)|tile]] a plane with no voids.[[Category:Suggestion Bot Tag]]

Latest revision as of 06:00, 12 October 2024

This article is a stub and thus not approved.
 Main Article
 Discussion
Related Articles  [?]
Bibliography  [?]
External Links  [?]
Citable Version  [?]
 
https://en.citizendium.org/wiki/index.php?title=Rhombus&printable=yes
This editable Main Article is under development and subject to a disclaimer.
PD Image
A rhombus. All sides (marked blue) are of equal length; opposite angles (same color arc) are equal; diagonals cross at right angles.

A rhombus or rhomb is a four-sided polygon (a quadrilateral) with sides of equal length. The angles of each pair of opposite vertices are equal. A rhombus is a special case of a parallelogram, a quadrilateral with equal and parallel opposite sides. A square is a special case of a rhombus, where all four vertex angles are equal to 90°.

Properties

As with all quadrilaterals, the sum of the interior angles of a rhombus is 360 degrees; as with a parallelogram, the angles of opposite pairs of vertices are equal, and the sum of the angles of two adjacent vertices is 180 degrees.

The perimeter of a rhombus is equal to 4 times the length of one side. The area of a rhombus is equal to the length of the side multiplied by itself, multiplied by the sine of the angle between the sides. (Since sin(180-x)=sin(x) this does not depend on the choice of the angle.)

Any rhombus can tile a plane with no voids.

Retrieved from "https://citizendium.org/wiki/index.php?title=Rhombus&oldid=986937"