imported>John R. Brews |
|
| (165 intermediate revisions by one other user not shown) |
| Line 1: |
Line 1: |
| ==Widlar current source==
| | {{AccountNotLive}} |
| [[Image:Widlar Patent.PNG |thumb|350px|Diagram from Widlar's [http://patimg1.uspto.gov/.piw?Docid=03320439&homeurl=http%3A%2F%2Fpatft.uspto.gov%2Fnetacgi%2Fnph-Parser%3FSect1%3DPTO2%2526Sect2%3DHITOFF%2526p%3D1%2526u%3D%25252Fnetahtml%25252FPTO%25252Fsearch-bool.html%2526r%3D16%2526f%3DG%2526l%3D50%2526co1%3DAND%2526d%3DPALL%2526s1%3DWidlar.INNM.%2526OS%3DIN%2FWidlar%2526RS%3DIN%2FWidlar&PageNum=&Rtype=&SectionNum=&idkey=NONE&Input=View+first+page original patent] ]]
| |
| {{TOC|right}} | | {{TOC|right}} |
| A '''Widlar current source''' is a modification of the basic two-[[transistor]] [[current mirror]] that incorporates an emitter degeneration [[resistor]] for only the output transistor, enabling the current source to generate low currents using only moderate resistor values.<ref name=Gray>{{cite book |title=Analysis and design of analog integrated circuits |author=PR Gray, PJ Hurst, SH Lewis & RG Meyer |year=2001 |edition=4rth Edition |publisher=John Wiley and Sons |isbn=0-471-32168-0 |url=http://www.worldcat.org/search?q=0471321680&qt=owc_search |pages= §4.4.1.1 pp. 299–303}}</ref><ref name=Sedra>{{cite book |title=Microelectronic circuits |author=AS Sedra and KC Smith |edition=5th Edition |isbn=0-19-514251-9 |year=2004 |publisher=Oxford University Press |url=http://www.worldcat.org/search?q=0195142519&qt=owc_search |nopp=true |pages=Example 6.14, pp. 654–655 }}</ref><ref name=Rashid>{{cite book |title=Microelectronic circuits: analysis and design |author=MH Rashid |year=1999 |publisher=PWS Publishing Co. |isbn=0-534-95174-0 |url=http://www.worldcat.org/search?q=0534951740&qt=owc_search |pages=661–665}}</ref>
| | [[Image:Current division example.svg|thumbnail|250px|Figure 1: Schematic of an electrical circuit illustrating current division. Notation ''R<sub>T<sub>.</sub></sub>'' refers to the ''total'' resistance of the circuit to the right of resistor ''R<sub>X</sub>''.]] |
|
| |
|
| The Widlar circuit may be used with [[bipolar transistor]]s, [[MOSFET|MOS transistors]], and even [[vacuum tube]]s. An example application is the [[Operational_amplifier#Internal_circuitry_of_741_type_op-amp|741 operational amplifier]],<ref name=Sedra2>{{cite book |title=§9.4.2, p. 899 |author=AS Sedra and KC Smith |edition=5th Edition |isbn=0-19-514251-9 |year=2004 |url=http://www.worldcat.org/search?q=0195142519&qt=owc_search }}</ref> and Widlar used the circuit as a part in many designs.<ref name=journal>See, for example, Figure 2 in [https://www.utdallas.edu/~hellums/docs/JournalPapers/WidlarBandgap.pdf ''IC voltage regulators''].</ref>
| | In [[electronics]], a '''current divider ''' is a simple [[linear]] [[Electrical network|circuit]] that produces an output [[Electric current|current]] (''I''<sub>X</sub>) that is a fraction of its input current (''I''<sub>T</sub>). The splitting of current between the branches of the divider is called '''current division'''. The currents in the various branches of such a circuit divide in such a way as to minimize the total energy expended. |
|
| |
|
| This circuit is named after its inventor, [[Bob Widlar]], and was patented in 1967.<ref name=patent>RJ Widlar: US Patent Number 03320439; Filed May 26, 1965; Granted May 16, 1967: [http://patimg1.uspto.gov/.piw?Docid=03320439&homeurl=http%3A%2F%2Fpatft.uspto.gov%2Fnetacgi%2Fnph-Parser%3FSect1%3DPTO2%2526Sect2%3DHITOFF%2526p%3D1%2526u%3D%25252Fnetahtml%25252FPTO%25252Fsearch-bool.html%2526r%3D16%2526f%3DG%2526l%3D50%2526co1%3DAND%2526d%3DPALL%2526s1%3DWidlar.INNM.%2526OS%3DIN%2FWidlar%2526RS%3DIN%2FWidlar&PageNum=&Rtype=&SectionNum=&idkey=NONE&Input=View+first+page'' Low-value current source for integrated circuits''] </ref><ref name=Linear>See Widlar: [http://scholar.google.com/scholar?as_q=&num=10&btnG=Search+Scholar&as_epq=emitter+degeneration+resistor+&as_oq=&as_eq=&as_occt=any&as_sauthors=Widlar&as_publication=&as_ylo=1965&as_yhi=1975&as_allsubj=all&hl=en&lr= ''Some circuit design techniques for linear integrated circuits''] and [http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=1049994 ''Design techniques for monolithic operational amplifiers'']</ref>
| | The formula describing a current divider is similar in form to that for the [[voltage divider]]. However, the ratio describing current division places the impedance of the unconsidered branches in the [[numerator]], unlike voltage division where the considered impedance is in the numerator. To be specific, if two or more [[Electrical impedance|impedance]]s are in parallel, the current that enters the combination will be split between them in inverse proportion to their impedances (according to [[Ohm's law]]). It also follows that if the impedances have the same value the current is split equally. |
|
| |
|
| ==Analysis== | | ==Resistive divider== |
| [[Image:Widlar Current Source.PNG|thumb|250px|Figure 1: A version of the Widlar current source using bipolar transistors.]]
| | A general formula for the current ''I<sub>X</sub>'' in a resistor ''R<sub>X</sub>'' that is in parallel with a combination of other resistors of total resistance ''R<sub>T</sub>'' is (see Figure 1): |
| Figure 1 is an example Widlar current source using bipolar transistors, where the emitter resistor R<sub>2</sub> is connected to the output transistor Q<sub>2</sub>, and has the effect of reducing the current in Q<sub>2</sub> relative to Q<sub>1</sub>. The key to this circuit is that the voltage drop across the resistor ''R''<sub>2</sub> subtracts from the base-emitter voltage of transistor ''Q''<sub>2</sub>, thereby turning this transistor off compared to transistor ''Q''<sub>1</sub>. This observation is expressed by equating the base voltage expressions found on either side of the circuit in Figure 1 as:
| | :<math>I_X = \frac{R_T}{R_X+R_T}I_T \ </math> |
| | where ''I<sub>T</sub>'' is the total current entering the combined network of ''R<sub>X</sub>'' in parallel with ''R<sub>T</sub>''. Notice that when ''R<sub>T</sub>'' is composed of a [[Series_and_parallel_circuits#Parallel_circuits|parallel combination]] of resistors, say ''R<sub>1</sub>'', ''R<sub>2</sub>'', ... ''etc.'', then the reciprocal of each resistor must be added to find the total resistance ''R<sub>T</sub>'': |
| | :<math> \frac {1}{R_T} = \frac {1} {R_1} + \frac {1} {R_2} + \frac {1}{R_3} + ... \ . </math> |
|
| |
|
| :<math>V_B = V_{BE1} = V_{BE2}+(\beta_2+1)I_{B2}R_2 \ , </math> | | ==General case== |
| | Although the resistive divider is most common, the current divider may be made of frequency dependent [[Electrical impedance|impedance]]s. In the general case the current I<sub>X</sub> is given by: |
| | :<math>I_X = \frac{Z_T} {Z_X+Z_T}I_T \ ,</math> |
|
| |
|
| where β<sub>2</sub> is the beta-value of the output transistor, which is not the same as that of the input transistor, in part because the currents in the two transistors are very different.<ref name=Gray2>{{cite book |title=Figure 2.38, p. 115 |author=PR Gray, PJ Hurst, SH Lewis & RG Meyer |year=2001 |isbn=0-471-32168-0 |url=http://www.worldcat.org/search?q=0471321680&qt=owc_search }}</ref> The variable ''I''<sub>B2</sub> is the base current of the output transistor, ''V''<sub>BE</sub> refers to base-emitter voltage. This equation implies (using the [[Diode_modelling#Shockley_diode_model|Shockley diode law]]):
| | ==Using Admittance== |
| | Instead of using [[Electrical impedance|impedance]]s, the current divider rule can be applied just like the [[voltage divider]] rule if [[admittance]] (the inverse of impedance) is used. |
| | :<math>I_X = \frac{Y_X} {Y_{Total}}I_T</math> |
| | Take care to note that Y<sub>Total</sub> is a straightforward addition, not the sum of the inverses inverted (as you would do for a standard parallel resistive network). For Figure 1, the current I<sub>X</sub> would be |
| | :<math>I_X = \frac{Y_X} {Y_{Total}}I_T = \frac{\frac{1}{R_X}} {\frac{1}{R_X} + \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}I_T</math> |
|
| |
|
| ''Eq. 1''{{anchor|Eq1}}
| | ===Example: RC combination=== |
| :<math>(\beta_2+1)I_{B2} =\left(1 + 1/\beta_2 \right) I_{C2} = \frac{V_{BE1} - V_{BE2}}{R_2} = \frac{V_T}{R_2} \ln \left(\frac {I_{C1}I_{S2}}{I_{C2}I_{S1}}\right)\ , </math> | | [[Image:Low pass RC filter.PNG|thumbnail|220px|Figure 2: A low pass RC current divider]] |
| where ''V''<sub>T</sub> is the [[Boltzmann constant#Role in semiconductor physics: the thermal voltage|thermal voltage]].
| | Figure 2 shows a simple current divider made up of a [[capacitor]] and a resistor. Using the formula above, the current in the resistor is given by: |
|
| |
|
| This equation makes the approximation that the currents are both much larger than the ''scale currents'' ''I''<sub>S1</sub>, ''I''<sub>S2</sub>, an approximation valid except for current levels near [[Bipolar_junction_transistor#Regions_of_operation|cut off]]. In the following the distinction between the two scale currents is dropped, although the difference can be important, for example, if the two transistors are chosen with different areas.
| | ::<math> I_R = \frac {\frac{1}{j \omega C}} {R + \frac{1}{j \omega C} }I_T </math> |
| | :::<math> = \frac {1} {1+j \omega CR} I_T \ , </math> |
| | where ''Z<sub>C</sub> = 1/(jωC) '' is the impedance of the capacitor. |
|
| |
|
| ==Design procedure with specified currents==
| | The product ''τ = CR'' is known as the [[time constant]] of the circuit, and the frequency for which ωCR = 1 is called the [[corner frequency]] of the circuit. Because the capacitor has zero impedance at high frequencies and infinite impedance at low frequencies, the current in the resistor remains at its DC value ''I<sub>T</sub>'' for frequencies up to the corner frequency, whereupon it drops toward zero for higher frequencies as the capacitor effectively [[short-circuit]]s the resistor. In other words, the current divider is a [[low pass filter]] for current in the resistor. |
| To design the mirror, the output current must be related to the two resistor values ''R''<sub>1</sub> and ''R''<sub>2</sub>. A basic observation is that the output transistor is in [[Bipolar_junction_transistor#Regions_of_operation|active mode]] only so long as its collector-base voltage is non-zero. Thus, the simplest bias condition for design of the mirror sets the applied voltage ''V''<sub>A</sub> to equal the base voltage ''V''<sub>B</sub>. This minimum useful value of ''V''<sub>A</sub> is called the ''[[Current mirror#Compliance voltage|compliance voltage]]'' of the current source. With that bias condition, the [[Early effect]] plays no role in the design.<ref name=note1>Of course, one might imagine a design where the output resistance of the mirror is a major consideration. Then a different approach is necessary.</ref>
| |
|
| |
|
| These considerations suggest the following design procedure:
| | ==Loading effect== |
| * Select the desired output current, ''I''<sub>O</sub> = ''I''<sub>C2</sub>.
| | [[Image:Current division.PNG|thumbnail|300px|Figure 3: A current amplifier (gray box) driven by a Norton source (''i<sub>S</sub>'', ''R<sub>S</sub>'') and with a resistor load ''R<sub>L</sub>''. Current divider in blue box at input (''R<sub>S</sub>'',''R<sub>in</sub>'') reduces the current gain, as does the current divider in green box at the output (''R<sub>out</sub>'',''R<sub>L</sub>'')]] |
| * Select the reference current, ''I''<sub>R1</sub>, assumed to be larger than the output current, probably considerably larger. (That is the purpose of the circuit.)
| | The gain of an amplifier generally depends on its source and load terminations. Current amplifiers and transconductance amplifiers are characterized by a short-circuit output condition, and current amplifiers and transresistance amplifiers are characterized using ideal infinite impedance current sources. When an amplifier is terminated by a finite, non-zero termination, and/or driven by a non-ideal source, the effective gain is reduced due to the '''loading effect''' at the output and/or the input, which can be understood in terms of current division. |
| * Determine the input collector current of ''Q''<sub>1</sub>, ''I''<sub>C1</sub>:
| |
| ::<math>I_{C1} = \frac{\beta_1}{\beta_1+1} \left( I_{R1}-I_{C2}/\beta_2 \right)\ . </math>
| |
| * Determine the base voltage ''V''<sub>BE1</sub> using the [[Diode_modelling#Shockley_diode_model|Shockley diode law]]
| |
| ::<math> V_{BE1} = V_T \ln \left(\frac{I_{C1}} {I_S} \right) = V_A\ . </math>
| |
| :where ''I''<sub>S</sub> is a device parameter sometimes called the ''scale current''.
| |
| :The value of base voltage also sets the compliance voltage ''V''<sub>A</sub> = ''V''<sub>BE1</sub>. This voltage is the lowest voltage for which the mirror works properly.
| |
| * Determine ''R''<sub>1</sub>:
| |
| ::<math> R_1 = \frac {V_{CC} - V_A}{I_{R1}}\ . </math>
| |
| {{anchor|R2}}* Determine the emitter leg resistance ''R''<sub>2</sub> using ''[[#Eq1|Eq. 1]]'' (to reduce clutter, the scale currents are chosen equal):
| |
| ::<math>R_2 = \frac{V_T}{\left(1 + 1/\beta_2 \right) I_{C2}} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math>
| |
|
| |
|
| ==Finding the current with given resistor values==
| | Figure 3 shows a current amplifier example. The amplifier (gray box) has input resistance ''R<sub>in</sub>'' and output resistance ''R<sub>out</sub>'' and an ideal current gain ''A<sub>i</sub>''. With an ideal current driver (infinite Norton resistance) all the source current ''i<sub>S</sub>'' becomes input current to the amplifier. However, for a [[Norton's theorem|Norton driver]] a current divider is formed at the input that reduces the input current to |
| The inverse of the design problem is finding the current when the resistor values are known. An iterative method is described next. Assume the current source is biased so the collector-base voltage of the output transistor ''Q''<sub>2</sub> is zero. The current through ''R''<sub>1</sub> is the input or reference current given as, | |
|
| |
|
| :<math>I_{R1} = I_{C1} + I_{B1} + I_{B2} \ </math> | | ::<math>i_{i} = \frac {R_S} {R_S+R_{in}} i_S \ , </math> |
|
| |
|
| ::<math>= I_{C1} + \frac{I_{C1}}{\beta_1} + \frac{I_{C2}}{\beta_2}</math>
| | which clearly is less than ''i<sub>S</sub>''. Likewise, for a short circuit at the output, the amplifier delivers an output current ''i<sub>o</sub>'' = ''A<sub>i</sub> i<sub>i</sub>'' to the short-circuit. However, when the load is a non-zero resistor ''R<sub>L</sub>'', the current delivered to the load is reduced by current division to the value: |
| ::<math> = \frac{V_{CC}-V_{BE1}}{R_1} \ . </math>
| |
| Rearranging, ''I''<sub>C1</sub> is found as:
| |
|
| |
|
| ''Eq. 2''{{anchor|Eq2}}
| | ::<math>i_L = \frac {R_{out}} {R_{out}+R_{L}} A_i i_{i} \ . </math> |
| :<math>I_{C1} =\frac{\beta_1}{\beta_1+1} \left( \frac {V_{CC}-V_{BE1}}{R_1}-\frac{I_{C2}}{\beta_2} \right) </math> | |
|
| |
|
| The diode equation provides:
| | Combining these results, the ideal current gain ''A<sub>i</sub>'' realized with an ideal driver and a short-circuit load is reduced to the '''loaded gain''' ''A<sub>loaded</sub>'': |
|
| |
|
| {{anchor|Eq3}}''Eq. 3''
| | ::<math>A_{loaded} =\frac {i_L} {i_S} = \frac {R_S} {R_S+R_{in}}</math> <math> \frac {R_{out}} {R_{out}+R_{L}} A_i \ . </math> |
| :<math>V_{BE1} = V_T \ln \left( \frac{I_{C1}}{I_{S1}}\right) \ . </math> | |
|
| |
|
| ''[[#Eq1|Eq.1]]'' provides: | | The resistor ratios in the above expression are called the '''loading factors'''. For more discussion of loading in other amplifier types, see [[Voltage division#Loading effect|loading effect]]. |
| :<math>I_{C2} = \frac{V_T}{\left(1 + 1/\beta_2 \right) R_2} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math>
| |
|
| |
|
| These three relations are a nonlinear, implicit determination for the currents that can be solved by iteration.
| | ===Unilateral versus bilateral amplifiers=== |
| * We guess starting values for ''I''<sub>C1</sub> and ''I''<sub>C2</sub>.
| | [[Image:H-parameter current amplifier.PNG|thumbnail|300px|Figure 4: Current amplifier as a bilateral two-port network; feedback through dependent voltage source of gain β V/V]] |
| * We find a value for ''V''<sub>BE1</sub>:
| | Figure 3 and the associated discussion refers to a [[Electronic amplifier#Unilateral or bilateral|unilateral]] amplifier. In a more general case where the amplifier is represented by a [[two-port network|two port]], the input resistance of the amplifier depends on its load, and the output resistance on the source impedance. The loading factors in these cases must employ the true amplifier impedances including these bilateral effects. For example, taking the unilateral current amplifier of Figure 3, the corresponding bilateral two-port network is shown in Figure 4 based upon [[Two-port network#Hybrid parameters (h-parameters)| h-parameters]].<ref name=H_port/> Carrying out the analysis for this circuit, the current gain with feedback ''A<sub>fb</sub>'' is found to be |
| ::<math>V_{BE1} = V_T \ln \left( \frac{I_{C1}}{I_{S1}}\right) \ . </math>
| |
| * We find a new value for ''I''<sub>C1</sub>:
| |
| ::<math>I_{C1} =\frac{\beta_1}{\beta_1+1} \left( \frac {V_{CC}-V_{BE1}}{R_1}-\frac{I_{C2}}{\beta_2} \right) </math>
| |
| *We find a new value for ''I''<sub>C2</sub>:
| |
| ::<math>I_{C2} = \frac{V_T}{\left(1 + 1/\beta_2 \right) R_2} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math>
| |
| This procedure is repeated to convergence, and is set up conveniently in a spreadsheet. One simply uses a macro to copy the new values into the spreadsheet cells holding the initial values to obtain the solution in short order.
| |
|
| |
|
| Note that with the circuit as shown, if V<sub>CC</sub> changes, the output current will change. Hence, to keep the output current constant despite fluctuations in ''V''<sub>CC</sub>, the circuit should be driven by a [[current source|constant current source]] rather than using the resistor ''R''<sub>1</sub>.
| | ::<math> A_{fb} = \frac {i_L}{i_S} = \frac {A_{loaded}} {1+ {\beta}(R_L/R_S) A_{loaded}} \ . </math> |
|
| |
|
| ===Exact solution===
| | That is, the ideal current gain ''A<sub>i</sub>'' is reduced not only by the loading factors, but due to the bilateral nature of the two-port by an additional factor<ref>Often called the ''improvement factor'' or the ''desensitivity factor''.</ref> ( 1 + β (R<sub>L</sub> / R<sub>S</sub> ) A<sub>loaded</sub> ), which is typical of [[negative feedback amplifier]] circuits. The factor β (R<sub>L</sub> / R<sub>S</sub> ) is the current feedback provided by the voltage feedback source of voltage gain β V/V. For instance, for an ideal current source with ''R<sub>S</sub>'' = ∞ Ω, the voltage feedback has no influence, and for ''R<sub>L</sub>'' = 0 Ω, there is zero load voltage, again disabling the feedback. |
| The [[transcendental equation]]s above can be solved exactly in terms of the [[Lambert W function]].
| |
|
| |
|
| ==Output impedance== | | ==References and notes== |
| [[Image:Widlar small-signal.PNG |thumb |350px |Figure 2: Small-signal circuit for finding output resistance of the Widlar source shown in Figure 1. A test current ''I''<sub>x</sub> is applied at the output, and the output resistance is then ''R''<sub>O</sub> = ''V''<sub>x</sub> / ''I''<sub>x</sub>.]]
| | {{reflist|refs= |
| An important property of a current source is its small signal incremental output impedance, which should ideally be infinite. The Widlar circuit introduces local current feedback for transistor <math>Q_{2}</math>. Any increase in the current in ''Q''<sub>2</sub> increases the voltage drop across ''R''<sub>2</sub>, reducing the ''V''<sub>BE</sub> for ''Q''<sub>2</sub>, thereby countering the increase in current. This feedback means the output impedance of the circuit is increased, because the feedback involving ''R''<sub>2</sub> forces use of a larger voltage to drive a given current.
| |
|
| |
|
| Output resistance is found using a small-signal model for the circuit, shown in Figure 2. The transistor ''Q''<sub>1</sub> is replaced by its small-signal emitter resistance ''r''<sub>E</sub> because it is diode connected.<ref name=diode>In a ''diode-connected transistor'' the collector is short-circuited to the base, so the transistor collector-base junction has no time-varying voltage across it. As a result, the transistor behaves like the base-emitter diode, which at low frequencies has a small-signal circuit that is simply the resistor ''r''<sub>E</sub> = ''V''<sub>T</sub> / ''I''<sub>E</sub>, with ''I''<sub>E</sub> the DC [[Q-point]] emitter current. See [[Diode_modelling#Small-signal_modeling|diode small-signal circuit]].</ref> The transistor ''Q''<sub>2</sub> is replaced with its [[hybrid-pi model]]. A test current ''I''<sub>x</sub> is attached at the output.
| | <ref name=H_port>>The [[Two-port network#Hybrid parameters (h-parameters)|h-parameter two port]] is the only two-port among the four standard choices that has a current-controlled current source on the output side.</ref> |
|
| |
|
| Using the figure, the output resistance is determined using Kirchhoff's laws. Using Kirchhoff's voltage law from the ground on the left to the ground connection of ''R''<sub>2</sub>:
| | }} |
| :<math>I_b \left( ( R_1 \parallel r_E ) + r_{\pi} \right) + (I_x + I_b ) R_2 = 0 \ . </math>
| |
| Rearranging:
| |
| :<math>I_b = -I_x \frac{R_2}{( R_1 \parallel r_E ) + r_{\pi} +R_2} \ . </math>
| |
| Using Kirchhoff's voltage law from the ground connection of ''R''<sub>2</sub> to the ground of the test current:
| |
| :<math>V_x=I_x ( r_O +R_2) +I_b (R_2-\beta r_O)\ , </math>
| |
| or, substituting for ''I''<sub>b</sub>:
| |
| | |
| {{anchor|Eq4}}''Eq. 4''
| |
| :<math>R_O = \frac {V_x} {I_x} = r_O \left( 1+ \frac { \beta R_2} {( R_1 \parallel r_E ) + r_{\pi} +R_2} \right) </math>  <math>+ \ R_2 \left( \frac { ( R_1 \parallel r_E ) + r_{\pi}} {( R_1 \parallel r_E ) + r_{\pi} + R_2 } \right) \ . </math>
| |
| | |
| According to ''[[#Eq4|Eq. 4]]'', the output resistance of the Widlar current source is increased over that of the output transistor itself (which is ''r''<sub>O</sub>) so long as ''R''<sub>2</sub> is large enough compared to the ''r''<sub>π</sub> of the output transistor. (Large resistances ''R''<sub>2</sub> make the factor multiplying ''r''<sub>O</sub> approach the value (β +1).) The output transistor carries a low current, making ''r''<sub>π</sub> large, and increase in ''R''<sub>2</sub> tends to reduce this current further, causing a correlated increase in ''r''<sub>π</sub>. Therefore, a goal of ''R''<sub>2</sub> >> ''r''<sub>π</sub> can be unrealistic, and further discussion is provided [[#Current dependence of output resistance|below]]. The resistance ''R''<sub>1</sub>//''r''<sub>E</sub> usually is small because the emitter resistance ''r''<sub>E</sub> usually is only a few ohms.
| |
| | |
| ====Current dependence of output resistance====
| |
| [[Image:Widlar Resistance Plot.PNG|thumb|350px|Figure 3: Design trade-off between output resistance and output current. <font style="font-family: Times New Roman; font-size:110%; font-style:italic; font-weight:normal;"> Top Panel: </font> Circuit output resistance ''R''<sub>O</sub> ''vs.'' DC output current ''I''<sub>C2</sub> using the design formula of ''[[#Eq5|Eq. 5]]'' for ''R''<sub>2</sub> ; <font style="font-family: Times New Roman; font-size:110%; font-style:italic; font-weight:normal;"> Center Panel: </font> Resistance ''R''<sub>O2</sub> in output transistor emitter leg; <font style="font-family: Times New Roman; font-size:110%; font-style:italic; font-weight:normal;"> Bottom Panel: </font> Feedback factor contributing to output resistance. Current in the reference transistor ''Q''<sub>1</sub> is held constant, thereby fixing the compliance voltage. Plots assume ''I''<sub>C1</sub> = 10 mA, ''V''<sub>A</sub> = 50 V, ''V''<sub>CC</sub> = 5 V, ''I''<sub>S</sub> = 10 fA, β<sub>1, 2</sub> = 100 independent of current.]]
| |
| The current dependence of the resistances ''r''<sub>π</sub> and ''r''<sub>O</sub> is discussed in the article [[hybrid-pi model]]. The current dependence of the resistor values is:
| |
| :<math>r_{\pi} = \frac{v_{be}}{i_{b}}\Bigg |_{v_{ce}=0} </math>  <math>=\ \frac{V_\mathrm{T}}{I_\mathrm{B2}} = \beta_2\frac{V_\mathrm{T}}{I_\mathrm{C2}}\ ,</math> in [[Ohm (unit)|ohm]]s, and
| |
| :<math> r_O = \frac{v_{ce}}{i_{c}}\Bigg |_{v_{be}=0} </math>  <math>=\ \frac {V_A}{I_{C2}}</math>   is the output resistance due to the [[Early effect]] when ''V''<sub>CB</sub> = 0 V (device parameter ''V''<sub>A</sub> is the Early voltage).
| |
| From [[#R2|earlier]] in this article (setting the scale currents equal for convenience):
| |
| | |
| {{anchor|Eq5}}''Eq. 5''
| |
| :<math>R_2 = \frac{V_T}{\left(1 + 1/\beta_2 \right) I_{C2}} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math>
| |
| Consequently, for the usual case of small ''r''<sub>E</sub>, and neglecting the second term in ''R''<sub>O</sub> with the expectation that the leading term involving ''r''<sub>O</sub> is much larger:
| |
| | |
| {{Anchor|Eq6}}''Eq. 6''
| |
| :<math>R_O \approx r_O \left( 1+ \frac { \beta_2 R_2} { r_{\pi} +R_2} \right) \ </math> <math>=r_O \left( 1+ \frac { \beta_2\ln \left(\frac {I_{C1}}{I_{C2}}\right)} {\left(\beta_2 + 1 \right) + \ln \left(\frac {I_{C1}}{I_{C2}}\right)} \right) \ , </math>
| |
| | |
| where the last form is found by substituting ''[[#Eq5|Eq. 5]]'' for ''R''<sub>2</sub>. ''[[#Eq6|Eq. 6]]'' shows that a value of output resistance much larger than ''r''<sub>O</sub> of the output transistor results only for designs with ''I''<sub>C1</sub> >> ''I''<sub>C2</sub>. Figure 3 shows that the circuit output resistance ''R''<sub>O</sub> is not determined so much by feedback as by the current dependence of the resistance ''r''<sub>O</sub> of the output transistor. (The output resistance in Figure 3 varies four orders of magnitude, while the feedback factor varies only by one order of magnitude.)
| |
| | |
| Increase of ''I''<sub>C1</sub> to increase the feedback factor also results in increased compliance voltage, not a good thing as that means the current source operates over a more restricted voltage range. So, for example, with a goal for compliance voltage set, placing an upper limit upon ''I''<sub>C1</sub>, and with a goal for output resistance to be met, the maximum value of output current ''I''<sub>C2</sub> is limited.
| |
| | |
| The center panel in Figure 3 shows the design trade-off between emitter leg resistance and the output current: a lower output current requires a larger leg resistor, and hence a larger area for the design. An upper bound on area therefore sets a lower bound on the output current and an upper bound on the circuit output resistance.
| |
| | |
| ''[[#Eq6|Eq. 6]]'' for ''R''<sub>O</sub> depends upon selecting a value of ''R''<sub>2</sub> according to ''[[#Eq5|Eq. 5]]''. That means ''[[#Eq6|Eq. 6]]'' is not a ''circuit behavior'' formula, but a ''design value'' equation. Once ''R''<sub>2</sub> is selected for a particular design objective using ''[[#Eq5|Eq. 5]]'', thereafter its value is fixed. If circuit operation causes currents, voltages or temperatures to deviate from the designed-for values; then to predict changes in ''R''<sub>O</sub> caused by such deviations, ''[[#Eq4|Eq. 4]]'' should be used, not ''[[#Eq6|Eq. 6]]''.
| |
| | |
| ==References==
| |
| <references/>
| |
| ==External links==
| |
| * [http://www.eece.maine.edu/~adelic-i/posters/Group8.pdf Comparison of MOSFET cascode and BJT Widlar current source (PDF)]
| |
| | |
| ==See also==
| |
| *[[Current source]]
| |
| *[[Current mirror]]
| |
| *[[Wilson current source]]
| |
| | |
| ==Further reading==
| |
| *{{cite book |title=Current Sources and Voltage References: A Design Reference for Electronics Engineers|author=Linden T. Harrison |publisher= Elsevier-Newnes |year=2005 |isbn= 075067752X |url=http://books.google.com/books?id=03JmxpE39N4C&printsec=frontcover}}
| |
| *{{cite book |title=Microelectronics: Analysis and Design |author=Sundaram Natarajan |page=319 |url=http://books.google.com/books?id=92LWHJjKcvgC&pg=PA320&lpg=PA320&dq=+%22Widlar+current+source%22&source=web&ots=LFTLwCgje-&sig=SD701CnYP4jRvNigdN9uGYetYqQ&hl=en&sa=X&oi=book_result&resnum=6&ct=result#PPA319,M1
| |
| |isbn=0070590966 |publisher=Tata McGraw-Hill |year=2005 }}
| |
| *[http://sync.cn.nctu.edu.tw/mhcheng/analog-ic/Chap6.pdf Current mirrors and active loads: Mu-Huo Cheng]
| |
| [[Category:Analog circuits]]
| |
| [[Category:Electronic design]]
| |
| [[Category:Electronics terms]]
| |
The account of this former contributor was not re-activated after the server upgrade of March 2022.

Figure 1: Schematic of an electrical circuit illustrating current division. Notation
RT. refers to the
total resistance of the circuit to the right of resistor
RX.
In electronics, a current divider is a simple linear circuit that produces an output current (IX) that is a fraction of its input current (IT). The splitting of current between the branches of the divider is called current division. The currents in the various branches of such a circuit divide in such a way as to minimize the total energy expended.
The formula describing a current divider is similar in form to that for the voltage divider. However, the ratio describing current division places the impedance of the unconsidered branches in the numerator, unlike voltage division where the considered impedance is in the numerator. To be specific, if two or more impedances are in parallel, the current that enters the combination will be split between them in inverse proportion to their impedances (according to Ohm's law). It also follows that if the impedances have the same value the current is split equally.
Resistive divider
A general formula for the current IX in a resistor RX that is in parallel with a combination of other resistors of total resistance RT is (see Figure 1):

where IT is the total current entering the combined network of RX in parallel with RT. Notice that when RT is composed of a parallel combination of resistors, say R1, R2, ... etc., then the reciprocal of each resistor must be added to find the total resistance RT:

General case
Although the resistive divider is most common, the current divider may be made of frequency dependent impedances. In the general case the current IX is given by:

Using Admittance
Instead of using impedances, the current divider rule can be applied just like the voltage divider rule if admittance (the inverse of impedance) is used.

Take care to note that YTotal is a straightforward addition, not the sum of the inverses inverted (as you would do for a standard parallel resistive network). For Figure 1, the current IX would be

Example: RC combination
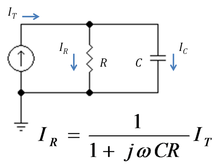
Figure 2: A low pass RC current divider
Figure 2 shows a simple current divider made up of a capacitor and a resistor. Using the formula above, the current in the resistor is given by:


where ZC = 1/(jωC) is the impedance of the capacitor.
The product τ = CR is known as the time constant of the circuit, and the frequency for which ωCR = 1 is called the corner frequency of the circuit. Because the capacitor has zero impedance at high frequencies and infinite impedance at low frequencies, the current in the resistor remains at its DC value IT for frequencies up to the corner frequency, whereupon it drops toward zero for higher frequencies as the capacitor effectively short-circuits the resistor. In other words, the current divider is a low pass filter for current in the resistor.
Loading effect
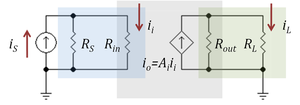
Figure 3: A current amplifier (gray box) driven by a Norton source (
iS,
RS) and with a resistor load
RL. Current divider in blue box at input (
RS,
Rin) reduces the current gain, as does the current divider in green box at the output (
Rout,
RL)
The gain of an amplifier generally depends on its source and load terminations. Current amplifiers and transconductance amplifiers are characterized by a short-circuit output condition, and current amplifiers and transresistance amplifiers are characterized using ideal infinite impedance current sources. When an amplifier is terminated by a finite, non-zero termination, and/or driven by a non-ideal source, the effective gain is reduced due to the loading effect at the output and/or the input, which can be understood in terms of current division.
Figure 3 shows a current amplifier example. The amplifier (gray box) has input resistance Rin and output resistance Rout and an ideal current gain Ai. With an ideal current driver (infinite Norton resistance) all the source current iS becomes input current to the amplifier. However, for a Norton driver a current divider is formed at the input that reduces the input current to

which clearly is less than iS. Likewise, for a short circuit at the output, the amplifier delivers an output current io = Ai ii to the short-circuit. However, when the load is a non-zero resistor RL, the current delivered to the load is reduced by current division to the value:

Combining these results, the ideal current gain Ai realized with an ideal driver and a short-circuit load is reduced to the loaded gain Aloaded:


The resistor ratios in the above expression are called the loading factors. For more discussion of loading in other amplifier types, see loading effect.
Unilateral versus bilateral amplifiers
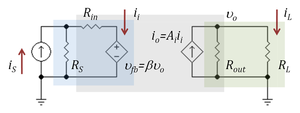
Figure 4: Current amplifier as a bilateral two-port network; feedback through dependent voltage source of gain β V/V
Figure 3 and the associated discussion refers to a unilateral amplifier. In a more general case where the amplifier is represented by a two port, the input resistance of the amplifier depends on its load, and the output resistance on the source impedance. The loading factors in these cases must employ the true amplifier impedances including these bilateral effects. For example, taking the unilateral current amplifier of Figure 3, the corresponding bilateral two-port network is shown in Figure 4 based upon h-parameters.[1] Carrying out the analysis for this circuit, the current gain with feedback Afb is found to be

That is, the ideal current gain Ai is reduced not only by the loading factors, but due to the bilateral nature of the two-port by an additional factor[2] ( 1 + β (RL / RS ) Aloaded ), which is typical of negative feedback amplifier circuits. The factor β (RL / RS ) is the current feedback provided by the voltage feedback source of voltage gain β V/V. For instance, for an ideal current source with RS = ∞ Ω, the voltage feedback has no influence, and for RL = 0 Ω, there is zero load voltage, again disabling the feedback.
References and notes
- ↑ >The h-parameter two port is the only two-port among the four standard choices that has a current-controlled current source on the output side.
- ↑ Often called the improvement factor or the desensitivity factor.















