Venn diagram: Difference between revisions
imported>John R. Brews (More complicated cases) |
imported>John R. Brews m (→Multiple sets) |
||
| Line 40: | Line 40: | ||
The various possible subsets of three sets ''X'', ''Y'' and ''Z'' are shown in the left-hand figure as numbered spaces. For example, the area labeled ‘1’ is the subset of all points that are in ''X'' but in neither ''Y'' nor ''Z''. The subset labeled ‘3’ is the set of all points common to all of ''X'', ''Y'' and ''Z''. Every conceivable arrangement of inclusion and exclusion from any combination of ''X'', ''Y'' and ''Z'' is numbered in the diagram. | The various possible subsets of three sets ''X'', ''Y'' and ''Z'' are shown in the left-hand figure as numbered spaces. For example, the area labeled ‘1’ is the subset of all points that are in ''X'' but in neither ''Y'' nor ''Z''. The subset labeled ‘3’ is the set of all points common to all of ''X'', ''Y'' and ''Z''. Every conceivable arrangement of inclusion and exclusion from any combination of ''X'', ''Y'' and ''Z'' is numbered in the diagram. | ||
The use of circles cannot be extended to more than three sets, however, because insufficient regions can be created to house all the possibilities for subsets. For four sets, ellipses can be used as shown in the figure at right. The numbers correspond to the figure for three sets, but the extra subsets related to set ''W'' have not been numbered. For example, as before, the subset labeled ‘3’ is the set of all points common to all of ''X'', ''Y'' and ''Z''. The asterisk ‘*’ labels the subset of all points common to all four sets ''X'', ''Y'', ''Z'', and ''W''. | The use of circles cannot be extended to more than three sets, however, because insufficient regions can be created to house all the possibilities for subsets. For four sets, ellipses can be used as shown in the figure at right. The numbers correspond to the figure for three sets, but the extra subsets related to set ''W'' have not been numbered. For example, as before, the subset labeled ‘3’ is the set of all points common to all of ''X'', ''Y'' and ''Z'', but not in ''W''. The asterisk ‘*’ labels the subset of all points common to all four sets ''X'', ''Y'', ''Z'', and ''W''. | ||
As the number of sets increases, the Venn diagrams become complicated and hard to follow, the curves become more distorted, and a simple visualization becomes difficult, or perhaps impossible, to achieve. | As the number of sets increases, the Venn diagrams become complicated and hard to follow, the curves become more distorted, and a simple visualization becomes difficult, or perhaps impossible, to achieve. | ||
Revision as of 23:34, 11 July 2011
A Venn diagram is a visualization of logical concepts and propositions using arrangements of intersecting closed curves in a plane.
History
The use of Venn diagrams was introduced by John Venn (1834-1923).[1] A brief biography is found in Hurley.[2]
Examples using two sets
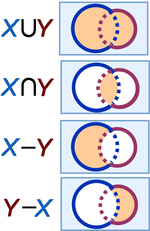
Suppose X and Y are sets, for example, collections of some description. Various operations allow us to build new sets from them, and these definitions are illustrated using the three Venn diagrams in the figure.[3] If we assume the rims contain no points, the figure is straightforward. However, some minutiae arise if the rims are considered to be additional sets with points of their own. These details are described in a footnote.[4]
Union
The union of X and Y, written X∪Y, contains all the elements in X and all those in Y.
Intersection
The intersection of X and Y, written X∩Y, contains all the elements that are common to both X and Y.
Difference
The difference X minus Y, written X−Y or X\Y, contains all those elements in X that are not also in Y.
Complement and universal set
The universal set (if it exists), usually denoted U, is a set of which everything under discussion is a member. In pure set theory, normally sets are the only objects considered. In that case, U would be the set of all sets. However, one may also consider sets that are collections of numbers, or colors, or books, for example; see Set (mathematics).
In the presence of a universal set we can define X′, the complement of X, to be U−X. Set X′ contains everything in the universe apart from the elements of X.
Multiple sets
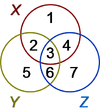
The various possible subsets of three sets X, Y and Z are shown in the left-hand figure as numbered spaces. For example, the area labeled ‘1’ is the subset of all points that are in X but in neither Y nor Z. The subset labeled ‘3’ is the set of all points common to all of X, Y and Z. Every conceivable arrangement of inclusion and exclusion from any combination of X, Y and Z is numbered in the diagram.
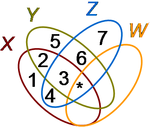
The use of circles cannot be extended to more than three sets, however, because insufficient regions can be created to house all the possibilities for subsets. For four sets, ellipses can be used as shown in the figure at right. The numbers correspond to the figure for three sets, but the extra subsets related to set W have not been numbered. For example, as before, the subset labeled ‘3’ is the set of all points common to all of X, Y and Z, but not in W. The asterisk ‘*’ labels the subset of all points common to all four sets X, Y, Z, and W.
As the number of sets increases, the Venn diagrams become complicated and hard to follow, the curves become more distorted, and a simple visualization becomes difficult, or perhaps impossible, to achieve.
References
- ↑ John Venn (1883). "On the employment of geometrical diagrams for the sensible representation of logical propositions". Proceedings of the Cambridge Philosophical Society: Mathematical and physical sciences 4: pp. 47 ff. and also John Venn (1881). “Chapter V: Diagrammatic representation”, Symbolic logic. Macmillan, pp. 100 ff. Symbolic Logic available also from Chelsea Pub. Co. ISBN 0828402515 (1979) and from the American Mathematical Society ISBN 0821841998 (2006).
- ↑ Patrick J. Hurley (2007). “Eminent logicians: John Venn”, A concise introduction to logic, 10th ed. Cengage learning, p. 252. ISBN 0495503835.
- ↑ Alan Garnham, Jane Oakhill (1994). “§6.2.3b: Venn diagrams”, Thinking and reasoning. Wiley-Blackwell, pp. 105 ff. ISBN 0631170030.
- ↑ If we suppose the perimeters of the circles to contain no points, no complication occurs. If, on the other hand, we consider them to have non-zero width, the figure contains four sets (besides the universal set), set X (white) of points interior to the blue circle, set Y (also white) of points interior to the red circle, set RimX (blue) and set RimY (red). These sets are not disjoint when the two circles overlap, for example, as they do in the figure. In cases of overlap such as the depicted union X∪Y, the red rim enters the interior of the blue circle. Hence, those points in set RimY that are also inside the blue circle are also in set X. They have dual identity, and can be taken either as red or as white points. The figure shows points in the designated union X∪Y as orange. It includes all points in X or in Y or in both, and thus includes the ambiguous, dual-identity points of set RimY. Accordingly, these dual-identity points are part of the union X∪Y and, to make this point, the spaces in the dashed part of the perimeter are colored orange, as are all the points in the union. Likewise for the dual-identity points of set RimX that are part of X∪Y. In set X−Y of the third panel, as a different example, the spaces in the dashed perimeters are colored to show their dual identities as well: the dashed perimeter portion of blue set RimX is also part of set Y as shown by white spaces. Likewise, the dashed part of red set RimY also is part of set X, and hence also part of set X−Y as shown by the orange-colored spaces.
Note: CZ:List-defined references methodology is used for references here.