Venn diagram: Difference between revisions
imported>John R. Brews m (→Examples: link) |
imported>John R. Brews m (→Examples) |
||
| Line 5: | Line 5: | ||
==Examples== | ==Examples== | ||
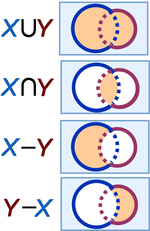
Suppose X and Y are [[Set (mathematics)|sets]]. Various operations allow us to build new sets from them, and these definitions are illustrated using the three Venn diagrams in the figure.<ref name=Oakhill/> | Suppose X and Y are [[Set (mathematics)|sets]], for example, collections of some description. Various operations allow us to build new sets from them, and these definitions are illustrated using the three Venn diagrams in the figure.<ref name=Oakhill/> | ||
==== Union ==== | ==== Union ==== | ||
Revision as of 12:19, 4 July 2011
A Venn diagram is an arrangement of intersecting circles used to visually represent logical concepts and propositions.
Examples
Suppose X and Y are sets, for example, collections of some description. Various operations allow us to build new sets from them, and these definitions are illustrated using the three Venn diagrams in the figure.[1]
Union
The union of X and Y, written X∪Y, contains all the elements in X and all those in Y.
Intersection
The intersection of X and Y, written X∩Y, contains all the elements that are common to both X and Y.
Set difference
The difference X minus Y, written X−Y or X\Y, contains all those elements in X that are not also in Y.
Complement and universal set
The universal set (if it exists), usually denoted U, is a set of which everything under discussion is a member. In pure set theory, normally sets are the only objects considered. In that case, U would be the set of all sets. However, one may also consider sets that are collections of numbers, or colors, or books, for example; see Set (mathematics).
In the presence of a universal set we can define X′, the complement of X, to be U−X. X′ it contains everything in the universe apart from the elements of X.
References
- ↑ Alan Garnham, Jane Oakhill (1994). “§6.2.3b: Venn diagrams”, Thinking and reasoning. Wiley-Blackwell, pp. 105 ff. ISBN 0631170030.