Venn diagram: Difference between revisions
imported>John R. Brews m (add to caption) |
imported>John R. Brews (Add a footnote about finite-width rims) |
||
| Line 11: | Line 11: | ||
--> | --> | ||
==Examples== | ==Examples== | ||
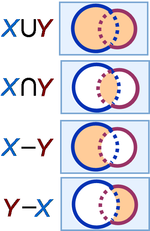
Suppose X and Y are [[Set (mathematics)|sets]], for example, collections of some description. Various operations allow us to build new sets from them, and these definitions are illustrated using the three Venn diagrams in the figure.<ref name=Oakhill/> | Suppose X and Y are [[Set (mathematics)|sets]], for example, collections of some description. Various operations allow us to build new sets from them, and these definitions are illustrated using the three Venn diagrams in the figure.<ref name=Oakhill/> Although the figure is straightforward if we assume the rims are infinitely thin and contain ''no'' points, the figure is straightforward. However, some fine points about these figures arise if the rims are considered to be additional sets with points of their own. These details are described in a footnote.<ref name=details/> | ||
==== Union ==== | ==== Union ==== | ||
| Line 37: | Line 37: | ||
{{Reflist|refs= | {{Reflist|refs= | ||
<ref name=details> | |||
If we suppose the perimeters of the circles to be of zero width, that is, to contain ''no'' points, no complication occurs. If, on the other hand, we consider them to have finite width, the figure contains ''four'' sets (besides the universal set), set ''A'' (white) of points interior to the blue circle, set ''B'' (also white) of points interior to the red circle, set ''RimA'' (blue) and set ''RimB'' (red). These sets are not disjoint when the two circles overlap, for example, as they do in the figure. In cases of overlap such as the depicted union ''A∪B'', the red rim enters the interior of the blue circle. Hence, those points in set ''RimB'' that are also inside the blue circle are also in set ''A''. They have dual identity, and can be taken either as red or as white points. The figure shows points in the designated sets in orange. The union ''A∪B'' includes all points in ''A'' or in ''B'' or in both, and thus includes the ambiguous, dual-identity points of set ''RimB''. Accordingly, these dual-identity points are part of the union ''A∪B'' and are colored orange, as are all the points in the union. Likewise for the dual-identity points of set ''RimA'' that are part of ''A∪B''. | |||
</ref> | |||
<ref name=Hurley> | <ref name=Hurley> | ||
{{cite book |title=A concise introduction to logic |author=Patrick J. Hurley |chapter=Eminent logicians: John Venn |url=http://books.google.com/books?id=XzWWcritSFoC&pg=PT278 |isbn=0495503835 |pages=p. 252 |publisher=Cengage learning |year=2007 |edition=10th ed}} | {{cite book |title=A concise introduction to logic |author=Patrick J. Hurley |chapter=Eminent logicians: John Venn |url=http://books.google.com/books?id=XzWWcritSFoC&pg=PT278 |isbn=0495503835 |pages=p. 252 |publisher=Cengage learning |year=2007 |edition=10th ed}} | ||
Revision as of 09:50, 11 July 2011
A Venn diagram is an arrangement of intersecting circles used to visually represent logical concepts and propositions.
Examples
Suppose X and Y are sets, for example, collections of some description. Various operations allow us to build new sets from them, and these definitions are illustrated using the three Venn diagrams in the figure.[1] Although the figure is straightforward if we assume the rims are infinitely thin and contain no points, the figure is straightforward. However, some fine points about these figures arise if the rims are considered to be additional sets with points of their own. These details are described in a footnote.[2]
Union
The union of X and Y, written X∪Y, contains all the elements in X and all those in Y.
Intersection
The intersection of X and Y, written X∩Y, contains all the elements that are common to both X and Y.
Set difference
The difference X minus Y, written X−Y or X\Y, contains all those elements in X that are not also in Y.
Complement and universal set
The universal set (if it exists), usually denoted U, is a set of which everything under discussion is a member. In pure set theory, normally sets are the only objects considered. In that case, U would be the set of all sets. However, one may also consider sets that are collections of numbers, or colors, or books, for example; see Set (mathematics).
In the presence of a universal set we can define X′, the complement of X, to be U−X. Set X′ contains everything in the universe apart from the elements of X.
History
The use of Venn diagrams was introduced by John Venn (1834-1923).[3] A brief biography is found in Hurley.[4]
References
- ↑ Alan Garnham, Jane Oakhill (1994). “§6.2.3b: Venn diagrams”, Thinking and reasoning. Wiley-Blackwell, pp. 105 ff. ISBN 0631170030.
- ↑ If we suppose the perimeters of the circles to be of zero width, that is, to contain no points, no complication occurs. If, on the other hand, we consider them to have finite width, the figure contains four sets (besides the universal set), set A (white) of points interior to the blue circle, set B (also white) of points interior to the red circle, set RimA (blue) and set RimB (red). These sets are not disjoint when the two circles overlap, for example, as they do in the figure. In cases of overlap such as the depicted union A∪B, the red rim enters the interior of the blue circle. Hence, those points in set RimB that are also inside the blue circle are also in set A. They have dual identity, and can be taken either as red or as white points. The figure shows points in the designated sets in orange. The union A∪B includes all points in A or in B or in both, and thus includes the ambiguous, dual-identity points of set RimB. Accordingly, these dual-identity points are part of the union A∪B and are colored orange, as are all the points in the union. Likewise for the dual-identity points of set RimA that are part of A∪B.
- ↑ John Venn (1883). "On the employment of geometrical diagrams for the sensible representation of logical propositions". Proceedings of the Cambridge Philosophical Society: Mathematical and physical sciences 4: pp. 47 ff. and also John Venn (1881). “Chapter V: Diagrammatic representation”, Symbolic logic. Macmillan, pp. 100 ff. Symbolic Logic available also from Chelsea Pub. Co. ISBN 0828402515 (1979) and from the American Mathematical Society ISBN 0821841998 (2006).
- ↑ Patrick J. Hurley (2007). “Eminent logicians: John Venn”, A concise introduction to logic, 10th ed. Cengage learning, p. 252. ISBN 0495503835.
Note: CZ:List-defined references methodology is used for references here.