User talk:Paul Wormer/scratchbook: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
The '''second law of thermodynamics''', as formulated in the middle of the 19th century by [[William Thomson]] (Lord Kelvin) and [[Rudolf Clausius]], states that it is impossible to gain mechanical energy | The '''second law of thermodynamics''', as formulated in the middle of the 19th century by [[William Thomson]] (Lord Kelvin) and [[Rudolf Clausius]], states that it is impossible to gain mechanical energy from a flow of heat that is directed from a ''cold'' to a ''warm'' body. The law states that the opposite is the case, it requires input of mechanical energy (work) to transport heat from a low- to a high-temperature heat bath. | ||
If the second law would | If the second law would not hold, there would be no energy shortage. For example, it would be possible—as already pointed out by Lord Kelvin—to fuel ships by energy extracted from sea water. After all, the oceans contain immense amounts of [[internal energy]]. When it would be possible to extract a small portion of this energy—whereby a slight cooling of the sea water would occur—and to use this energy to move the ship (a form of work), then the seas could be sailed without any net consumption of energy. It would ''not'' violate the [[first law of thermodynamics]], because the ship's rotating propellers would again heat the water and in total the energy of the supersystem "ship-plus-ocean" would be conserved, in agreement with the first law. Unfortunately, this process is not possible, because ships are warmer than sea water (or at least they are not colder) and hence no work can be extracted from heat flowing from the water to the ship. | ||
==Entropy== | ==Entropy== | ||
Clausius was able to give a mathematical expression of the second law. In order to be able do that, he needed the concept of [[entropy]]. Following his footsteps entropy will be introduced in this subsection. | Clausius was able to give a mathematical expression of the second law. In order to be able do that, he needed the concept of [[entropy]]. Following in his footsteps entropy will be introduced in this subsection. | ||
The state of a | The state of a [[thermodynamic system]] (a point in state space) is characterized by a number of variables, such as [[pressure]] ''p'', [[temperature]] ''T'', amount of substance ''n'', volume ''V'', etc. Any thermodynamic variable can be seen as a function of an arbitrary independent set of other thermodynamic variables, hence the terms "thermodynamic variable" and "thermodynamic function" are used interchangeably. The maximum number of independent variables is equal to the number of energy contacts of the system with its surroundings. When in addition one or more equations of state are assumed to be operative, the number of independent variables is reduced accordingly. For instance, if a gas is assumed to be a Van der Waals gas, i.e., to satisfy the [[Van der Waals equation]] of state, (''p'' + ''a''/''V''<sup>2</sup>)(''V''-''b'') = ''RT'', then this equation between the state variables ''p'' ,''V'', and ''T'' reduces the number of independent variables by one. | ||
A standard example of an energy contact is offered by the prototype thermodynamical system, a gas-filled cylinder with piston. Such a cylinder can perform work | |||
:<math> | :<math> | ||
V_2 | DW = pdV, \quad dV > 0, | ||
= | </math> | ||
on its surroundings, where ''dV'' stands for a small increment of the volume ''V'' of the cylinder, ''p'' is the pressure inside the cylinder and ''DW'' stands for a small amount of work. Work by expansion is a form of energy contact between the cylinder and its surroundings. The small amount of work is indicated by ''D'', and not by ''d'', because ''DW'' is not necessarily a differential of a function. However, when we divide ''DW'' by ''p'' the quantity ''DW''/''p'' becomes obviously equal to the differential ''dV'' of the differentiable state function ''V''. State functions depend only on the actual values of the thermodynamic parameters (they are local), and ''not'' on the path along which the state was reached (the history of the state). Mathematically this means that integration from point 1 to point 2 along path I in state space is equal to integration along another path II, | |||
:<math> | |||
V_2 - V_1 = {\int\limits_1\limits^2}_{{\!\!}^{(I)}} dV | |||
= {\int\limits_1\limits^2}_{{\!\!}^{(II)}} dV | |||
\;\Longrightarrow\; {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DW}{p} = | \;\Longrightarrow\; {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DW}{p} = | ||
{\int\limits_1\limits^2}_{{\!\!}^{(II)}} \frac{DW}{p} | {\int\limits_1\limits^2}_{{\!\!}^{(II)}} \frac{DW}{p} | ||
</math> | </math> | ||
The amount of work (divided by ''p'') performed along path I is equal to the amount of work (divided by ''p'') along path II | The amount of work (divided by ''p'') performed along path I is equal to the amount of work (divided by ''p'') along path II. This condition is necessary and sufficient that ''DW''/''p'' is a state variable. So, although ''DW'' is not a differential, the quotient ''DW''/''p'' is one. | ||
Absorption of a small amount of heat ''DQ'' is another energy contact of | Absorption of a small amount of heat ''DQ'' is another energy contact of a system with its surroundings; ''DQ'' is again not a differential of a certain function. In a completely analogous manner to ''DW''/''p'', the following result can be shown for the heat ''DQ'' (divided by ''T'') absorbed by the system along two different paths: | ||
<div style="text-align: right;" > | <div style="text-align: right;" > | ||
<div style="float: left; margin-left: 35px;" > | <div style="float: left; margin-left: 35px;" > | ||
<math>{\int\limits_1\limits^2}_{{\!\!}^{(I)}}\frac{DQ}{T} = {\int\limits_1\limits^2}_{{\!\!}^{(II)}} \frac{DQ}{T} | <math>{\int\limits_1\limits^2}_{{\!\!}^{(I)}}\frac{DQ}{T} = {\int\limits_1\limits^2}_{{\!\!}^{(II)}} \frac{DQ}{T} . | ||
</math> | </math> | ||
</div> | </div> | ||
| Line 38: | Line 44: | ||
</math> | </math> | ||
(For convenience sake only a single work term was considered here, namely ''DW'' = ''pdV''). | (For convenience sake only a single work term was considered here, namely ''DW'' = ''pdV''). | ||
The internal energy is an extensive quantity, that is, when the system is | The internal energy is an extensive quantity, that is, when the system is doubled, ''U'' is doubled too. The temperature ''T'' is an intensive property, independent of the size of the system. The entropy ''S'', then, is also extensive. In that sense the entropy resembles the volume of the system. | ||
An important difference between ''V'' and ''S'' is that the former is a state function with a well-defined mechanical meaning, whereas entropy is introduced by analogy and is not easily visualized. Indeed, as is shown in the next subsection, it requires a fairly elaborate reasoning to prove that ''S'' is a state function, i.e., equation [[#(1)|(1)]] to hold. | |||
===Proof that entropy is a state | ===Proof that entropy is a state function=== | ||
When equation [[#(1)|(1)]] has been proven, the entropy ''S'' is shown to be a state function. The standard proof, as given now, is physical, by means of [[Carnot cycle]]s, and is based on the Clausius/Kelvin formulation of the second law given in the introduction. | |||
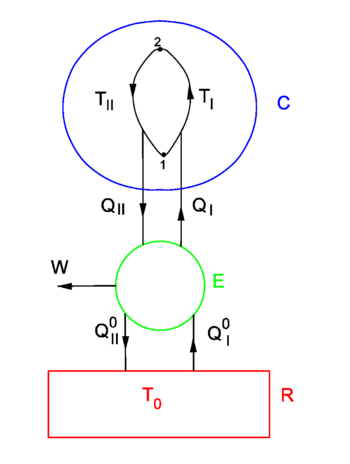
{{Image|Entropy.png|right|350px|Fig. 1. ''T'' > ''T''<sub>0</sub>. (I): Carnot engine E moves heat from heat reservoir R to condensor C and needs input of work DW<sub>in</sub>. (II): E generates work DW<sub>out</sub> from the heat flow from C to R. }} An alternative, more mathematical proof, postulates the existence of a state variable ''S'' with certain properties and derives the existence of [[thermodynamical temperature]] and the second law from these properties. | {{Image|Entropy.png|right|350px|Fig. 1. ''T'' > ''T''<sub>0</sub>. (I): Carnot engine E moves heat from heat reservoir R to condensor C and needs input of work DW<sub>in</sub>. (II): E generates work DW<sub>out</sub> from the heat flow from C to R. }} An alternative, more mathematical proof, postulates the existence of a state variable ''S'' with certain properties and derives the existence of [[thermodynamical temperature]] and the second law from these properties. | ||
In figure 1 a finite heat bath C ("condensor") of constant volume and variable temperature ''T'' is shown. It is connected to an infinite heat reservoir R through a reversible Carnot engine E. Because R is infinite its temperature ''T''<sub>0</sub> is constant, addition or extraction of heat does not change ''T''<sub>0</sub>. It is assumed that always ''T'' ≥ ''T''<sub>0</sub>. One may think of the system E-plus-C as a ship and the heat reservoir R as the sea. The following argument then deals with an attempt of extracting energy from the sea in order to move the ship, i.e., with an attempt to let E perform net outgoing work. | In figure 1 a finite heat bath C ("condensor") of constant volume and variable temperature ''T'' is shown. It is connected to an infinite heat reservoir R through a reversible Carnot engine E. Because R is infinite its temperature ''T''<sub>0</sub> is constant, addition or extraction of heat does not change ''T''<sub>0</sub>. It is assumed that always ''T'' ≥ ''T''<sub>0</sub>. One may think of the system E-plus-C as a ship and the heat reservoir R as the sea. The following argument then deals with an attempt of extracting energy from the sea in order to move the ship, i.e., with an attempt to let E perform net outgoing work in a cyclic (i.e., along a closed path in the state space of C) process. | ||
A Carnot engine performs reversible cycles and per cycle either generates work ''DW''<sub>out</sub> when heat is transported from high temperature to low temperature ( | A Carnot engine performs reversible cycles (in the state space of E, not be confused with cycles in the state space of C) and per cycle either generates work ''DW''<sub>out</sub> when heat is transported from high temperature to low temperature (II), or needs work ''DW''<sub>in</sub> when heat is transported from low to high temperature (I), in accordance with the Clausius/Kelvin formulation of the second law. | ||
The definition of [[thermodynamical temperature]] is such that for | The definition of [[thermodynamical temperature]] is such that for II, | ||
:<math> | :<math> | ||
\frac{DW_\mathrm{out}}{DQ} = \frac{T-T_0}{T}, | \frac{DW_\mathrm{out}}{DQ} = \frac{T-T_0}{T}, | ||
</math> | </math> | ||
while for | while for I | ||
:<math> | :<math> | ||
\frac{DW_\mathrm{in}}{DQ_0} = \frac{T-T_0}{T_0}. | \frac{DW_\mathrm{in}}{DQ_0} = \frac{T-T_0}{T_0}. | ||
</math> | </math> | ||
The first law of thermodynamics states for | The first law of thermodynamics states for I and II, respectively, | ||
:<math> | :<math> | ||
-DW_\mathrm{in} -DQ_0 + DQ=0\quad\hbox{and}\quad DW_\mathrm{out} + DQ_0-DQ=0 | -DW_\mathrm{in} -DQ_0 + DQ=0\quad\hbox{and}\quad DW_\mathrm{out} + DQ_0-DQ=0 | ||
</math> | </math> | ||
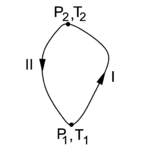
{{Image|Cycle entropy.png|right|150px|Fig. 2. Two paths in the state space of the "condensor" C.}} | {{Image|Cycle entropy.png|right|150px|Fig. 2. Two paths in the state space of the "condensor" C.}} | ||
For | For I, | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 79: | Line 87: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
In figure 2 the state diagram of the "condensor" C is shown. Along path I the Carnot engine needs input of work to transport heat from the reservoir R to C and the absorption of heat raises | In figure 2 the state diagram of the "condensor" C is shown. Along path I the Carnot engine needs input of work to transport heat from the colder reservoir R to the hotter C and the absorption of heat by C raises its temperature and pressure. Integration of ''DW''<sub>in</sub> = ''DQ'' − ''DQ''<sub>0</sub> (that is, summation over many cycles of the engine E) along path I gives | ||
:<math> | :<math> | ||
W_\mathrm{in} = Q_\mathrm{in} - T_0 {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DQ}{T} \quad\hbox{with}\quad Q_\mathrm{in} \equiv {\int\limits_1\limits^2}_{{\!\!}^{(I)}} DQ. | W_\mathrm{in} = Q_\mathrm{in} - T_0 {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DQ}{T} \quad\hbox{with}\quad Q_\mathrm{in} \equiv {\int\limits_1\limits^2}_{{\!\!}^{(I)}} DQ. | ||
</math> | </math> | ||
Along path II the Carnot engine delivers work while transporting heat from C to R. Integration of ''DW''<sub>out</sub> = ''DQ'' − ''DQ''<sub>0</sub> along path | Along path II the Carnot engine delivers work while transporting heat from C to R. Integration of ''DW''<sub>out</sub> = ''DQ'' − ''DQ''<sub>0</sub> along path II gives | ||
:<math> | :<math> | ||
W_\mathrm{out} = Q_\mathrm{out} - T_0 {\int\limits_2\limits^1}_{{\!\!}^{(II)}} \frac{DQ}{T} | W_\mathrm{out} = Q_\mathrm{out} - T_0 {\int\limits_2\limits^1}_{{\!\!}^{(II)}} \frac{DQ}{T} | ||
| Line 89: | Line 97: | ||
</math> | </math> | ||
Assume now that the amount of heat ''Q''<sub>out</sub> extracted (along path II) from C and the heat ''Q''<sub>in</sub> delivered (along I) to C are the same in absolute value | Assume now that the amount of heat ''Q''<sub>out</sub> extracted (along path II) from C and the heat ''Q''<sub>in</sub> delivered (along I) to C are the same in absolute value. In other words, after having gone along a closed path in the state diagram of figure 2, the condensor C has not gained or lost heat. That is, | ||
:<math> | :<math> | ||
Q_\mathrm{in} + Q_\mathrm{out} = 0, \, | Q_\mathrm{in} + Q_\mathrm{out} = 0, \, | ||
</math> | </math> | ||
then | |||
:<math> | :<math> | ||
W_\mathrm{in} + W_\mathrm{out} = - T_0 {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DQ}{T} | W_\mathrm{in} + W_\mathrm{out} = - T_0 {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DQ}{T} | ||
- T_0 {\int\limits_2\limits^1}_{{\!\!}^{(II)}} \frac{DQ}{T}. | - T_0 {\int\limits_2\limits^1}_{{\!\!}^{(II)}} \frac{DQ}{T}. | ||
</math> | </math> | ||
If the total net work ''W''<sub>in</sub> + ''W''<sub>out</sub> | If the total net work ''W''<sub>in</sub> + ''W''<sub>out</sub> is positive (outgoing), this work is done by heat obtained from R, which is not possible because of the Clausius/Kelvin principle. If the total net work ''W''<sub>in</sub> + ''W''<sub>out</sub> is negative, then by inverting all reversible processes, i.e., by going down path I and going up along II, the net work changes sign and becomes positive (outgoing). Again the Clausius/Kelvin principle is violated. The conclusion is that the net work is zero and that | ||
:<math> | :<math> | ||
T_0 {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DQ}{T} + | T_0 {\int\limits_1\limits^2}_{{\!\!}^{(I)}} \frac{DQ}{T} + | ||
Revision as of 05:39, 29 October 2009
The second law of thermodynamics, as formulated in the middle of the 19th century by William Thomson (Lord Kelvin) and Rudolf Clausius, states that it is impossible to gain mechanical energy from a flow of heat that is directed from a cold to a warm body. The law states that the opposite is the case, it requires input of mechanical energy (work) to transport heat from a low- to a high-temperature heat bath.
If the second law would not hold, there would be no energy shortage. For example, it would be possible—as already pointed out by Lord Kelvin—to fuel ships by energy extracted from sea water. After all, the oceans contain immense amounts of internal energy. When it would be possible to extract a small portion of this energy—whereby a slight cooling of the sea water would occur—and to use this energy to move the ship (a form of work), then the seas could be sailed without any net consumption of energy. It would not violate the first law of thermodynamics, because the ship's rotating propellers would again heat the water and in total the energy of the supersystem "ship-plus-ocean" would be conserved, in agreement with the first law. Unfortunately, this process is not possible, because ships are warmer than sea water (or at least they are not colder) and hence no work can be extracted from heat flowing from the water to the ship.
Entropy
Clausius was able to give a mathematical expression of the second law. In order to be able do that, he needed the concept of entropy. Following in his footsteps entropy will be introduced in this subsection.
The state of a thermodynamic system (a point in state space) is characterized by a number of variables, such as pressure p, temperature T, amount of substance n, volume V, etc. Any thermodynamic variable can be seen as a function of an arbitrary independent set of other thermodynamic variables, hence the terms "thermodynamic variable" and "thermodynamic function" are used interchangeably. The maximum number of independent variables is equal to the number of energy contacts of the system with its surroundings. When in addition one or more equations of state are assumed to be operative, the number of independent variables is reduced accordingly. For instance, if a gas is assumed to be a Van der Waals gas, i.e., to satisfy the Van der Waals equation of state, (p + a/V2)(V-b) = RT, then this equation between the state variables p ,V, and T reduces the number of independent variables by one.
A standard example of an energy contact is offered by the prototype thermodynamical system, a gas-filled cylinder with piston. Such a cylinder can perform work
on its surroundings, where dV stands for a small increment of the volume V of the cylinder, p is the pressure inside the cylinder and DW stands for a small amount of work. Work by expansion is a form of energy contact between the cylinder and its surroundings. The small amount of work is indicated by D, and not by d, because DW is not necessarily a differential of a function. However, when we divide DW by p the quantity DW/p becomes obviously equal to the differential dV of the differentiable state function V. State functions depend only on the actual values of the thermodynamic parameters (they are local), and not on the path along which the state was reached (the history of the state). Mathematically this means that integration from point 1 to point 2 along path I in state space is equal to integration along another path II,
The amount of work (divided by p) performed along path I is equal to the amount of work (divided by p) along path II. This condition is necessary and sufficient that DW/p is a state variable. So, although DW is not a differential, the quotient DW/p is one.
Absorption of a small amount of heat DQ is another energy contact of a system with its surroundings; DQ is again not a differential of a certain function. In a completely analogous manner to DW/p, the following result can be shown for the heat DQ (divided by T) absorbed by the system along two different paths:
(1)
Hence the quantity dS defined by
is the differential of a state variable S, the entropy of the system. Before proving equation (1) from the second law, it is emphasized that this definition of entropy only fixes entropy differences:
Note further that entropy has the dimension energy per degree temperature (joule per degree kelvin) and recalling the first law of thermodynamics (the differential dU of the internal energy satisfies dU = DQ + DW), it follows that
(For convenience sake only a single work term was considered here, namely DW = pdV). The internal energy is an extensive quantity, that is, when the system is doubled, U is doubled too. The temperature T is an intensive property, independent of the size of the system. The entropy S, then, is also extensive. In that sense the entropy resembles the volume of the system.
An important difference between V and S is that the former is a state function with a well-defined mechanical meaning, whereas entropy is introduced by analogy and is not easily visualized. Indeed, as is shown in the next subsection, it requires a fairly elaborate reasoning to prove that S is a state function, i.e., equation (1) to hold.
Proof that entropy is a state function
When equation (1) has been proven, the entropy S is shown to be a state function. The standard proof, as given now, is physical, by means of Carnot cycles, and is based on the Clausius/Kelvin formulation of the second law given in the introduction.
An alternative, more mathematical proof, postulates the existence of a state variable S with certain properties and derives the existence of thermodynamical temperature and the second law from these properties.
In figure 1 a finite heat bath C ("condensor") of constant volume and variable temperature T is shown. It is connected to an infinite heat reservoir R through a reversible Carnot engine E. Because R is infinite its temperature T0 is constant, addition or extraction of heat does not change T0. It is assumed that always T ≥ T0. One may think of the system E-plus-C as a ship and the heat reservoir R as the sea. The following argument then deals with an attempt of extracting energy from the sea in order to move the ship, i.e., with an attempt to let E perform net outgoing work in a cyclic (i.e., along a closed path in the state space of C) process.
A Carnot engine performs reversible cycles (in the state space of E, not be confused with cycles in the state space of C) and per cycle either generates work DWout when heat is transported from high temperature to low temperature (II), or needs work DWin when heat is transported from low to high temperature (I), in accordance with the Clausius/Kelvin formulation of the second law.
The definition of thermodynamical temperature is such that for II,
while for I
The first law of thermodynamics states for I and II, respectively,
For I,
For II we find the same result,
In figure 2 the state diagram of the "condensor" C is shown. Along path I the Carnot engine needs input of work to transport heat from the colder reservoir R to the hotter C and the absorption of heat by C raises its temperature and pressure. Integration of DWin = DQ − DQ0 (that is, summation over many cycles of the engine E) along path I gives
Along path II the Carnot engine delivers work while transporting heat from C to R. Integration of DWout = DQ − DQ0 along path II gives
Assume now that the amount of heat Qout extracted (along path II) from C and the heat Qin delivered (along I) to C are the same in absolute value. In other words, after having gone along a closed path in the state diagram of figure 2, the condensor C has not gained or lost heat. That is,
then
If the total net work Win + Wout is positive (outgoing), this work is done by heat obtained from R, which is not possible because of the Clausius/Kelvin principle. If the total net work Win + Wout is negative, then by inverting all reversible processes, i.e., by going down path I and going up along II, the net work changes sign and becomes positive (outgoing). Again the Clausius/Kelvin principle is violated. The conclusion is that the net work is zero and that
From this independence of path it is concluded that
is a state (local) variable.